约数专题

《算法竞赛进阶指南》0x32_2约数

定义 ∀ a , b ∈ N , 若 g c d ( a , b ) = 1 , 则称 a ， b 互质 \forall a,b \in \mathbb{N},若gcd(a,b)=1,则称a，b互质 ∀a,b∈N,若gcd(a,b)=1,则称a，b互质。对于三个数或更多个数的情况，我们把 g c d ( a , b , c ) = 1 gcd(a,b,c)=1 gcd(a,b,c)=1的情况称

约数个数a

给定 nn 个正整数 aiai，请你输出这些数的乘积的约数个数，答案对 109+7109+7 取模。输入格式第一行包含整数 nn。接下来 nn 行，每行包含一个整数 aiai。输出格式输出一个整数，表示所给正整数的乘积的约数个数，答案需对 109+7109+7 取模。数据范围 1≤n≤1001≤n≤100, 1≤ai≤2×1091≤ai≤2×109 输入样例： 32

Light OJ 1054 Efficient Pseudo Code 求n^m的约数和

题目来源：Light OJ 1054 Efficient Pseudo Code 题意：求n的m次这个数的所有的约数和思路：首先对于一个数n = p1^a1*p2^a2*p3^a3*…*pk^ak 约束和s = (p1^0+p1^1+p1^2+…p1^a1)(p2^0+p2^1+p2^2+…p2^a2)…(pk^0+pk^1+pk^2+…pk^ak）然后就是先求素数表分解因子然后求

poj 3361 Gaussian Prime Factors 高斯素数约数

poj 3361 Gaussian Prime Factors 题意：在复数 a+bj (a,b为整数)范围内，约数只有 1, -1, a+bj, -(a+bj)的称为高斯素数。求任给正整数N的所有素因子(|b|>a>0)。默认N<2e9 解法：定理有云： n≡3(mod 4)者，无因式分解。 n≡1(mod 4)者，可唯一分解为两个共轭高斯整数乘积。当然做的时候并不知道！

bzoj1968[Ahoi2005] COMMON 约数研究

题目链接：bzoj1968 题目大意：求1到n各个数约数个数的和。 1≤n≤106 1≤n≤10^6 题解： …我怎么这么蠢。一直在想怎么化这个公式： ∑i=1n∑d|n1 \sum_{i=1}^{n}\sum_{d|n}1 ？？？我真搞笑直接for一遍 n n就好了。对于一个数ii，1到 n n中就会有n/in/i个数是它的倍数，即有

约数倍数

#include<stdio.h> main() { int m,n,k,temp,p; scanf("%d%d",&m,&n); if(m<n) { temp=m; m=n; n=temp; } k=m%n; p=m*n; while(k!=0) { m=n; n=k; k=m%n; }

数论学习之约数

最近学数论真的感觉自己脑子很不好用啊，一个证明题想半天。感觉一些基础的知识还是比较重要的，所以就记录下来吧，加深一下印象。对于一个整数n，假如我们想求到这个整数的所有的约数的话，我们只要对其 1 − n 1-\sqrt{n} 1−n 之间找可以被n整除的那些数，然后就可以找到它们的约数了。时间复杂度 O ( n ) O(\sqrt{n}) O(n ). 代码： //试除法int

蓝桥杯刷题-约数的个数

3377. 约数的个数 - AcWing题库 #include <bits/stdc++.h>using namespace std;int n;int Get(int x){int ans = 0;for(int i = 1;i <= x / i; i ++){if(x % i == 0 && i != x / i) ans += 2;if(x % i == 0 && i == x / i

C - Fear Factoring Gym - 101615C（求约数和，除法分块）

Problem C — limit 1 second Fear Factoring The Slivians are afraid of factoring; it’s just, well, difficult. Really, they don’t even care about the factors themselves, just how much they sum to. We can

洛谷P2424 约数和（除法分块）

展开题目背景 Smart最近沉迷于对约数的研究中。题目描述对于一个数X，函数f(X)表示X所有约数的和。例如：f(6)=1+2+3+6=12。对于一个X，Smart可以很快的算出f(X)。现在的问题是，给定两个正整数X,Y(X<Y)，Smart希望尽快地算出f(X)+f(X+1)+……+f(Y)的值，你能帮助Smart算出这个值吗？输入格式输入文件仅一行，两个正整数X和Y（X<Y），

约数与倍数-第12届蓝桥杯选拔赛Python真题精选

[导读]：超平老师的Scratch蓝桥杯真题解读系列在推出之后，受到了广大老师和家长的好评，非常感谢各位的认可和厚爱。作为回馈，超平老师计划推出《Python蓝桥杯真题解析100讲》，这是解读系列的第45讲。约数与倍数，本题是2020年11月21日举办的第12届蓝桥杯青少组Python编程选拔赛真题，题目要求编程计算并输出给定两个正整数的最大公约数和最小公倍数。先来看看题目的要求吧。

蓝桥杯每日一题：约数个数（质因数）

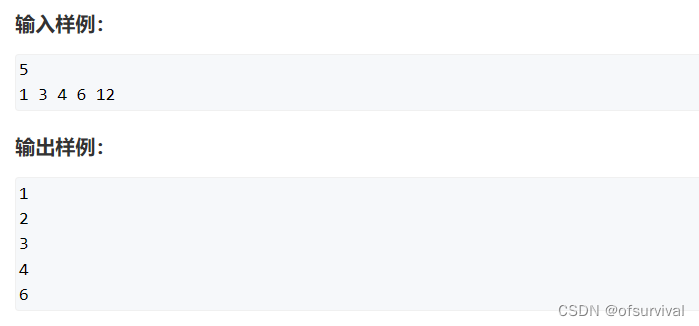
题目描述：输入 n 个整数，依次输出每个数的约数的个数。输入格式第一行包含整数 n。第二行包含 n 个整数 ai。输出格式共 n 行，按顺序每行输出一个给定整数的约数的个数。数据范围 1≤n≤1000, 1≤ai≤10^9 输入样例： 51 3 4 6 12 输出样例： 12346 解题思路： 1.枚举每个数，暴力求取每个数的约数； 2.根据

SVM中的拉格朗日乘子法解决不等式约数问题（KKT）

https://blog.csdn.net/howardemily/article/details/79949646

数学知识--（质数，约数）

本文用于个人算法竞赛学习，仅供参考目录一.质数的判定二.分解质因数三.质数筛 1.朴素筛法 2.埃氏筛法 3.线性筛法四.约数 1.求一个数的所有约数 2.约数个数和约数之和 3.欧几里得算法（辗转相除法）-- 求最大公约数一.质数的判定质数：质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的数。常见的质数有2, 3, 5,

AcWing刷题-约数个数

约数的个数代码 # 计数def f(x)->int:cnt = 0i = 1while i * i <= x:if x % i == 0:cnt += 1if i * i < x:cnt += 1i += 1return cntn = int(input())a = list(map(int,input().split()))for i in a:print(f(i))

算法学习14：数论（质数，约数，欧拉函数，快速幂）

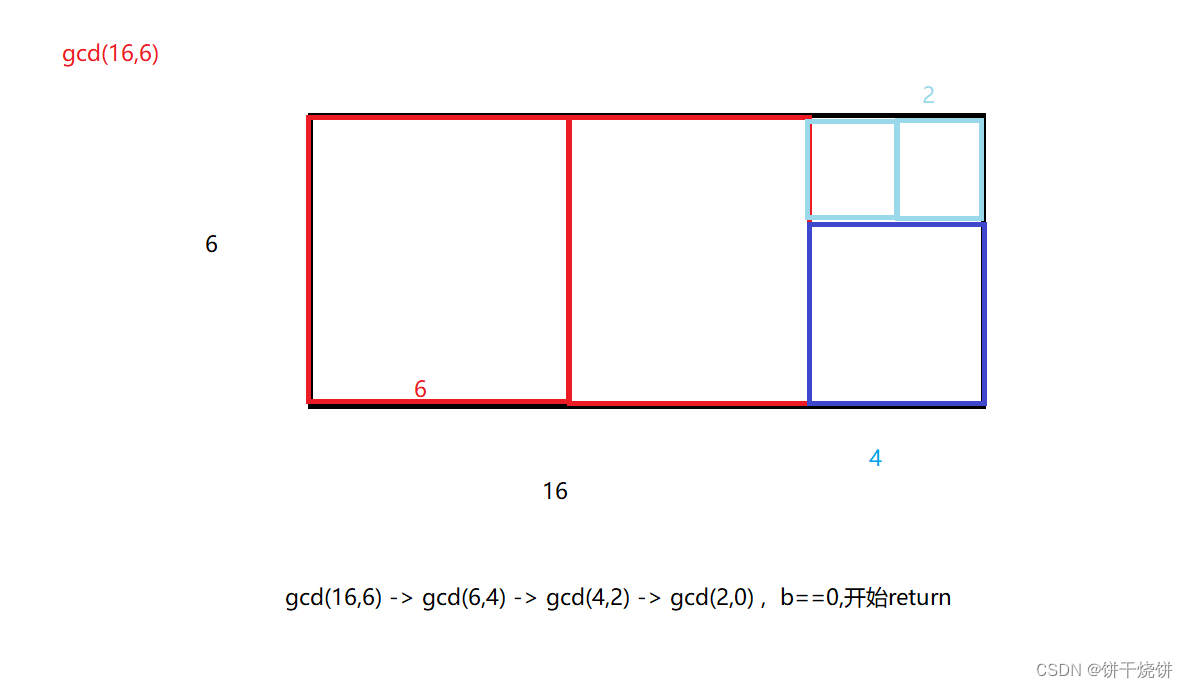
算法学习14：数论（质数，约数，欧拉函数，快速幂）文章目录算法学习14：数论（质数，约数，欧拉函数，快速幂）前言要记忆的模版：一、质数1.质数的判定：试除法2.质因数的分解：试除法3.筛质数：埃氏筛、线性筛二、约数1.试除法求约数2.求约数个数、约数之和（懵懵的）3.辗转相处法求最大公约数（欧几里得定理）4.扩展欧几里得定理：线性同余方程：（和扩展欧几里得定理一样，不太理解，待以

蓝桥杯算法提高ADV-98 约数个数

题目试题算法提高约数个数资源限制时间限制：1.0s 内存限制：512.0MB 　　输入一个正整数N 　　样例输入 12 样例输出 6 样例说明 12的约数包括：1,2,3,4,6,12。共6个 package 蓝桥练习;import java.util.Scanner;/*** 样例说明12的约数包括：1,2,3,4,6,12。共6个*/public class Main {p

NOJ 1203 最多约数问题 (算数基本定理 DFS +剪枝)

最多约数问题时间限制(普通/Java) : 20000 MS/ 30000 MS 运行内存限制 : 81920 KByte 题目描述正整数x的约数是能整除x的正整数。正整数x的约数个数记为div（x）。例如，1,2,5,10都是正整数10的约数，且d

【题解】最大奇约数

题目题目描述定义函数f(x)表示x的最大奇约数，这里x表示正整数。例如，f(20) = 5，因为20的约数从小到大分别有：1, 2, 4, 5, 10, 20，其中最大的奇约数为5。给出正整数N，求f(1)+f(2)+…+f(N) 输入格式第1行：1个正整数N 1<=N<=10^9 样例样例输入 7 样例输出 21 数据范围与提示样例说明 f(1)+f(2

acwing——869. 试除法求约数

869. 试除法求约数给定n个正整数ai，对于每个整数ai,请你按照从小到大的顺序输出它的所有约数。输入格式第一行包含整数n。接下来n行，每行包含一个整数ai。输出格式输出共n行，其中第 i 行输出第 i 个整数ai的所有约数。数据范围 1≤n≤100, 2≤ai≤2∗109 输入样例： 2 6 8 输出样例： 1 2 3 6 1 2 4 8 解题思路：直接从1开始遍

【bzoj1968】【Ahoi2005】【COMMON 约数研究】【循环】

Description Input 只有一行一个整数 N（0 < N < 1000000）。 Output 只有一行输出，为整数M，即f(1)到f(N)的累加和。 Sample Input 3 Sample Output 5 题解：直接枚举每个因子，计算一下会有多少个数含有它，累加进答案即可。。 #include<iostream>#

蓝桥杯算法提高算法提高约数个数

输入一个正整数N (1 样例输入 12 样例输出 6 样例说明 12的约数包括：1,2,3,4,6,12。共6个 #include <stdio.h> #include <math.h> int main() { int n,i,c=0; scanf("%d",&n); for (i=1;i<=n;

SSL 2406 2408 约数比萨

比赛约数题目：求一个数的约数和分析：模拟，注意完全平方数的情况代码： #include <cstdio>#include <cmath>using namespace std;int n,ans;int main(){freopen("bri.in","r",stdin);freopen("bri.out","w",stdout);scanf("%d"

约数个数--数学模板

点击跳转例题一个数分解质因数之后，如果要求出其中某个约数，那么就是这些质因子选与不选，选几个来组合的问题。所以有多少种选法就是简单的乘法原理。核心代码 unordered_map<int,int>mp;for(int i=2;i<=x/i;i++){while(x%i==0)mp[i]++,x/=i;}if(x>1)mp[x]++; 例题代码： #include <bits/stdc+

ACwing求一个数约数个数

给定 n 个正整数 ai，请你输出这些数的乘积的约数个数，答案对 109+7 取模。输入格式第一行包含整数 n。接下来 n 行，每行包含一个整数 ai。输出格式输出一个整数，表示所给正整数的乘积的约数个数，答案需对 109+7 取模。数据范围 1≤n≤100, 1≤ai≤2×109 输入样例： 3268 输出样例： 12 公式：一个数的所有质因子

acwing数学知识（一）质数约数

1.质数——筛质数题目：给定一个正整数n，请你求出1~n中质数的个数。（1）朴素筛法O(nlogn) 算法核心：把每个数的所有倍数筛掉调和级数：1 + 1/2 + 1/3 +…+ 1/n = lnn + c(c欧拉常数=0.577) 算法时间复杂度：最外层遍历整个数组是n（其实不用管，只用看内部总次数即可），内部循环总次数是n/2,n/3,n/4…1，累加得n(1/2 + 1/3