本文主要是介绍约数与倍数-第12届蓝桥杯选拔赛Python真题精选,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第45讲。
约数与倍数,本题是2020年11月21日举办的第12届蓝桥杯青少组Python编程选拔赛真题,题目要求编程计算并输出给定两个正整数的最大公约数和最小公倍数。
先来看看题目的要求吧。
一.题目说明
提示信息:
倍数与约数:如果a能被b整除,a就叫做b的倍数,b就叫做a的约数。约数和倍数都表示一个整数与另一个整数的关系,不能单独存在。
最大公约数:几个整数中公有的约数,叫做这几个数的公约数;其中最大的一个,叫做这几个数的最大公约数。
举例:12、16的公约数有1、2、4,其中最大的一个是4,所以4是12与16的最大公约数。
最小公倍数:几个自然数公有的倍数,叫做这几个数的公倍数,其中最小的一个,叫做这几个数的最小公倍数。
举例:4的倍数有4、8、12、16,….,6的倍数有6、12、18、24,….,4和6的公倍数有12、24,……其中最小的是12,所以4和6最小公倍数为 12。
编程实现:
分别输入两个正整数(1 < 正整数 < 201),输出这两个正整数的最大公约数M及最小公倍数N(注:M和N之间以一个英文逗号隔开)。
输入描述:
第1行输入第一个正整数
第2行输入第二个正整数
输出描述:
输出这两个正整数的最大公数M及最小公倍数N(M和N之间以一个英文逗号隔开)
样例输入:
4
6
样例输出:
2,12
二.思路分析
这是一道简单的数论题,考查的是最大公约数和最小公倍数算法,涉及的知识点包括循环、余数运算和函数。
最大公约数,也称最大公因数、最大公因子,指两个或多个整数共有约数中最大的一个,通常称之为GCD(Greatest Common Divisor)。
例如8和12,两个数的公约数分别为1、2、4,其中4为8和12的最大公约数。
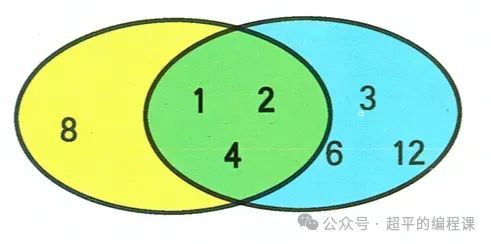
计算最大公约数的方法比较多,常见的有如下几种:
-
枚举算法
-
欧几里得算法
-
更相减损术
-
Stein算法
其中最简单的就是枚举算法,其核心思想就是从较小的数字开始,寻找能同时被两个正整数整除的数字,直到1为止,一旦找到了,就结束循环。
欧几里得算法,又称辗转相除法,是一种高效的求解方法。它的基本思想是用两个数的余数进行迭代计算,直到余数为0时,此时的除数即为两个数的最大公约数。
该算法基于一个定理:
两个正整数a和b( a > b),它们的最大公约数等于a除以b的余数c和b之间的最大公约数。
我们先来看一看数字1112和695的最大公约数是多少吧,使用欧几里得算法的步骤如下:

与最大公约数相对应的概念是最小公倍数,两个或多个整数公有的倍数叫做它们的公倍数,其中除0以外最小的一个公倍数就叫做最小公倍数,通常称之为LCM(Least Common Multiple)。
比如,要计算15和35的最小公倍数,如下所示:

其计算方式也有多种,典型的有两种,第一种是使用枚举算法,第二种是利用最大公约数来计算。
我们可以利用这样一个事实:两个数的乘积等于它们的最大公约数和最小公倍数的乘积,也就是说:
a * b = GCD(a, b) * LCM(a, b)因此,我们可以先计算最大公约数,然后用这个公式来获取最小公倍数。
思路有了,接下来,我们就进入具体的编程实现环节。
三.编程实现
根据上面的思路分析,我们使用两种方式实现:
-
枚举算法
-
欧几里得算法
1. 枚举算法
为了方便,我们可以定义函数来获取两个整数的最大公约数和最小公倍数,计算GCD的函数定义如下:
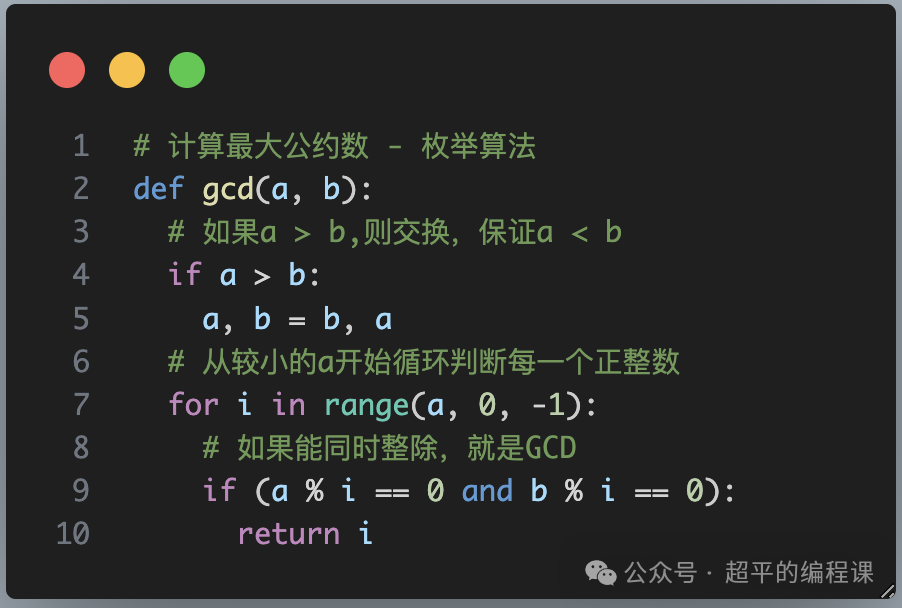
代码不难,简单说明两点:
1). 需要比较a和b的大小,确保 a < b;
2). 注意从较小的a开始,直到1为止,一旦找到第一个公约数,它就是最大的,结束循环,返回即可。
计算LCM的函数定义如下:
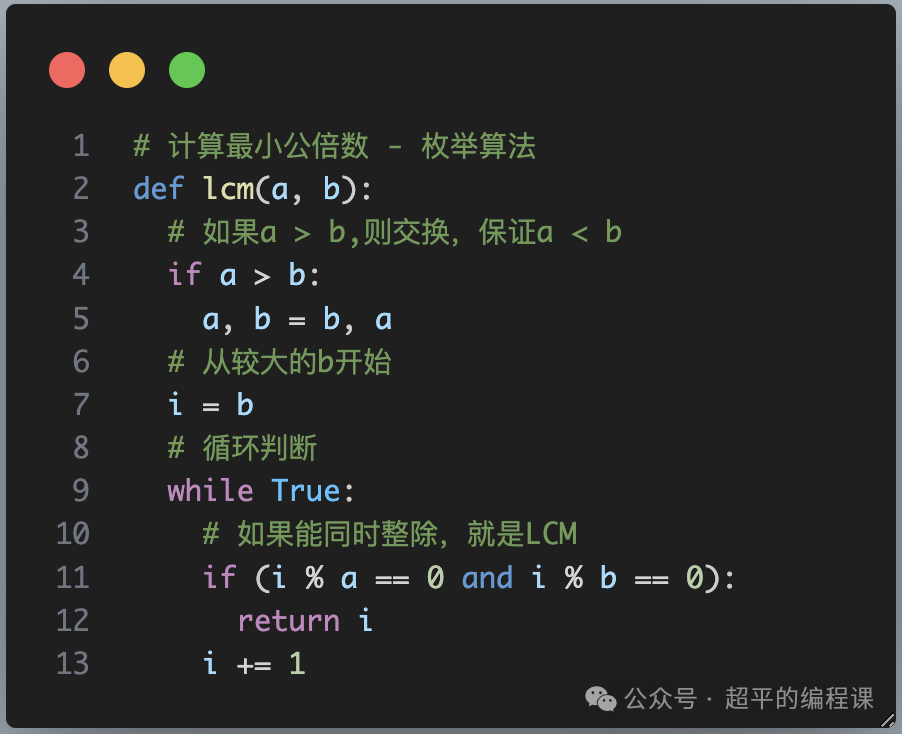
同样说明两点:
1). 仍然要比较a和b的大小,确保a < b;
2). 循环的次数无法确定,不能使用for...in循环,使用while更方便。
2. 欧几里得算法
接下来,我们使用欧几里得算法来计算最大公约数,定义函数如下:

代码不多,强调一点,有些同学会先比较a和b的大小,这是可以的。但实际上不需要比较a和b的大小,因为算法本身会处理这种情况。无论a和b的初始大小关系如何,算法都会正确地计算出它们的最大公约数。
在每一次迭代中,我们将较小的数和较大的数除以较小数后的余数进行交换。由于余数总是小于除数,因此这个过程会确保我们总是用较小的数去除以较大的数,直到余数为0。
相应的,计算最小公倍数的函数定义如下:

代码更为简单,注意使用的是整除运算符,确保得到的结果是整数。
有了前面定义的函数,接下来就简单了,代码如下:

代码非常简单,说明两点:
1). 前面给出了两种算法,你只需要使用其中一种即可;
2). 最后输出的使用,需要使用逗号隔开,使用sep参数最简单,效果也最好。
至此,整个程序就全部完成了,你也可以输入不同的数字来测试效果了。
四.总结与思考
本题代码在10行左右,涉及到的知识点包括:
-
输入输出;
-
循环编程,包括for和while;
-
余数运算;
-
自定义函数;
本题难度一般,关键是要理解最大公约数和最小公倍数的含义,快速找到解决方案。
枚举算法是最简单的,也是我们解决大部分问题的首选,但是随着数字或者数据规模的增加,枚举算法的效率就会大大降低。
以上面的代码为例,假设我们有两个整数a和b(假设a <= b),使用枚举算法来计算它们的最大公约数的复杂度可以这样分析:
在最坏情况下,我们需要尝试从a(较小数)递减到1,检查每个数是否是a和b的公约数,因此,需要进行的比较次数是a次。
所以,枚举算法计算GCD的时间复杂度是O(a)。这个复杂度是线性的,意味着随着输入数a的增大,所需的时间也会线性地增长。
使用欧几里得算法时,我们是通过余数来不断减小数字的,其时间复杂度与a和b中较小者的值成对数关系,即O(log(min(a, b))),这在处理大整数时具有显著的优势。
超平老师给你留一道思考题,除了本文介绍的枚举算法和欧几里得算法,其它几种算法思想是怎样的,又该如何编写代码呢?
你还有什么好的想法和创意吗,也非常欢迎和超平老师分享探讨。
如果你觉得文章对你有帮助,别忘了点赞和转发,予人玫瑰,手有余香😄
需要源码的,可以移步至“超平的编程课”gzh。
这篇关于约数与倍数-第12届蓝桥杯选拔赛Python真题精选的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








