洛谷P2424 约数和（除法分块）

本文主要是介绍洛谷P2424 约数和（除法分块），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

展开
题目背景
Smart最近沉迷于对约数的研究中。

题目描述
对于一个数X，函数f(X)表示X所有约数的和。例如：f(6)=1+2+3+6=12。对于一个X，Smart可以很快的算出f(X)。现在的问题是，给定两个正整数X,Y(X<Y)，Smart希望尽快地算出f(X)+f(X+1)+……+f(Y)的值，你能帮助Smart算出这个值吗？

输入格式
输入文件仅一行，两个正整数X和Y（X<Y），表示需要计算f(X)+f(X+1)+……+f(Y)。

输出格式
输出只有一行，为f(X)+f(X+1)+……+f(Y)的值。

输入输出样例
输入 #1复制
2 4
输出 #1复制
14
输入 #2复制
123 321
输出 #2复制
72543
说明/提示
对于20%的数据有1≤X＜Y≤105。

对于60%的数据有1≤X＜Y≤1*107。

对于100%的数据有1≤X＜Y≤2*109。

思路：
同C - Fear Factoring Gym - 101615C（求约数和，除法分块）

暴力的思路是：对于 i (i ≤ n)，存在n / i个i，和为n / i * i。
除法分块的意思是，n / i 的值对于连续的i都是确定的，而且这个连续i的右边界为n / (n / i)。
那么对于这个连续的范围，约数是等差递增的，而且数目是相同的。
结果就是等差数列求和再乘上数目。
等差数列求和为 (l + r) * (r - l + 1) * n / i.

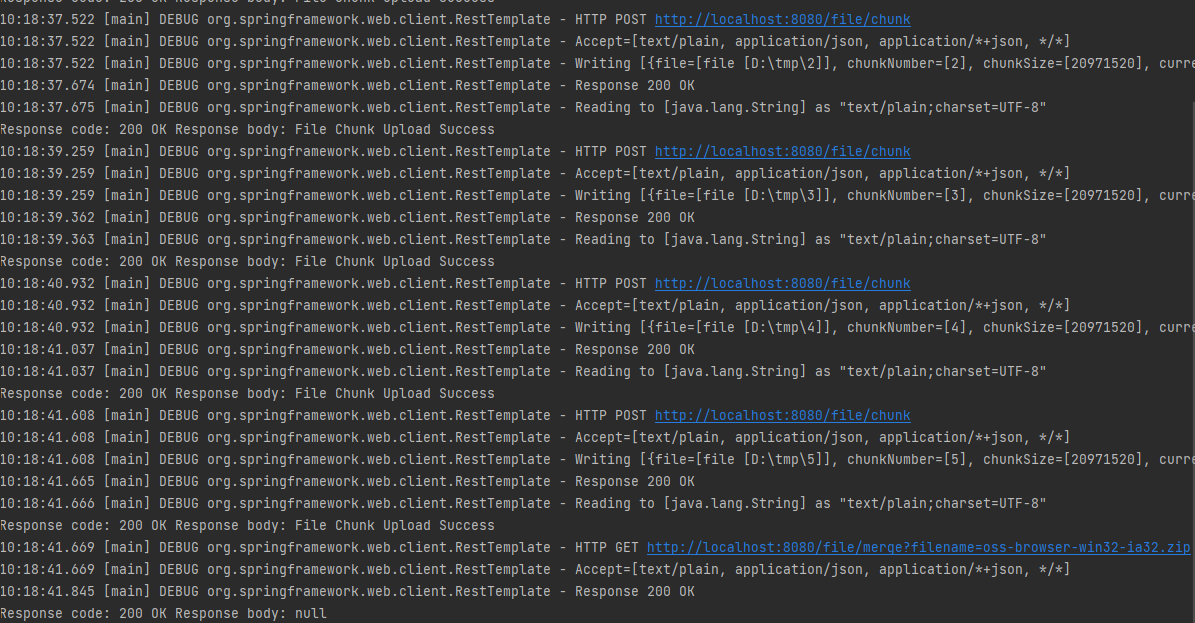
#include <cstdio>using namespace std;typedef unsigned long long ll;ll cal(ll n)
{ll j = 0,ans = 0;for(ll i = 1;i <= n;i = j + 1){j = n / (n / i);ans += (i + j) * (j - i + 1) * (n / i) / 2;}return ans;
}int main()
{ll a,b;scanf("%lld%lld",&a,&b);printf("%lld\n",cal(b) - cal(a - 1));return 0;
}