爬楼梯专题
代码随想录训练营day37|52. 携带研究材料,518.零钱兑换II,377. 组合总和 Ⅳ,70. 爬楼梯
52. 携带研究材料 这是一个完全背包问题,就是每个物品可以无限放。 在一维滚动数组的时候规定了遍历顺序是要从后往前的,就是因为不能多次放物体。 所以这里能多次放物体只需要把遍历顺序改改就好了 # include<iostream># include<vector>using namespace std;int main(){int n,m;cin>>n>>m;std::vector<i
代码随想录算法训练营Day37|完全背包问题、518.零钱兑换II、377. 组合总和 Ⅳ、70. 爬楼梯(进阶版)
完全背包问题 和01背包最大区别就是一个物品可以重复放多次,因此遍历空间时可以从前往后。 import java.util.*;public class Main{public static void main (String[] args) {Scanner sc = new Scanner(System.in);int m = sc.nextInt
每日一练5:最小花费爬楼梯(含链接)
1.链接 最小花费爬楼梯_牛客题霸_牛客网 2.题目 3.代码 class Solution {public:int minCostClimbingStairs(vector<int>& cost) {vector<int> dp(cost.size() + 1);dp[0] = 0;dp[1] = 0;for(int i = 2; i <= cost.size() ; i++){d
leetcode746:最小花费爬楼梯
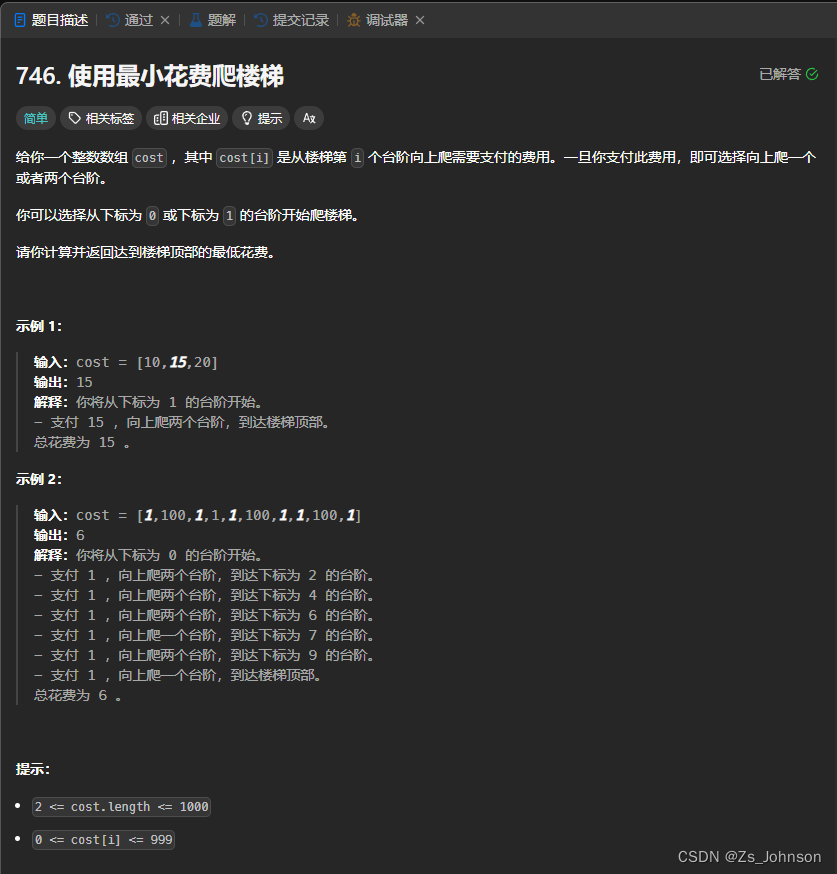
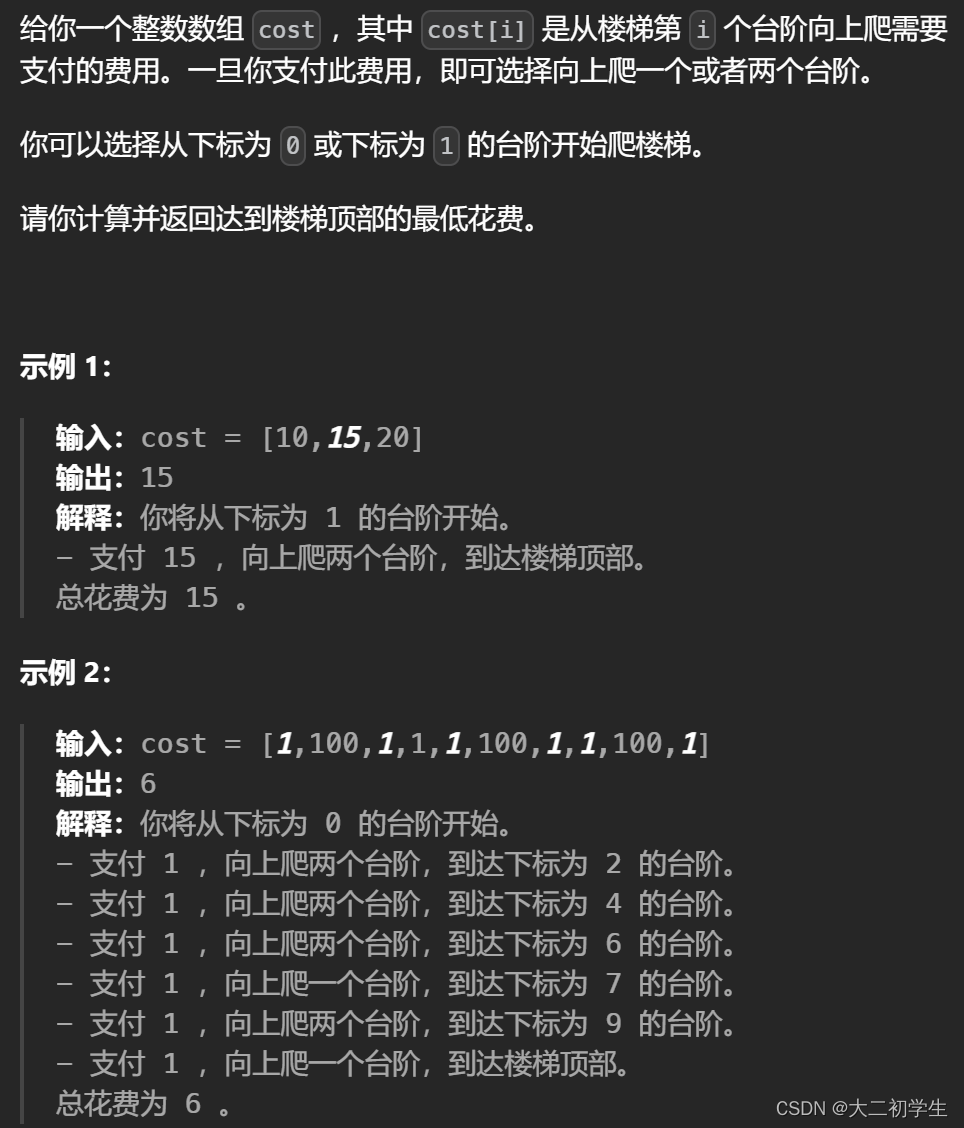
最小花费爬楼梯 给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。 你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。 请你计算并返回达到楼梯顶部的最低花费。 public int minCostClimbingStairs(int[] cost) {int[] dp = new int[
【hot100篇-python刷题记录】【爬楼梯】
R5-真正的动态规划 动态规划核心: 第i步是怎么来的(即动态规划公式) 走到第i步阶梯的总方法数=sum(走到第i-1步阶梯的总方法数,走到第i-2步阶梯的总方法数) class Solution:def climbStairs(self, n: int) -> int:if n<=2:return nsums=[0]*nsums[0],sums[1]=1,2for i in
动态规划DP--斐波那契数、爬楼梯、使用最小花费爬楼梯等示例代码
动态规划DP 文章目录 动态规划DP509. 斐波那契数70. 爬楼梯746. 使用最小花费爬楼梯62. 不同路径63. 不同路径II343.整数拆分 509. 斐波那契数 509. 斐波那契数 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) = 0,F(1) =
【代码随想录算法训练营第四十三天|卡码网52.携带研究材料、18.零钱兑换II、377.组合总和Ⅳ、卡码网57.爬楼梯】
文章目录 卡码网52.携带研究材料518.零钱兑换II377.组合总和Ⅳ卡码网57.爬楼梯 卡码网52.携带研究材料 这题是完全背包问题,完全背包问题在01背包问题的基础上其实主要是三个不同,第一个是初始化的时候不能再和01背包一样对第一个物品让背包大小大于物品重量的时候全部初始化为物品价值,因为现在的物品可以无限放。第二个就是动态规划内部的循环推导的时候不用倒序而是正序了,因为
代码随想录算法训练营第四十三天 | 完全背包理论基础、518.零钱兑换II、377. 组合总和 Ⅳ、70. 爬楼梯 (进阶)
完全背包理论基础 题目链接:https://kamacoder.com/problempage.php?pid=1052 文档讲解:https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9F… 视频讲解:https://www.bilibili.com/video/BV1uK41
算法训练 | 动态规划Part5 | 518.零钱兑换 II、377.组合总和 Ⅳ 、70.爬楼梯 (进阶)
目录 518. 零钱兑换 II 动态规划法 377. 组合总和 Ⅳ 动态规划法 70. 爬楼梯 (进阶) 动态规划法 518. 零钱兑换 II 题目链接:518. 零钱兑换 II - 力扣(LeetCode) 文章讲解:代码随想录 动态规划法 完全背包:01背包内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。而完全背包的物品是可以添加多次的,所以要从小
代码随想录算法训练营第43天(py)| 动态规划 | 完全背包、518. 零钱兑换 II、377. 组合总和 Ⅳ、爬楼梯
完全背包 完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。 有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。 01背包内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。 for(int i = 0; i < weight.siz
代码随想录算法训练营第四十三天| 377. 组合总和 Ⅳ、57. 爬楼梯(第八期模拟笔试)、322. 零钱兑换、279. 完全平方数
[LeetCode] 377. 组合总和 Ⅳ[LeetCode] 377. 组合总和 Ⅳ 文章解释 [LeetCode] 377. 组合总和 Ⅳ 视频解释 题目: 给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。 题目数据保证答案符合 32 位整数范围。 示例 1: 输入:nu
代码随想录算法训练营第38天|● 理论基础 ● 509. 斐波那契数● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
动态规划理论基础 动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。 所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的, 动态规划做题步骤 确定dp数组(dp table)以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组 动态规划
代码随想录算法训练营第三十八天| 509. 斐波那契数 ,70. 爬楼梯,746. 使用最小花费爬楼梯
509. 斐波那契数 - 力扣(LeetCode) class Solution {public int fib(int n) {if (n <= 1) {return n;}int[] dp = new int[n + 1];dp[0] = 0;dp[1] = 1;for (int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}re
【代码随想录算法训练Day38】LeetCode 509.斐波纳契数、LeetCode 76.爬楼梯、LeetCode 746. 使用最小花费爬楼梯
Day38 动态规划 又开始了新的章节,有了点难度的感觉。。 动态规划五部曲: 确定dp数组(dp table)以及下标的含义 确定递推公式 dp数组如何初始化 确定遍历顺序 举例推导dp数组 这些以后慢慢参透 LeetCode 509.斐波纳契数 最简单的动态规划,甚至不需要动态规划就可以解决的问题。初始状态、递推公式都已经有了,这道题就很简单了。 class Solution {pu
day 38 ||第九章 动态规划part01||509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯
509. 斐波那契数 首先我想的是递归方法,蒙对了,不过你自己对比一下你的递归和卡尔的递归,是不是还可以简化。。。。。 class Solution {public int fib(int n) {if(n==0) return 0;if(n == 1) return 1;int sum = recursion(n-1)+recursion(n-2);return sum;}private
【动态规划算法题记录】746. 使用最小花费爬楼梯
题目描述 给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。 你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。 请你计算并返回达到楼梯顶部的最低花费。 题目分析 这题答题思路我想的是对的,但是错在了推导上。 dp数组:dp[i]是到达第i层的最低消费 递推公式:我们当然知道爬到第
代码随想录算法训练营Day38|动态规划理论基础、2.斐波那契数、3.爬楼梯、4.使用最小花费爬楼梯
动态规划理论基础 代码随想录 (programmercarl.com) 动态规划(Dynamic Programming,简称DP)是一种算法设计技术,它通过将复杂问题分解为更小的子问题来解决优化问题。动态规划通常用于解决那些具有重叠子问题和最优子结构特性的问题。(可以理解为一种递推) 重叠子问题: 在递归算法中,相同的子问题会被多次计算。动态规划通过存储这些子问题的解来避
代码随想录算法训练营第38天 [ 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯]
代码随想录算法训练营第38天 [ 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯] 动态规划做题顺序 1.明确dp数组的含义 2.递推公式 3.dp数组的初始化 4.确认遍历的顺序 5.举例看看递推公式满不满足 一、509. 斐波那契数 链接: 代码随想录. 思路:经典dp数组 做题状态:看解析后做出来了 class Solution {public
【动态规划算法题记录】70. 爬楼梯——递归/动态规划
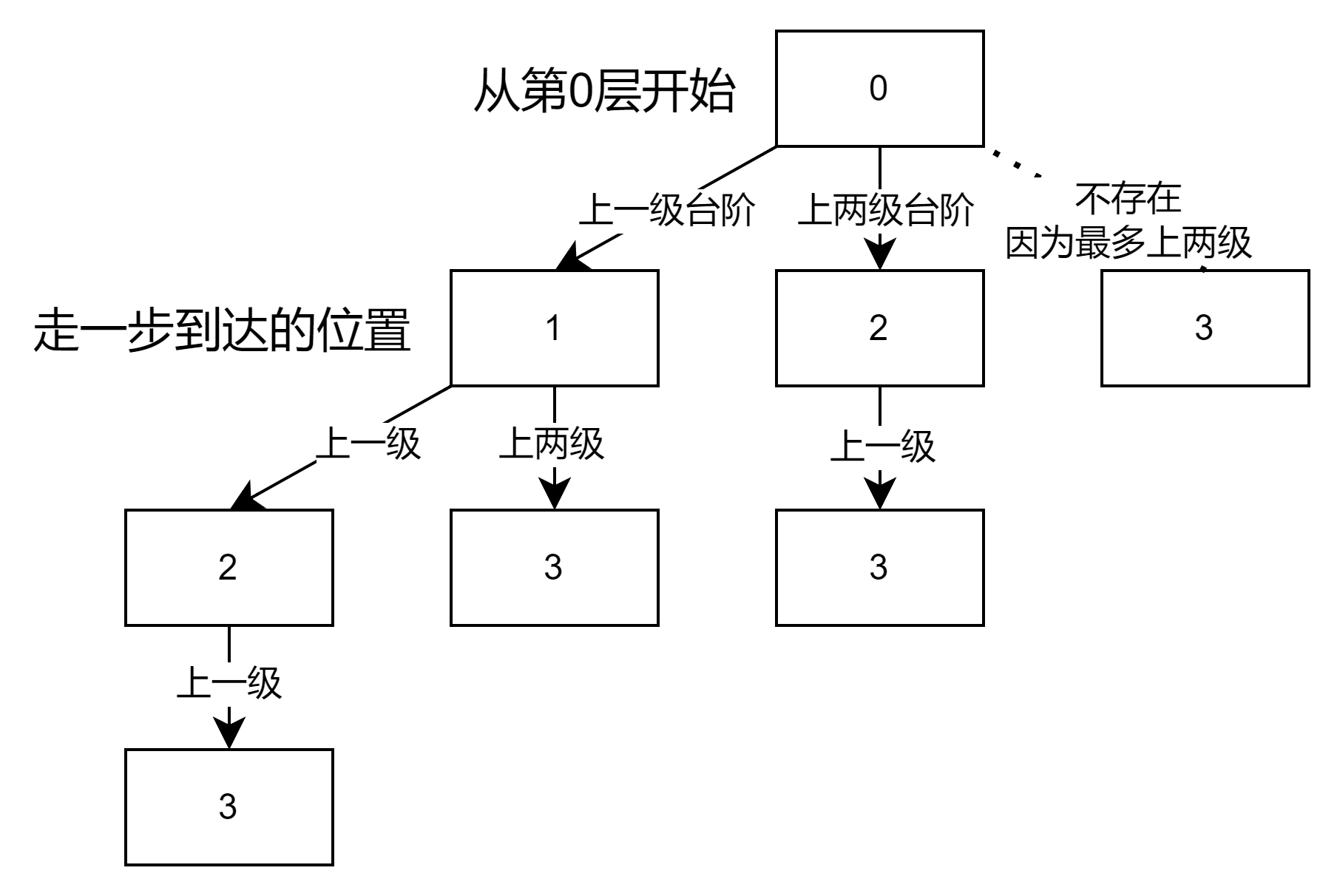
题目描述 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 题目分析 递归法(超出时间限制) 递归参数与返回值 void reversal(int i, int k) 每次我们处理第i个台阶到第k个台阶之间的可能性。这里我把结果int cnt放在类成员中了,所以直接在函数中进行处理,不用返回。递归终止条件 当我们处
2024/06/11--代码随想录算法1/17|理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
理论基础 动态规划:当前状态由前面的状态推导而来 贪心:局部选最优 动态规划5步曲 确定dp数组(dp table)以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组 509. 斐波那契数 力扣链接 动态规划5步曲 确定dp数组(dp table)以及下标的含义:dp[i]是F(i)确定递推公式,dp[i] = dp[i-1]+dp[i-2] i>1dp
刷代码随想录有感(99):动态规划——使用最小花费爬楼梯
题干: 代码: class Solution {public:int minCostClimbingStairs(vector<int>& cost) {vector<int>dp(cost.size() + 1);dp[0] = 0;dp[1] = 0;for(int i = 2; i <= cost.size(); i++){dp[i] = min(dp[i - 1] + cost[
力扣题解-746. 使用最小花费爬楼梯(动态规划)
题目:746. 使用最小花费爬楼梯 数组的每个索引作为一个阶梯,第 i个阶梯对应着一个非负数的体力花费值 costi。 每当你爬上一个阶梯你都要花费对应的体力花费值,然后你可以选择继续爬一个阶梯或者爬两个阶梯。 您需要找到达到楼层顶部的最低花费。在开始时,你可以选择从索引为 0 或 1 的元素作为初始阶梯。 示例 1: 输入: cost = [10, 15, 20] 输出: 15 解释:
刷代码随想录有感(98):动态规划——爬楼梯
题干: 代码: class Solution {public:int climbStairs(int n) {if(n == 1)return 1;if(n == 2)return 2;vector<int>dp(n + 1);dp[0] = 0;dp[1] = 1;dp[2] = 2;for(int i = 3; i <= n; i++){dp[i] = dp[i - 1] + dp[
day38 ● 理论基础 ● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
509. 斐波那契数 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) = 0,F(1) = 1F(n) = F(n - 1) + F(n - 2),其中 n > 1 给定 n ,请计算 F(n) 。 示例 1: 输入:n = 2输出:1解释:F(2) = F(1) +
算法:70. 爬楼梯
70. 爬楼梯 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 示例 1: 输入:n = 2输出:2解释:有两种方法可以爬到楼顶。1. 1 阶 + 1 阶2. 2 阶 示例 2: 输入:n = 3输出:3解释:有三种方法可以爬到楼顶。1. 1 阶 + 1 阶 + 1 阶2. 1 阶 + 2 阶



![爬楼梯[简单]](https://i-blog.csdnimg.cn/direct/5ab3dce210dd47669c14e174b7e8d4a6.png)