本文主要是介绍刷代码随想录有感(99):动态规划——使用最小花费爬楼梯,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题干:
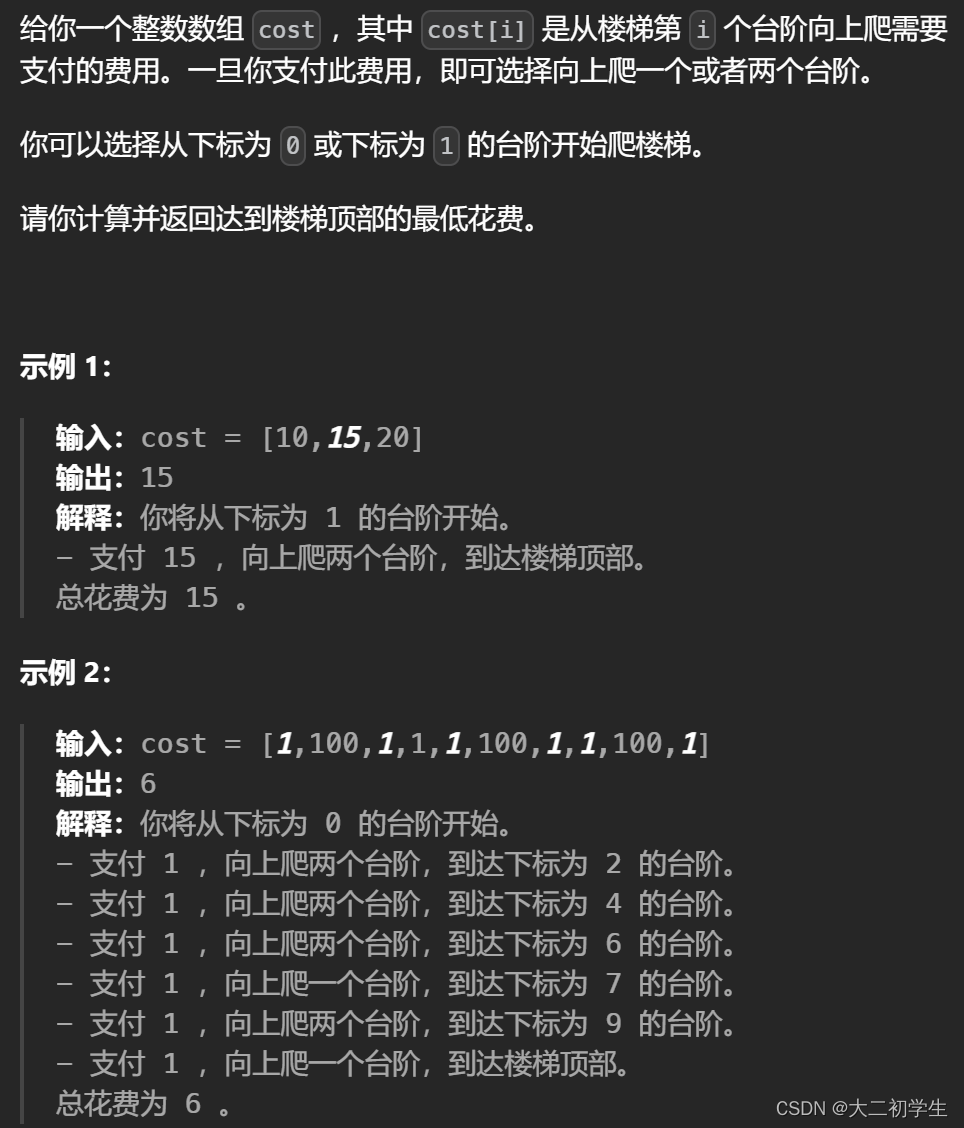
代码:
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {vector<int>dp(cost.size() + 1);dp[0] = 0;dp[1] = 0;for(int i = 2; i <= cost.size(); i++){dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}return dp[cost.size()];}
};dp[i]含义:到达这个台阶之前已经所花的最小花费。
递推公式:dp[i]是dp[i-1]+cost[i-1]与dp[i-2]+cost[i-2]中的较小值。
初始化:题干提到可以从下标0或1开始,所以‘站上去’不需要花费,dp[0]=dp[1]=0。
遍历顺序:从前向后遍历cost数组。
这篇关于刷代码随想录有感(99):动态规划——使用最小花费爬楼梯的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




