散度专题
KL散度(Kullback-Leibler divergence)
K L KL KL散度( K u l l b a c k − L e i b l e r d i v e r g e n c e Kullback-Leibler\ divergence Kullback−Leibler divergence),也被称为相对熵、互熵或鉴别信息,是用来衡量两个概率分布之间的差异性的度量方法。以下是对 K L KL KL散度的详细解释: 定义 K L KL
信息熵,交叉熵,相对熵,KL散度
熵,信息熵在机器学习和深度学习中是十分重要的。那么,信息熵到底是什么呢? 首先,信息熵是描述的一个事情的不确定性。比如:我说,太阳从东方升起。那么这个事件发生的概率几乎为1,那么这个事情的反应的信息量就会很小。如果我说,太阳从西方升起。那么这就反应的信息量就很大了,这有可能是因为地球的自转变成了自东向西,或者地球脱离轨道去到了别的地方,那么这就可能导致白天变成黑夜,热带雨林将
从概率角度出发,对交叉熵和 KL 散度进行分析和推导
🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 1. 定义与推导 交叉熵(Cross Entropy) 交叉熵是一个衡量两个概率分布之间差异的指标。在机器学习中,这通常用于衡量真实标签的分布与模型预测分布之间的差异。对于两个概率分布 P P P 和 Q Q Q,其中 P P P 是真实分布, Q Q Q 是模型预测分布,交叉熵的定义为:
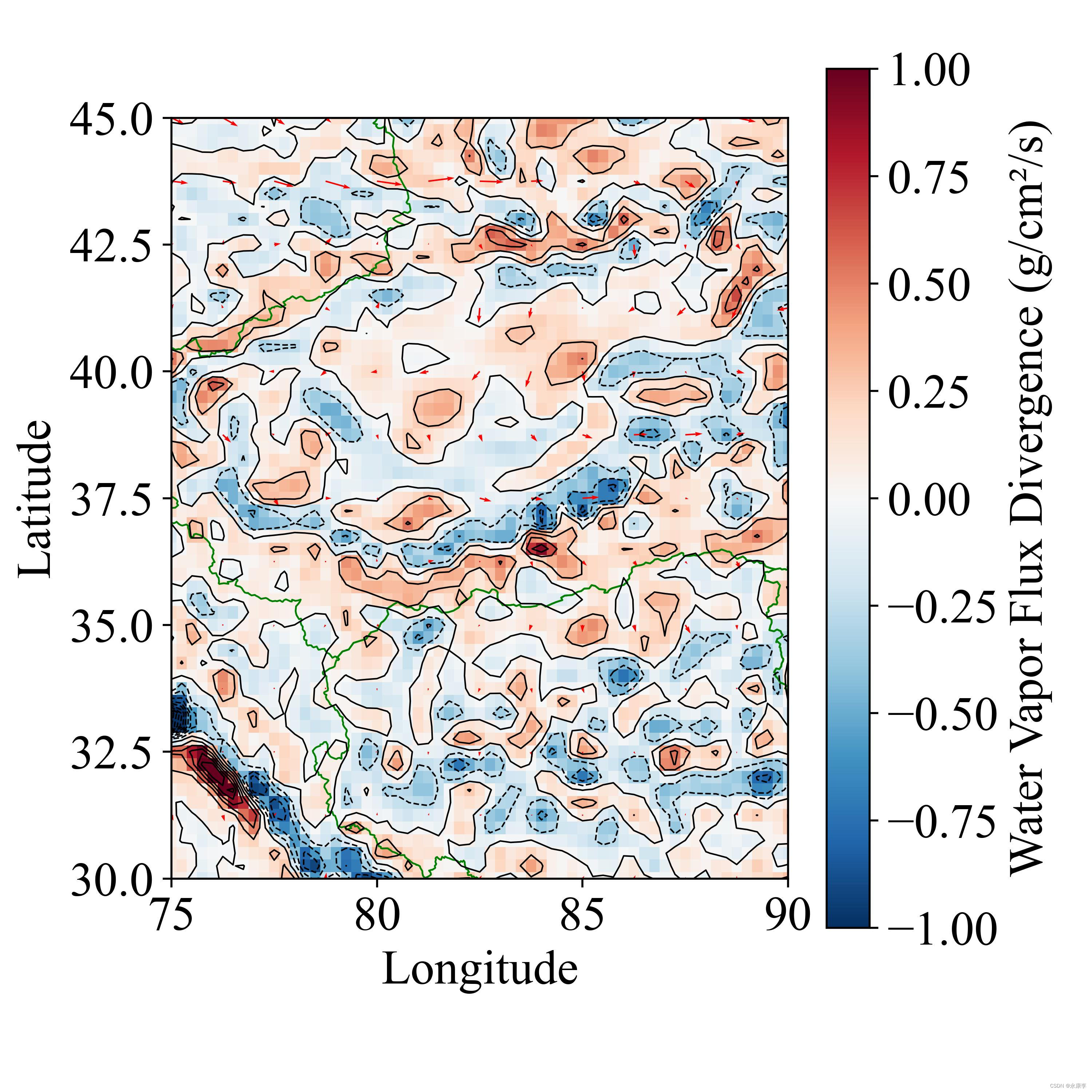
python ERA5 画水汽通量散度图地图:风速风向矢量图、叠加等高线、色彩分级、添加shp文件、添加位置点及备注
动机 有个同事吧,写论文,让我帮忙出个图,就写了个代码,然后我的博客好久没更新了,就顺便贴上来了! 很多人感兴趣风速的箭头怎样画,可能这种图使用 NCL 非常容易,很多没用过代码的小朋友,就有点犯怵,怕 python 画起来很困难。但是不然,看完我的代码,就会发现很简单,并且也可以批量,同时还能自定义国界等shp文件,这对于发sci等国际论文很重要,因为有时候内置的国界是有问题的。 数据 本
【域适应】基于散度成分分析(SCA)的四分类任务典型方法实现
关于 SCA(scatter component analysis)是基于一种简单的几何测量,即分散,它在再现内核希尔伯特空间上进行操作。 SCA找到一种在最大化类的可分离性、最小化域之间的不匹配和最大化数据的可分离性之间进行权衡的表示;每一个都通过分散进行量化。 参考论文:Shibboleth Authentication Request 工具 MATLAB 方法实现 SCA变换实
KL散度交叉熵信息熵不确定性信息度量
0.起源 物理学中的热力学 熵:度量分子在物理空间中的混乱程度; 1.信息熵 信息熵: 度量信息量的多少; 以离散信息为例 离散符号:x1,x2,…,xn; 信息中各符号出现的概率:p1,p2,…,pn; 信息的不确定性函数: f: p—f(p); p越大,信息的不确定性越小,因此f是一个 减函数; 假设前提: 各符号的出现是相互独立的(与实际不符) 则:f(p1,p2)=f(p1)+f(p
KL divergence(KL 散度)详解
本文用一种浅显易懂的方式说明KL散度。 参考资料 KL散度本质上是比较两个分布的相似程度。 现在给出2个简单的离散分布,称为分布1和分布2. 分布1有3个样本, 其中A的概率为50%, B的概率为40%,C的概率为10% 分布2也有3个样本: 其中A的概率为50%,B的概率为10%,C的概率为40%。 现在想比较分布1和分布2的相似程度。 直观看上去分布1和分布2中样本A的概率是一样的
熵、交叉熵和KL散度的基本概念和交叉熵损失函数的通俗介绍
交叉熵(也称为对数损失)是分类问题中最常用的损失函数之一。但是,由于当今庞大的库和框架的存在以及它们的易用性,我们中的大多数人常常在不了解熵的核心概念的情况下着手解决问题。所以,在这篇文章中,让我们看看熵背后的基本概念,把它与交叉熵和KL散度联系起来。我们还将查看一个使用损失函数作为交叉熵的分类问题的示例。 什么是熵? 为了开始了解熵到底指的是什么,让我们深入了解信息理论的一些基础知识。在这个
KL散度 pytorch实现
KL散度 KL Divergence D K L D_{KL} DKL 是衡量两个概率分布之间的差异程度。 考虑两个概率分布 P P P, Q Q Q(譬如前者为模型输出data对应的分布,后者为期望的分布),则KL散度的定义如下: D K L = ∑ x P ( x ) l o g P ( x ) Q ( x ) D_{KL} = \sum_xP(x)log\frac{P(x)}{Q
神经网络数学基础-香浓信息量、信息熵、交叉熵、相对熵(KL散度)
香浓信息量 这里以连续随机变量的情况为例。设 为随机变量X的概率分布,即 为随机变量 在 处的概率密度函数值,随机变量 在 处的香农信息量定义为: 这时香农信息量的单位为比特,香农信息量用于刻画消除随机变量在处的不确定性所需的信息量的大小。 如果非连续型随机变量,则为某一具体随机事件的概率。 为什么是这么一个表达式呢?想具体了解的可以参考如下的讨论: 知乎-香农的信息论究
交叉熵、KL散度、JS散度
信息量 符号 x x x的信息量定义为 x x x出现概率的倒数,单位比特 I ( x ) = log 1 P ( x ) I(x)=\log \frac{1}{P(x)} I(x)=logP(x)1 熵 平均信息量 H ( P ) = ∑ P ( x ) log 1 P ( x ) H(P)=\sum P(x)\log \frac{1}{P(x)} H(P)=∑P(x)log
Pinsker’s inequality 与 Kullback-Leibler (KL) divergence / KL散度
文章目录 Pinsker’s inequalityKullback-Leibler (KL) divergenceKL散度在matlab中的计算 KL散度在隐蔽通信概率推导中的应用 Pinsker’s inequality Pinsker’s Inequality是信息论中的一个不等式,通常用于量化两个概率分布之间的差异。这个不等式是由苏联数学家Mark Pinsker于1964
熵,KL散度(相对熵),交叉熵
信息量:-lg(p) I(), 一个事件发生的概率越大,则它发生时所携带的信息量就越小; 熵: -p*lg(p) 对一个事件,,...,所有可能的发生结果的信息量的期望E(I(X)),或者不确定性程度的期望; KL散度(相对熵): (注意前面没有负号) = = - H(p) 用来度量两个分布p(真实分布),q(假设分布)之间的差异(严格意义上不是距离,因为不满足交换
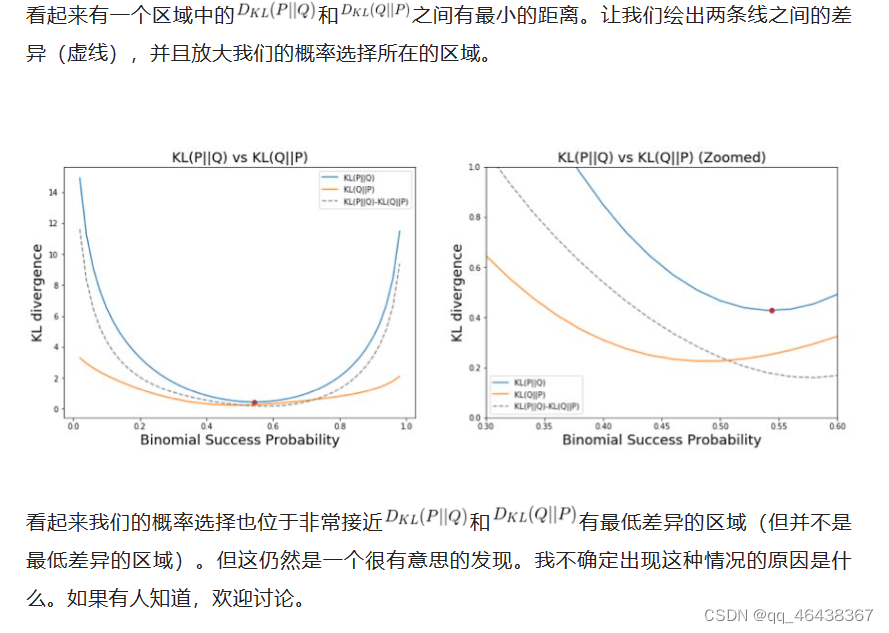
对KL散度的个人理解
此文参考这两篇文章: 一文直观理解KL散度 (qq.com) 进阶详解KL散度 - 知乎 (zhihu.com) 举例一个我们想要解决的问题: 上述博文中所解决的核心问题是这样的:假设我们是一组正在广袤无垠的太空中进行研究的科学家。我们发现了一些太空蠕虫,这些太空蠕虫的牙齿数量各不相同。现在我们需要将这些信息发回地球。但从太空向地球发送信息的成本很高,所以我们需要用尽量少的
Kullback-Leibler Divergence(KL散度)
下面一篇文章在例子中直观通俗理解KL散度: Kullback-Leibler Divergence Explained Light on Math Machine Learning: Intuitive Guide to Understanding KL 上文中文翻译链接:https://www.sohu.com/a/233776078_164987 知乎回答:https://www
KL散度 kl divergence
KL散度也叫KL距离 也叫相对熵 relative entropy。是描述两个概率分布P和Q差异的一种方法。它是非对称的,这意味着D(P||Q) ≠ D(Q||P)。特别的,在信息论中,D(P||Q)表示当用概率分布Q来拟合真实分布P时,产生的信息损耗,其中P表示真实分布,Q表示P的拟合分布。 离散随机变量的两个概率分布P、Q的KL散度定义为: 连续随机变量P,Q的KL散度定义为:
KL散度、CrossEntropy详解
文章目录 0. 概述1. 信息量1.1 定义1.2 性质1.3 例子 2. 熵 Entropy2.1 定义2.2 公式2.3 例子 3. 交叉熵 Cross Entropy3.1 定义3.2 公式3.3 例子 4. KL 散度(相对熵)4.1 公式
【扩散模型Diffusion Model系列】0-从VAE开始(隐变量模型、KL散度、最大化似然与AIGC的关系)
VAE VAE(Variational AutoEncoder),变分自编码器,是一种无监督学习算法,被用于压缩、特征提取和生成式任务。相比于GAN(Generative Adversarial Network),VAE在数学上有着更加良好的性质,有利于理论的分析和实现。 文章目录 VAE1 生成式模型的目标——KL散度和最大化似然MLE2 从AE到VAE3 VAE的损失函数4 结语
从香农熵到手推KL散度:一文带你纵览机器学习中的信息论
点击上方“中兴开发者社区”,关注我们 每天读一篇一线开发者原创好文 机器之心编译 参与:Nurhachu Null、蒋思源 信息论与信息熵是 AI 或机器学习中非常重要的概念,我们经常需要使用它的关键思想来描述概率分布或者量化概率分布之间的相似性。在本文中,我们从最基本的自信息和信息熵到交叉熵讨论了信息论的基础,再由最大似然估计推导出 KL 散度而加强我们对量
空间连通区域@曲面积分为零问题@通量和散度@高斯公式物理意义
文章目录 沿任意闭曲面的曲面积分为0的条件空间连通区域概念小结例 充要条件定理证明 通量和散度流量(通量)例 散度和高斯公式的物理意义借助速度场讨论一般向量场的散度小结例 高斯公式的向量场的通量和散度向量形式 沿任意闭曲面的曲面积分为0的条件 与讨论曲线积分中闭曲线积分为0的问题类似,这里讨论曲面积分 ∬ Σ P d y d z + Q d z d x + R d x d
机器学习中检验样本抽样的均匀——KL散度检验和K-S检验
最近做的一个项目中,需要对原来的数据进行一定量的采样形成训练集,因此需要保证采样的均匀性以保证样本参数的同分布性。 样本数据是这样的: ID.wavDate 可以看到,样本数据只有日期参数可以使用,所以我采用对抽样后的样本跟总体的日期参数进行分布检验的方法。 因为日期的分布不具有分布假设,所以需要用非参数检验方法,直接比较两个分布的差异,我找到两种方法: 1.机器学习中常用的K
有关熵、相对熵(KL散度)、交叉熵、JS散度、Wasserstein距离的内容
写在前面 最近学了一些关于熵的内容,为增强自己对这些内容的理解,方便自己以后能够温习,随手记录了相关的介绍,可能有不对的地方,敬请谅解。 信息量 任何事件都会承载一定的信息,事件发生的概率越大,其含有的信息量越少,事件发生的概率越小,其含有的信息量越多。比如昨天下雨了,是一个既定的事实,所以其信息量为0,天气预报说明天会下雨,是一个概率事件,其信息量相对较大。 假设 X X X是一个离散
KL散度(Kullback-Leibler_divergence)
KL-divergence,俗称KL距离,常用来衡量两个概率分布的距离。 1. 根据shannon的信息论,给定一个字符集的概率分布,我们可以设计一种编码,使得表示该字符集组成的字符串平均需要的比特数最少。假设这个字符集是X,对x∈X,其出现概率为P(x),那么其最优编码平均需要的比特数等于这个字符集的熵: a.当log以2为底的时候称之为 bits,结果可以视为多少个二进制位