KL散度交叉熵信息熵不确定性信息度量

本文主要是介绍KL散度交叉熵信息熵不确定性信息度量，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

0.起源

物理学中的热力学 熵：度量分子在物理空间中的混乱程度；

1.信息熵

信息熵： 度量信息量的多少；
以离散信息为例
离散符号：x₁，x₂，…，x_n；
信息中各符号出现的概率：p₁，p₂，…，p_n；
信息的不确定性函数： f： p—f（p）；
p越大，信息的不确定性越小，因此f是一个 减函数；
假设前提： 各符号的出现是相互独立的（与实际不符）
则：f（p₁，p₂）=f（p₁）+f（p₂），即f具有可加性；

满足 减函数和可加性 的不确定性函数f 定义为：

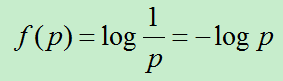
信息熵： 信息的平均不确定性

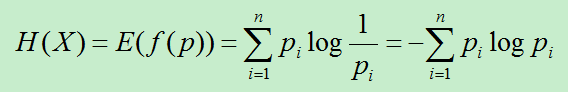
2.交叉熵

主要用于度量两个概率分布间的差异性信息。
P–X 真实分布 ； Q–Y拟合分布

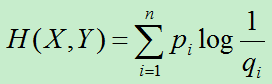
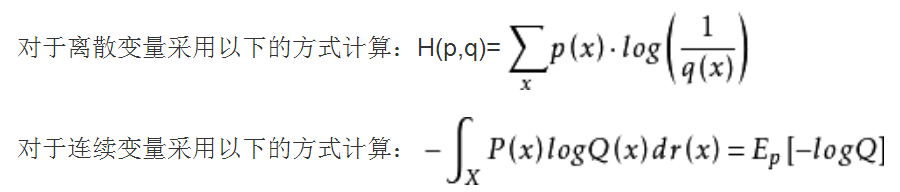
3.KL散度（相对熵）

相对熵（relative entropy），又被称为Kullback-Leibler散度（Kullback-Leibler divergence）或信息散度（information divergence），是两个概率分布（probability distribution）间差异的非对称性度量 。在信息论中，相对熵等价于两个概率分布的信息熵（Shannon entropy）的差值 。
相对熵是一些优化算法，例如最大期望算法（Expectation-Maximization algorithm, EM）的损失函数。此时参与计算的一个概率分布为真实分布，另一个为拟合分布，相对熵表示使用拟合分布拟合真实分布时产生的信息损耗。
P–X 真实分布 ； Q–Y拟合分布


特点： 非负性；分布 越相似，越接近0；

4.互信息

一个随机变量中包含的关于另一个随机变量的信息量，或者说是一个随机变量由于已知另一个随机变量而减少的不确定性。

**特点：**非负性；对称性；度量两个对象之间的相互性，对象 越相似，互信息越大；

这篇关于KL散度交叉熵信息熵不确定性信息度量的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---