本文主要是介绍信息熵,交叉熵,相对熵,KL散度,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
熵,信息熵在机器学习和深度学习中是十分重要的。那么,信息熵到底是什么呢?
首先,信息熵是描述的一个事情的不确定性。比如:我说,太阳从东方升起。那么这个事件发生的概率几乎为1,那么这个事情的反应的信息量就会很小。如果我说,太阳从西方升起。那么这就反应的信息量就很大了,这有可能是因为地球的自转变成了自东向西,或者地球脱离轨道去到了别的地方,那么这就可能导致白天变成黑夜,热带雨林将变成沙漠。
那么,太阳从东方升起这个事件,概率很大,信息量就会很少。相反,太阳从西方升起,概率很小,信息量就会很多。因此,信息熵常被用来作为一个系统的信息量的量化指标。信息熵也是不确定程度的度量, 一个事件的不确定程度越大, 则信息熵越大。
总结一下:消除熵=获取信息 (消除信息量)!
首先给出信息量的公式:
![]()
可以看到当p(x)取得最大值1时,h(x)=0,即对于一个确定事件,其信息量为0.
信息熵就是信息量的期望。公式如下:
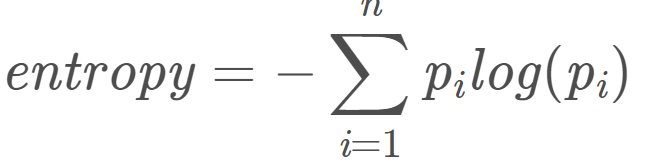
交叉熵:现在有样本集的两种概率分布p和q,其中p是样本的真实分布,q为预测分布(通过训练样本得到的分布),如果我们要用q来预测样本(对测试样本进行测试),则是基于分布q的信息量的期望,由于样本来自于分布p,因此期望与真实分布一致,所以基于q的样本预测公式为:

相对熵:用预测分布q预测样本 与 用真实分布p预测样本 的差值成为相对熵,又称为KL散度。

![]()
有两种方式可以证明KL(p|q)>=0:
第一种方式可以利用Jensen's Inequality来证明:
注: Jensen's Inequality 标准定义形式如下:如果X是一个随机变量且是一个凸函数,则:
由此可得:
![]()

第二种方式是直观解释:当编码对应的分布与样本对应的分布为同一分布时,即为最优编码状态,此时编码所需的全部比特数一定是最少的,其余任何方式都会使所需比特数增多,所以P与Q之间的KL散度不小于0。
KL散度除了基本的非负性,还有其它两个常见性质:
第一个是它的非对称性,即KL(p|q) 与KL(q|p)不相等。
第二个是KL散度并不满足三角不等式,即KL(p|q') + KL(q'|q) 与 KL(p|q) 没有明确的大小关系。
机器学习的目的是预测分布q更加接近于真实分布p,因此我们自然而然想到就是要求相对熵的最小值。而相对熵公式中的后一项由于p(x)的分布是确定的,因此可以说是常数,这样就变成了我们熟悉的,要求交叉熵的最小值,也即求最大似然估计。
这篇关于信息熵,交叉熵,相对熵,KL散度的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







