对KL散度的个人理解

此文参考这两篇文章：

一文直观理解KL散度 (qq.com)

进阶详解KL散度 - 知乎 (zhihu.com)

举例一个我们想要解决的问题：

上述博文中所解决的核心问题是这样的：假设我们是一组正在广袤无垠的太空中进行研究的科学家。我们发现了一些太空蠕虫，这些太空蠕虫的牙齿数量各不相同。现在我们需要将这些信息发回地球。但从太空向地球发送信息的成本很高，所以我们需要用尽量少的数据表达这些信息。我们有个好方法：我们不发送单个数值，而是绘制一张图表，其中 X 轴表示所观察到的不同牙齿数量（0,1,2…），Y 轴是看到的太空蠕虫具有 x 颗牙齿的概率（即具有 x 颗牙齿的蠕虫数量/蠕虫总数量）。这样，我们就将观察结果转换成了分布。

发送分布比发送每只蠕虫的信息更高效。但我们还能进一步压缩数据大小。我们可以用一个已知的分布来表示这个分布（比如均匀分布、二项分布、正态分布）。举个例子，假如我们用均匀分布来表示真实分布，我们只需要发送两段数据就能恢复真实数据；均匀概率和蠕虫数量。但我们怎样才能知道哪种分布能更好地解释真实分布呢？这就是 KL 散度的用武之地。

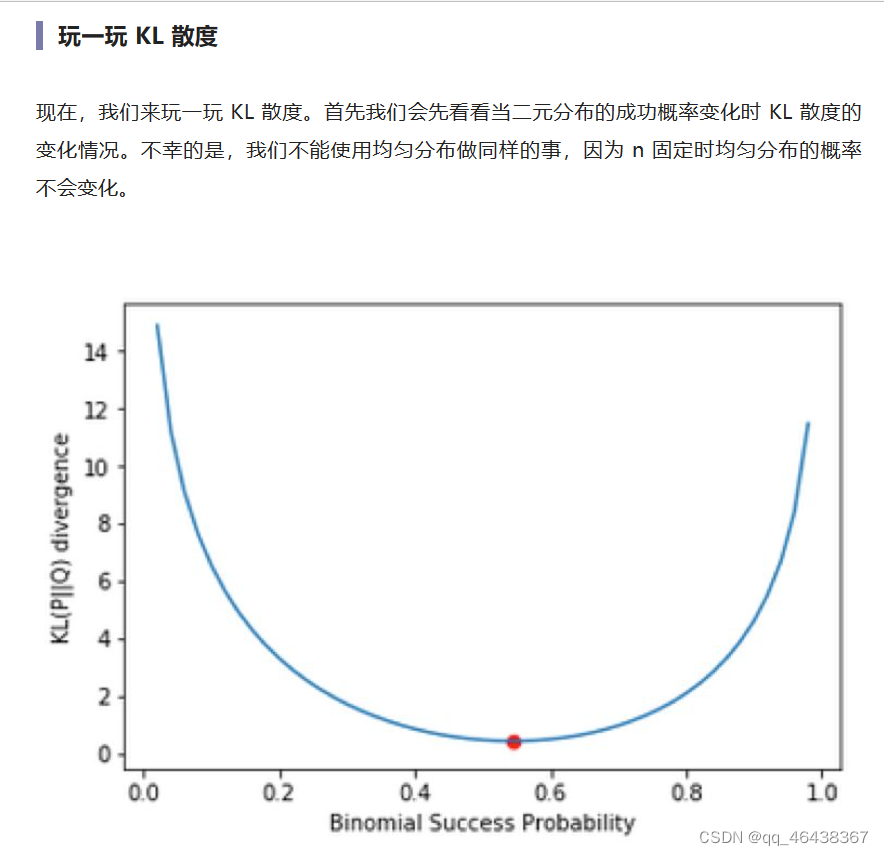
可以看到，当我们远离我们的选择（红点）时，KL 散度会快速增大。实际上，如果你显示输出我们的选择周围小 Δ 数量的 KL 散度值，你会看到我们选择的成功概率的 KL 散度最小。

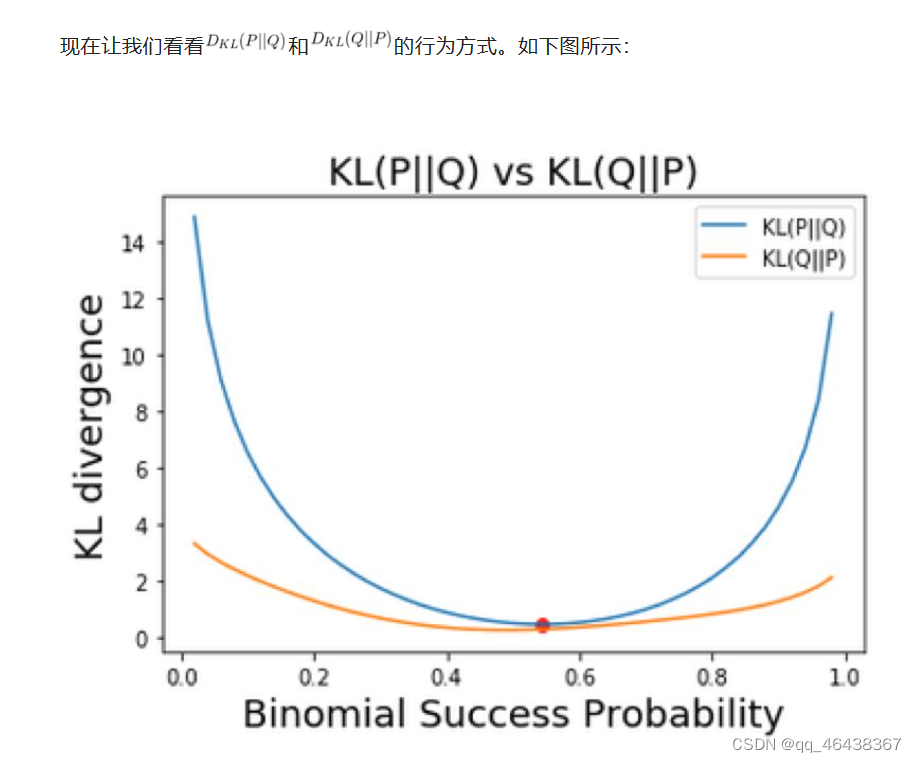
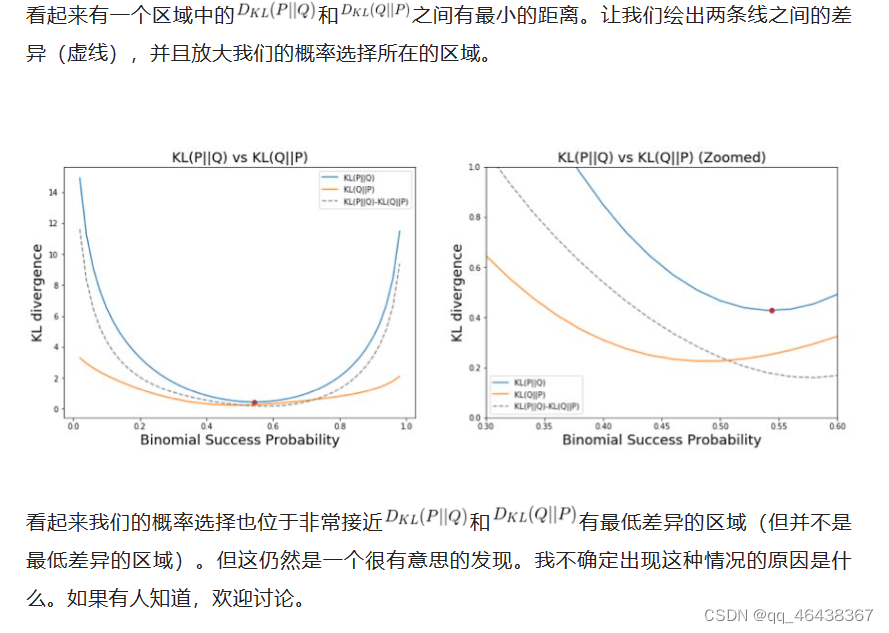
现在我们有些可靠的结果了。尽管均匀分布看起来很简单且信息不多而二项分布带有更有差别的信息，但实际上均匀分布与真实分布之间的匹配程度比二项分布的匹配程度更高。说老实话，这个结果实际上让我有点惊讶。因为我之前预计二项分布能更好地建模这个真实分布。因此，这个实验也能告诉我们：不要只相信自己的直觉！