熵、交叉熵和KL散度的基本概念和交叉熵损失函数的通俗介绍

交叉熵（也称为对数损失）是分类问题中最常用的损失函数之一。但是，由于当今庞大的库和框架的存在以及它们的易用性，我们中的大多数人常常在不了解熵的核心概念的情况下着手解决问题。所以，在这篇文章中，让我们看看熵背后的基本概念，把它与交叉熵和KL散度联系起来。我们还将查看一个使用损失函数作为交叉熵的分类问题的示例。

什么是熵？

为了开始了解熵到底指的是什么，让我们深入了解信息理论的一些基础知识。在这个数字时代，信息是由位（0和1）组成的。在通信时，有些位是有用的，有些是多余的，有些是错误的，等等。当我们传递信息时，我们希望尽可能多地向接收者传递有用的信息。

在Claude Shannon的论文“通信数学理论（1948）”中，他指出传输1位信息意味着将接收者的不确定性降低2倍。

让我们看看他是什么意思。例如，假设一个地方的天气是随机的，每天都有50-50个晴天或下雨的机会。

现在，如果一个气象站告诉你明天会下雨，那么他们已经把你的不确定性降低了2倍。起初，有两种可能性相同，但在收到气象站的最新消息后，我们只有一种可能性。在这里，气象台给我们发送了一点有用的信息，不管他们如何编码这些信息，这都是真的。

即使发送的消息是“未雨绸缪”的，每个字符占用一个字节，消息的总大小对应40位，但它们仍然只传递1位有用信息。

假设天气有8种可能的状态，所有的可能性都一样。

现在，当气象台给你第二天的天气时，他们会把你的不确定性降低8倍。由于每个事件都有1/8的机会发生，因此折减系数为8。

但如果可能性不一样呢？比如说，75%的几率是晴天，25%的几率是雨天。

现在，如果气象台说第二天会下雨，那么你的不确定性就降低了4倍，这是2位信息。不确定性的降低只是事件概率的倒数。在这种情况下，25%的反比是4，对数（4）到基2等于2。所以，我们得到了2位有用的信息。

如果气象台说第二天会是晴天，那么我们就能得到0.41位有用的信息。那么，我们平均要从气象站得到多少信息呢？

好吧，有75%的可能性明天会是晴天，这给了你0.41比特的信息，25%的可能性明天会下雨，这给了你2比特的信息，这相当于，

我们平均每天从气象站得到0.81位信息。所以，我们刚才计算的是熵。这是一个很好的衡量事件有多不确定的指标。它是由，

熵的方程现在完全有意义了。它测量你每天学习天气时得到的平均信息量。一般来说，它给出了我们从一个给定概率分布的样本中得到的平均信息量，它告诉我们概率分布是多么不可预测。

如果我们生活在一个每天都是晴天的沙漠中间，平均来说，我们每天从气象站得不到多少信息。熵将接近于零。另一方面，如果天气变化很大，熵就会大得多。

交叉熵

现在，我们来谈谈交叉熵。它只是平均消息长度。考虑到8种可能的天气条件的相同示例，所有这些条件都同样可能，每个条件都可以使用3位编码。

这里的平均消息长度是3，这就是交叉熵。但现在，假设你生活在一个阳光充足的地区，那里的天气概率分布如下：

每天有35%的可能性是晴天，只有1%的可能性是雷雨。所以，我们可以计算这个概率分布的熵，

Entropy = -(0.35 * log(0.35) + 0.35 * log(0.35) + 0.1 * log(0.1) + 0.1 * log(0.1) + 0.04 * log(0.04) + 0.04 * log(0.04) + 0.01 * log(0.01) + 0.01 * log(0.01))

Entropy = 2.23 bits

注意，这里使用的二元的记录。

所以，平均来说，气象台发送3位，但收信人只能得到2.23个有用的位。我们可以做得更好。

例如，让我们这样更改代码：

我们现在只使用2位表示晴天或部分晴天，3位表示多云和大部分多云，4位表示小雨和中雨，5位表示大雨和雷雨。天气的编码方式是明确的，如果你链接多条信息，只有一种方法可以解释比特序列。例如，01100只能表示部分晴天，然后是小雨。所以，如果我们计算电台每天发送的平均比特数，

35%*2 + 35%*2 + 10%*3 + 10%* 3+ 4%*4 + 4%*4 + 1%*5 + 1%*5 = 2.42 bits

这是我们的新的和改进的交叉熵，比之前的3位要好。现在，假设我们在不同的地方使用相同的代码，那里的天气正好相反，而且大部分时间都在下雨。

我们计算交叉熵，

1%*2 + 1%*2 + 4%*3 + 4%* 3+ 10%*4 + 10%*4 + 35%*5 + 35%*5 = 4.58 bits

我们得到4.58比特。大约是熵的两倍。平均而言，电台发送4.58位，但只有2.23位对接收者有用。它发送的信息是每条消息所需信息的两倍。这是因为我们使用的代码对天气分布做了一些隐含的假设。例如，当我们对晴天使用2位消息时，我们隐式地预测晴天的概率为25%。这是因为负二元对数（0.25）给出2。

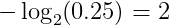
同样，我们计算所有的天气条件。

分母中2的幂对应于用于传输消息的位数。现在，很明显，预测的分布q与真实的分布p有很大的不同。

因此，现在我们可以将交叉熵表示为真概率分布p和预测概率分布q的函数，其表示为：

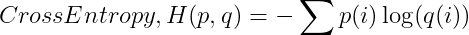
注意，我们示例中使用的是以2为基数的。

如你所见，它看起来与熵方程非常相似，除了我们在这里使用预测概率的对数。如果我们的预测是完美的，即预测分布等于真分布，那么交叉熵就是简单的熵。但是，如果分布不同，那么交叉熵将比熵大一些位。交叉熵超过熵的量称为相对熵，或者更常见的称为Kullback-Leibler散度（KL散度）。简而言之，

从上面的例子，我们得到K-L散度=交叉熵 - 熵=4.58–2.23=2.35位。

应用

现在，让我们在应用程序中使用交叉熵。考虑到我们正在训练一个图像分类器来对外观基本相似的不同动物进行分类，例如浣熊、小熊猫、狐狸等等。

因此，对于可能的7个类中的每一个，分类器估计一个概率，这称为预测分布。由于这是一个有监督的学习问题，我们知道真实的分布。

在上面的例子中，我拍摄了一只浣熊的图像，所以在真实分布中，它的概率是100%，其他的概率是0。我们可以用这两种分布之间的交叉熵作为代价函数，称之为交叉熵损失。

这只是我们前面看到的方程，除了它通常使用自然对数而不是二元对数。这对于训练来说并不重要，因为二元对数（x）等于自然对数（x）/log（2），其中分母是常数。

因此，当类概率被称为一个热向量时（这意味着一个类有100%，其余的都是0），那么交叉熵就是真类估计概率的负对数。

在这个例子中，交叉熵=1*log（0.3）=-log（0.3）=1.203

现在，当真类的预测概率接近0时，代价将变得非常大。但当预测概率接近1时，成本函数接近于0。

由于得到的损失较多（由于预测的分布太低），我们需要为每一类训练更多的例子来减少损失量。

结论

我们以气象站更新次日天气为例，了解香农信息论的概念。然后我们把它与熵和交叉熵联系起来。最后，我们以一个例子来说明交叉熵损失函数的实际应用。希望本文能澄清熵、交叉熵和KL散度背后的基本概念及其相互关系。

作者：Aakarsh Yelisetty

deephub翻译组