通俗专题

【生成模型系列（初级）】嵌入（Embedding）方程——自然语言处理的数学灵魂【通俗理解】

【通俗理解】嵌入（Embedding）方程——自然语言处理的数学灵魂关键词提炼 #嵌入方程 #自然语言处理 #词向量 #机器学习 #神经网络 #向量空间模型 #Siri #Google翻译 #AlexNet 第一节：嵌入方程的类比与核心概念【尽可能通俗】嵌入方程可以被看作是自然语言处理中的“翻译机”，它将文本中的单词或短语转换成计算机能够理解的数学形式，即向量。正如翻译机将一种语言

如何通俗理解注意力机制？

1、注意力机制（Attention Mechanism）是机器学习和深度学习中一种模拟人类注意力的方法，用于提高模型在处理大量信息时的效率和效果。通俗地理解，它就像是在一堆信息中找到最重要的部分，把注意力集中在这些关键点上，从而更好地完成任务。以下是几个简单的比喻来帮助理解注意力机制： 2、寻找重点：想象一下，你在阅读一篇文章的时候，有些段落特别重要，你会特别注意这些段落，反复阅读，而对其他部分

【C++学习（28）】通俗一点讲解：std::bind 回调技术

std::bind 是 C++11 标准库中的一个功能，它允许你“绑定”某些参数到一个函数、成员函数或可调用对象上，从而生成一个新的可调用对象。这种新的可调用对象可以稍后被调用，而且其中一些参数已经被预先设置好了。这在回调函数和异步编程中特别有用。下面我用一个通俗的例子来解释 std::bind 是如何工作的。假设场景假设你有一个家庭厨师，他有一个技能叫做“做饭”。做饭需要两个参数：一

Leetcode刷题笔记：多数元素(摩尔投票算法最通俗的理解)

关键点：给定的数组总是存在多数元素。出现次数大于 ⌊ n / 2 ⌋ \lfloor n/2\rfloor ⌊n/2⌋ 说明下面这种情况不会出现在测试用例中： [3,3,3,2,2,2,4] 或 [3,3,3,2,2,2] 也就是刚好有2个频率等于 ⌊ n / 2 ⌋ \lfloor n/2\rfloor ⌊n/2⌋ 的元素按照进阶要求，设计一个时间复杂度为 O(n)、空

【生成模型系列（中级）】词向量维度选择的奥秘——从理论到实验的揭秘【通俗理解，代码模拟】

【通俗理解】词向量维度选择的奥秘——从理论到实验的揭秘关键词提炼 #词向量 #维度选择 #最小熵原理 #Johnson-Lindenstrauss引理 #注意力机制 #图网络第一节：词向量维度选择的类比与核心概念【尽可能通俗】 1.1 词向量维度选择的类比词向量维度选择就像为一场复杂的烤肉方子挑选合适的食材和分量。每个词就像是烤肉中的不同食材，而维度就像是每种食材所需的分量。

Redisson的几种锁的通俗说明

Redisson的几种锁 Redisson 提供了多种分布式锁，每种锁都有其特定的使用场景，常见的包括： RLock（可重入锁）：允许同一线程多次获取锁。RReadWriteLock（读写锁）：多个线程可以同时读取数据，写操作是独占的。RSemaphore（信号量）：限制同一时刻能够访问共享资源的线程数量。RCountDownLatch（闭锁）：一个或多个线程等待其它线程完成任务。RFairL

【Get深一度】小波变换通俗解释 -算法与数学之美

链接：http://www.zhihu.com/question/22864189/answer/40772083 文章推荐人：杨晓东从傅里叶变换到小波变换，并不是一个完全抽象的东西，可以讲得很形象。小波变换有着明确的物理意义，如果我们从它的提出时所面对的问题看起，可以整理出非常清晰的思路。下面就按照傅里叶-->短时傅里叶变换-->小波变换的顺序，讲一下为什么会出现小波这个东

【Get深一度】小波分析概念3——正则性是什么意思，通俗解释

正则性英文是regularity，正则性一般用来刻画函数的光滑程度，正则性越高，函数的光滑性越好。通常用Lipschitz指数k来表征函数的正则性。度量函数的正则性时，消失矩的概念是重要的，若消失矩的阶数小于正则性指数，这是小波度量不出该

【Get深一度】小波分析概念2——消失矩阶数是什么意思，通俗解释

实际应用中，基本小波不仅要满足容许条件，还要施加所谓的消失矩（Vanishing Moments）条件原因：使尽量多的小波系数为零或者产生尽量少的非零小波系数目的：有利于数据压缩和消除噪声。小波的消失矩的定义：若

【Get深一度】小波分析概念1——紧支撑集是什么意思，通俗解释

最近学到小波，在仿真中也用到了紧支撑函数；紧支撑性越好，说明能量越集中；用最通俗的话来讲，紧支撑是这样的：对于函数f(x)，如果自变量x在 0附近的取值范围内，f(x)能取到 C；

面向对象23种设计模式通俗理解

终点即是起点,自强不息! 设计模式的理解设计模式是为了可重用代码、让代码更容易被他人理解、保证代码可靠性。模式：在某些场景下，针对某类问题的某种通用的解决方案。场景：项目所在的环境问题：约束条件，项目目标等解决方案：通用、可复用的设计，解决约束达到目标。设计模式的三个分类创建型模式：对象实例化的模式，创建型模式用于解耦对象的实例化过程。结构型模式：把类或对象结合在一

收藏：通俗讲解计算机工作原理

点击上方“朱小厮的博客”，选择“设为星标” 后台回复"书"，获取后台回复“k8s”，可领取k8s资料为解决各种问题，人们发明了不计其数的机器。计算机种类繁多，从嵌入火星漫游机器人的计算机到为操纵核潜艇导航系统的计算机，不一而足。冯• 诺伊曼在1945 年提出第一种计算模型，无论笔记本电脑还是电话，几乎所有计算机都遵循与这种模型相同的工作原理。那么你们了解计算机是如何工作的吗？本文将讨论这些内

卡尔曼滤波公式通俗理解

本文需要配合博客卡尔曼滤波详解进行理解 1.简单介绍参考卡尔曼滤波详解上面可简化理解为 2.主要过程主要过程还是参考卡尔曼滤波详解 3.实例这里以线性运动为例 3.1 前期定义状态和变量 3.1.1分析运动情况已知线性运动上一状态和当前状态的关系，假设没有噪声干扰，为 { x ′ = x + v x Δ t y ′ = y + v y Δ t \begin{

【通俗理解】深度学习特征提取——Attention机制的数学原理与应用

【通俗理解】深度学习特征提取——Attention机制的数学原理与应用关键词提炼 #深度学习 #特征提取 #Attention机制 #CNN #Transformer #关联特征 #MLP #拟合处理第一节：Attention机制的类比与核心概念 1.1 Attention机制的类比 Attention机制可以被视为一个“特征筛选器”，它像是一个精细的筛子，在众多的特征中筛选出

（每日一问）设计模式：如何通俗理解常见的设计模式？

（每日一问）设计模式：如何通俗理解常见的设计模式？本文旨在通过日常生活中的类比来通俗地解释常见的设计模式，帮助读者理解这些模式的核心思想。文章将设计模式分为创建型、结构型和行为型三大类，每种模式都通过生活中的具体事例进行类比解释，方便读者更直观地掌握这些概念。需要注意的是，本文不会涉及具体的代码实现，具体的实例代码将会在其他文章中详细介绍。文章目录（每日一问）设计模式：如

Kubernetes通俗讲解

目录什么是K8s？ K8s能做什么？ K8s的架构和组件 K8s的核心概念如何使用K8s？ K8s的优势 Kubernetes（简称K8s）是一个用于自动部署、扩展和管理容器化应用程序的开源平台。它以Google内部的Borg系统为蓝本开发，旨在简化大规模容器化应用的部署、管理和维护过程。下面我将用通俗易懂的语言来解释K8s的几个关键点：什么是K8s？ K8s是Ku

通俗范畴论11 对偶范畴与余积

对偶范畴与余积对偶的通俗意义对偶，我们并不陌生，例如唐朝杜甫的《绝句》：两个黄鹂鸣翠柳，一行白鹭上青天。窗含西岭千秋雪，门泊东吴万里船。 — 唐杜甫上面这首诗，是唐朝杜甫的《绝句》，我们可以发现，“两个”对应“一行”，“黄鹂”对应“白鹭”…，就说该诗中的上句，总是要求其下句的对应，这就是对偶。在范畴论中，对偶

傅立叶分析和小波分析之间的关系？（通俗讲解）

从傅里叶变换到小波变换，并不是一个完全抽象的东西，完全可以讲得很形象。小波变换有着明确的物理意义，如果我们从它的提出时所面对的问题看起，可以整理出非常清晰的思路。下面我就按照傅里叶-->短时傅里叶变换-->小波变换的顺序，讲一下为什么会出现小波这个东西、小波究竟是怎样的思路。（反正题主要求的是通俗形象，没说简短，希望不会太长不看。。）一、傅里叶变换关于傅里叶变换的基本概念在此我就不再赘

P(查准率) R(查全率) AP mAP最通俗准确的讲解

学习YOLO的过程中遇到了mAP指标，在网上看了很多关于mAP的讲解，不是很理解其计算过程，于是总结了各个帖子及自己的理解，给出mAP计算的规律，这样就能很好的记忆。目录一、P（精确率）、R（召回率）和F1 Score 二、PR曲线三、AP和mAP 一、P（精确率）、R（召回率）和F1 Score True Positive(TP): 预测对了。预测为正，实际为正。 Fals

机器学习/数据分析--通俗语言带你入门K-邻近算法(结合案例)

🍨 本文为🔗365天深度学习训练营中的学习记录博客🍖 原作者：K同学啊前言机器学习是深度学习和数据分析的基础，接下来将更新常见的机器学习算法注意：在打数学建模比赛中，机器学习用的也很多，可以一起学习欢迎收藏 + 点赞 + 关注文章目录 K-邻近算法模型简介1、模型简介2、模型难点与求解KNN难点解决方法K值选取问题选取K值后，如何遍历速度最快距离选取欧式距离曼

通俗范畴论4 范畴的定义

注：由于CSDN无法显示本文章源文件的公式，因此部分下标、字母花体、箭头表示可能会不正常，请读者谅解范畴的正式定义上一节我们在没有引入范畴这个数学概念的情况下，直接体验了一个“苹果1”范畴，建立了一个对范畴的直观。本节我们正式学习范畴的定义和基本性质。一个范畴(Category) C𝐶，由以下部分组成：数据：对象（Objects）：包含若干个对象（Objects），这些

用通俗到业余水平的语言教你编译和打包

本文从零开始讲述编译的基本过程，希望菜鸟们能喜欢。毕竟Linux下的软件，源代码是多于二进制包的，学会了编译，再安装软件就不求别人了。所以，编译也是Linux菜鸟必修的一课。 1，安装编译工具。 $ sudo apt-get install dpkg-dev file gcc g++ libc6-dev make patch perl autoconf automake dh-ma

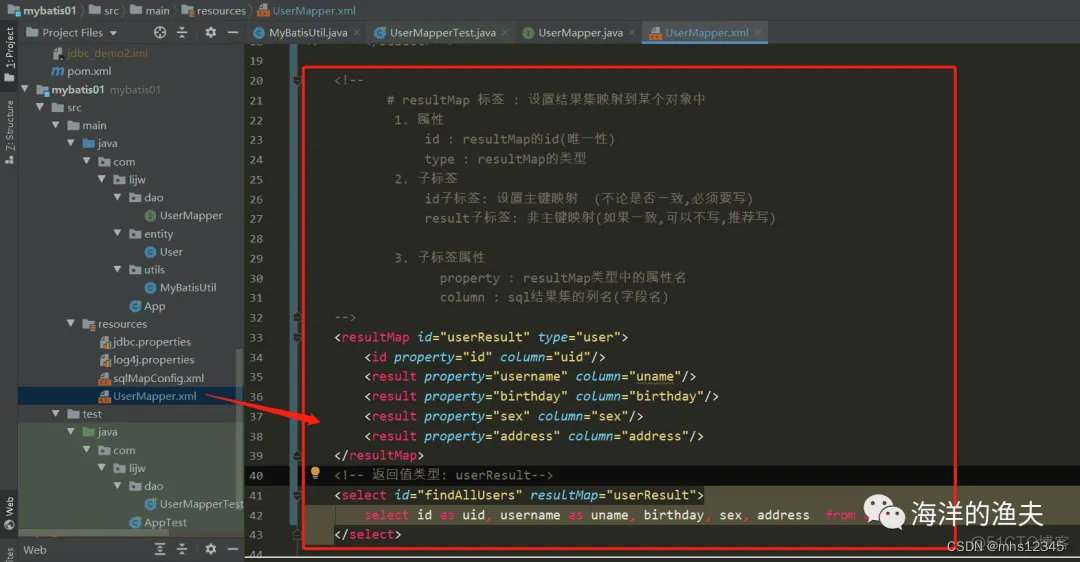
通俗解释resultType和resultMap的区别

【 1 对于单表而言：注：以下都是摘抄过来的，做了让自己更能理解的版本如果数据库返回结果的列名和要封装的实体的属性名完全一致的话用 resultType 属性如果数据库返回结果的列名（起了别名）和要封装的实体的属性名有不一致的情况用 resultMap 属性查询接口方法不需要改变，还是照样接收 List 作为查询的结果。【 2 对于多表而言：对于多表操作，无论是一

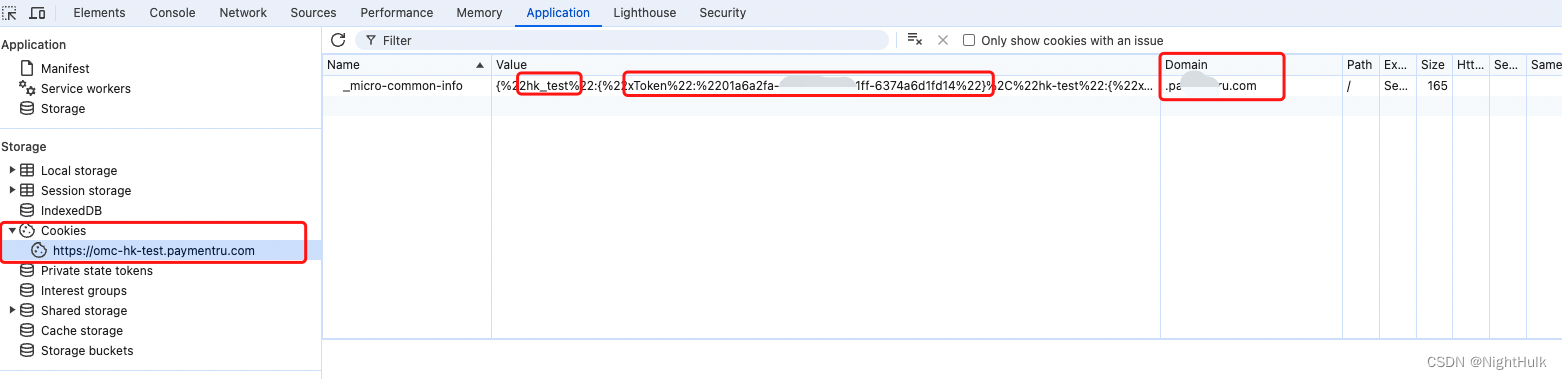
多网页登录Cookie免登通俗理解

背景，现在有A、B两个系统，其中B是乾坤框架的微前端，里面又有若干可以单独运行的系统C、D、E、F，现在的目标是，如果没有登录过其中任一系统，则需要跳转登录页登录，登录后，所有的A-F都不再需要登录，登录token有效期12h，每次访问都重新刷新12h，上面A-F的域名结尾都是abc.com如a.abc.com、b.abc.com 解决思路：利用浏览器的Cookie实现登录页面登录后，登录前

如何通俗理解逻辑回归(Logistic Regression)

首先, 什么是逻辑回归呢? 我们先来看一下逻辑回归的公式: t = w T X + b y = s i g m o i d ( t ) s i g m o i d ( t ) = 1 1 + e − t t = w^TX+b\\ y = sigmoid(t)\\ sigmoid(t) = \frac1{1+e^{-t}} t=wTX+by=sigmoid(t)sigmoid(t)=1+e−t1

数据和埋点的通俗解释

举一个生活的例子，让大家理解一下数据和埋点从前，小镇里新开了一家游乐园，游乐园里有各种各样的游乐设施，过山车、激流勇进、大摆锤、主题餐厅。大家非常喜欢，刚开业不久就收获了很多游客的青睐。运营了一段时间之后，游乐园为了让游客的游玩体验更好，决定对游乐园进行翻新装修。问题来了：过山车的工作人员说：“过山车需要翻新，大家都更喜欢过山车。”但大摆锤的工作人员却不同意：“大摆锤需要翻新，大