通俗范畴论4 范畴的定义

本文主要是介绍通俗范畴论4 范畴的定义，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

注：由于CSDN无法显示本文章源文件的公式，因此部分下标、字母花体、箭头表示可能会不正常，请读者谅解

范畴的正式定义

上一节我们在没有引入范畴这个数学概念的情况下，直接体验了一个“苹果1”范畴，建立了一个对范畴的直观。本节我们正式学习范畴的定义和基本性质。

一个范畴(Category) C𝐶，由以下部分组成：

• 数据：

  • 对象（Objects）：包含若干个对象（Objects），这些对象的全体构成一个聚集（Collection），这个聚集记为 ob(C)𝑜𝑏(𝐶)

  • 态射（morphisms）：对于对象 A,B∈ob(C)𝐴,𝐵∈𝑜𝑏(𝐶)，有一个态射构成的聚集 C(A,B)𝐶(𝐴,𝐵) 包含了 从 A𝐴 到 B𝐵 的所有态射 a→b𝑎→𝑏

• 结构：

  • 恒等态射（identities）：对于任何对象 A∈ob(C)𝐴∈𝑜𝑏(𝐶)，都有一个恒等态射 A−→−IdAA𝐴→𝐼𝑑𝐴𝐴

  • 复合（composition）：对于任何箭头 A→fB→gC𝐴→𝑓𝐵→𝑔𝐶，总有一个复合箭头 A−→−g∘fC𝐴→𝑔∘𝑓𝐶

• 性质：

  • 单位律（Unit Laws）：对于任何态射 A→fB𝐴→𝑓𝐵，总有：f∘IdA=f=IdB∘f𝑓∘𝐼𝑑𝐴=𝑓=𝐼𝑑𝐵∘𝑓

  • 结合律（Associativity）：对于任何态射 A→fB→gC→hD𝐴→𝑓𝐵→𝑔𝐶→ℎ𝐷，总有 (h∘g)∘f=h∘(g∘f)(ℎ∘𝑔)∘𝑓=ℎ∘(𝑔∘𝑓)

范畴定义涉及的名字

在不同的书中，范畴定义的形式可能会有所不同，但含义总是一样的。我们先来看名字。

在定义中，给某个范畴取了一个名字 C𝐶，这个符号是花写的大写C，这可能让您不太习惯，但是这样写，从视觉上就和普通的大写区分开来了。在定义里我们看到，对象也是用大写字母，A、B等，因为显示不同，您可以很容易区分，花写的是范畴，非花写的是一个范畴里面的对象。所以，如果你要用大写的C表示一个对象，那么，范畴的名称你可以用一个别的花写大写字母，例如：F𝐹。

然后，我们看态射，态射就是前述的箭头，它的符号表示一般用小写字母，f、g、h 等，这样就不容易和对象混起来，因为对象是大写字母。

对于恒等态射，因为每个对象都有一个唯一的恒等态射，因此我们要标记是哪个对象的恒等态射，因此名字有个下标，例如对于对象 X，则表示为 IdX。

然后是箭头的复合，即连续的箭头，可以组成一个更长的箭头，复合这个操作，我们用 ∘∘ 表示，例如 g∘f𝑔∘𝑓，有时写起来比较麻烦，我们会直接写为 gf。

注意这些名字的取法，对于范畴定义本身是无关紧要的，因此不同书中名字可能不同，显示形式也可能有所差别，但是C无论花不花写，C就是C。当然，一个好的显示形式，可以在阅读的时候方便区分，例如：

A∈D𝐴∈𝐷 就容易混，而 A∈D𝐴∈𝐷，就不容易混，A是对象，D是范畴。

当然如果觉得花写麻烦，只用普通写法也行，在阅读或书写时，自己注意区分不同字母指代的含义就行。

范畴的表示

我们来看一个具体例子，一个范畴 C𝐶，有三个对象：A、B、C，A 态射 B，B 态射 C，C 态射 A。那么我们可以得到范畴的代数表示和有向图表示。

范畴的代数表示

C𝐶 由如下部分构成：

• 对象：ob(C)𝑜𝑏(𝐶) = {A, B, C}

• 恒等态射：C(A,A)𝐶(𝐴,𝐴)= {IdA}、C(B,B)𝐶(𝐵,𝐵)= {IdB}、C(C,C)𝐶(𝐶,𝐶)= {IdC}

• 对象间态射：

  C(A,B)𝐶(𝐴,𝐵)= {f}

  C(B,C)𝐶(𝐵,𝐶)= {g}

  C(C,A)𝐶(𝐶,𝐴)= {h}

  C(A,C)𝐶(𝐴,𝐶)= {g∘f}

  C(B,A)𝐶(𝐵,𝐴)= {h∘g}

  C(C,B)𝐶(𝐶,𝐵)= {f∘h}

范畴的有向图表示

C𝐶 用有向图来进行表示：

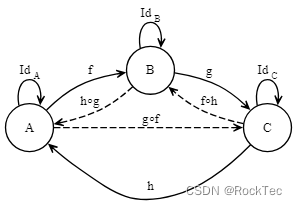
聚集（Collection）

在上述定义中，ob(C)𝑜𝑏(𝐶) 指一个范畴里面的所有对象构成的一个东西，C(A,B)𝐶(𝐴,𝐵) 指从对象A到对象B的所有态射构成的一个东西，也就是所有箭头构成的一个东西。我们只是给它们取了一个名字而已。

但是您可能会问，如果把对象和态射看成集合的元素，那 ob(C)𝑜𝑏(𝐶) 不就是由所有对象构成的一个集合，而 C(A,B)𝐶(𝐴,𝐵) 不就是由对象A到对象B的所有态射构成的集合么？为什么要用聚集（Collection）这个名字？

因为如果有一个范畴，它的对象是所有的集合，那么，这个包含所有集合的东西，不能是一个集合，这就是著名的罗素悖论。

我们做下思想实验，朴素集合论规定一个集合不能包含自己。但在这个实验中，我们考虑两种情况，集合可以包含自己以及集合不能包含自己。

首先考虑一个集合可以包含自己，把所有集合放到一起，构成一个集合A，因为A是刚刚才构建好的，它还没在A里面，根据A的定义，我们的集合A应该包含所有的集合，因此我们还得把A也放到集合A里面，这样就得到了集合B，嗯，这下应该OK了，但是，我们刚得到的这个集合B没在集合B里面，所以我们还得把集合B，放到集合B里面，这样就陷入了循环。

也许你会想，那定义集合为不能包含自己，不就行了？那么我们考虑所有不包含自己的集合所构成的集合A。集合A如果不包含自己，那么按照定义，它就得包含自己，如果它包含自己，那么它就违背了集合的定义，即，集合不能包含自己。

范畴论中的一个范畴，它包含的所有对象所构成的聚集ob(C)𝑜𝑏(𝐶)可以很“大”，比如包含所有的集合，每个集合是一个对象，而因为这所有对象构成的东西叫做聚集（Collection），聚集不算所有集合中的一个，这样就避免了罗素悖论。

在范畴论的定义中，使用聚集这个概念，准确描述了“把所有对象放到一起”，或“把所有从A到B的箭头放到一起”这个意思，范畴论的定义仅需要这个。这个聚集，比集合的要求少，它不必满足集合论的公理，同时，也不必具有集合论的所有运算，例如：交集、并集，甚至幂集等。这样，从定义的角度看，依赖最少，就说范畴的定义，不依赖于集合的定义，只依赖于一个大家都公认的概念，即我们可以把若干个东西放到一起，这个东西可以取个名字，叫做——聚集。

态射及其性质

态射含义初探

什么是态射？这是每一个学习范畴论学习者都会问的问题。好在我们之前学习了一些具体例子，所以，简单说，态射就是箭头，而箭头表示一种对应（Mapping），因此，态射就是一种对应，即将一个东西对应到一个东西。在范畴论里就是将一个对象对应到一个对象。态射与箭头在范畴论里是同义词，表示一个意思，即对应。

无损对应

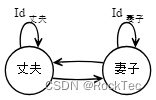
Figure 1. 丈夫妻子范畴

如上图所示，其中一个态射表示丈夫对应妻子，另一个态射表示妻子对应丈夫，显然这种对应只是表明了丈夫和妻子的关系，不会影响丈夫或妻子。

有损对应

有损对应也是一种对应，但是是一种特殊的对应，如下图所示：

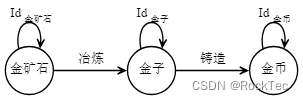
Figure 2. 金矿石范畴

我们让上图的金矿石对象，携带一块真的金矿石A，然后沿着箭头向右走，最后，我们发现，金矿石A变成了一个金币，取个名字叫做金币A，具体说就是：金矿石A首先变成了金子A，然后变成了金币A。这看起来不是对应啊。

但是写为如下形式，就了然了：

原来的金矿石A对应冶炼后得到的金子A，冶炼后的金子A对应将其铸造后的金币A。因此，这仍然是一种对应，只是在对应的过程中，对象携带的信息发生了变化：

• 一开始金矿石对象携带着金矿石A

• 经过冶炼，金矿石对象不再携带金矿石A，但金子对象携带着金子A

• 经过铸造，金币对象携带者金币A，而金子对象不再携带着金子A

我们再看一个例子，这个例子我们让范畴携带一个数学对象：

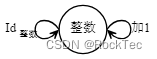
Figure 3. 整数加1范畴

假设上述范畴携带一个具体数字的信息，比如10，那么每次走“加1”这个箭头，这个具体数字都会加1。

从直观上讲，上述两例，是一个东西变成了一个东西，即变换（transform），变换是对应的一种特殊形式，因为变换改变了对象携带的信息，因此我们称为有损对应。无损对应和有损对应只是两个名字，方便我们更全面地理解对应的含义。

在其他书中，也许会这么说：态射的含义一般是映射和变换，那么即是指无损对应和有损对应。

需要特别注意的是，范畴对象，例如上面例子的金矿石和整数，它们指代的是金矿石和整数这两个概念，无论携带不携带具体信息，例如携带金矿石A或整数10，金矿石和整数这两个对象，作为范畴里面的实体，始终存在，不依赖于任何具体的金矿石或具体的整数。

态射的性质

一个范畴所包含的态射往往是非常丰富的，就说会有很多很多箭头，我们往往只画出我们关心的那些箭头，其他没有画出的默认存在。因此，为了之后的示意图简洁，我们约定，恒等箭头默认存在但是可以不画出，对于画出的箭头，可以给定具体名字，也可以不给定。对于示意图无关紧要的箭头，可以不画出。

复合

复合就是首尾相连的两个态射，或一个态射，可以构成一个新的态射。为叙述方便，因为态射和箭头在范畴论中是同义词，因此我们将混用这两种说法。

首先，需要说明的是，箭头的复合是范畴的一种要求，并不是箭头的自然性质。如下图所示：

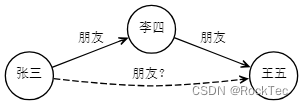
Figure 4. 非态射箭头

如上图所示，张三是李四的朋友，李四是王五的朋友，并不能推出张三是王五的朋友。因此我们不能画出张三到王五的箭头，从而上图不是一个范畴。

在范畴论中，我们要求，首尾相连的箭头，必须能够复合，凡是范畴论的态射，都必须可复合。如下图所示：

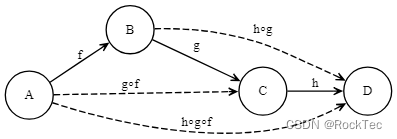
Figure 5. 态射的复合

如上图所示，A、B、C、D 分别由箭头f、g、h连接，于是我们立即得到：g∘f、h∘g和h∘g∘f三个箭头，在图中用虚线标出。g∘f念作 g复合f。

你可以把复合看作是态射的一种运算，凡首尾相接的任何两个箭头g和h，总可以进行h∘g的运算。这里注意一下写法：

参照上图，按照图中的箭头方向，是f然后g，但是f和g的复合，写为g∘f，表示先走f，然后接着走g，为什么要倒着写呢？如果我们写为嵌套形式就清楚了：g(f)，小括号先运算所以先走f，然后再走g，这个顺序恰好与g∘f的字母顺序一致。因此，你也可以把g∘f念作 g括f 或 g圈f，这样先后顺序就不会搞混。

有趣的是，如果箭头g自身首尾相接，则可以自身复合，得到新箭头g∘g，这个箭头还可以再次复合g，变成g∘g∘g，如此不断复合，可以得到无限多的箭头！

最后，你可能会问，为什么要规定箭头为可复合呢？这是因为范畴论非常关注可组合性，即通过箭头的复合，我们可以进行各种各样的对应或变换，从而建立一个强大的系统。如果箭头不能复合，或者不总是能复合，则这个系统的可组合性就会大打折扣，不是那么好操作了。因此范畴规定，箭头必须可复合，即箭头必须是个足够“友好”的箭头。

结合律

如果把箭头的复合看成运算，那么它是否满足：交换律、结合律、分配律呢？

首先，态射复合不满足交换律，g∘f ≠ f∘g，如下图所示：

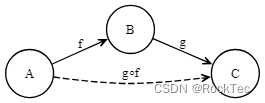
Figure 6. 态射的复合

观察上图，你会发现，f∘g，就是先从B走到C，再A走到B，完全连不起来，因此态射的复合必须保序，所以不满足交换律。

分配律指的是，对于两种运算，例如 "⋅" 和 "+" （注意这里点和加指两种特定的运算，不是数字的加和乘），若满足：a⋅(b+c)=(a⋅b)(a⋅c) 和 (a+b)⋅c=(a⋅c)(b⋅c)，则 "⋅" 对 "+" 满足分配律。因为我们的态射只有一个运算，那就是复合运算，所以无须考虑。

最后我们看结合律，范畴论要求，态射必须满足结合律，如下图所示：

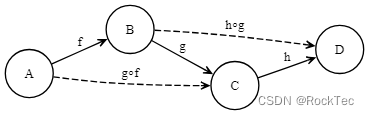
Figure 7. 态射的结合律

范畴论要求：(h∘g)∘f=h∘(g∘f)，我们考察一个旅行范畴：

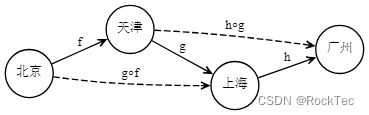
Figure 8. 旅行范畴

如上图所示，箭头的复合，就是将旅行的两步，看作一步，可以是前两步看作一步，也可以是后两步看作一步。这是自然的，态射的结合律非常直观。

因此，态射的结合律，是这种直观的公理化，即，对于任何态射 A→fB→gC→hD𝐴→𝑓𝐵→𝑔𝐶→ℎ𝐷，总有 (h∘g)∘f=h∘(g∘f)(ℎ∘𝑔)∘𝑓=ℎ∘(𝑔∘𝑓)。

对象及其性质

对象

如前所述，每个对象都必须有一个恒等态射。

如果仔细观察范畴论对对象的定义，除了这条要求，就没有别的要求了。如果我们把范畴看成是承载信息的一个载体，那么因为我们对对象除了恒等态射没有别的规定，因此该对象也不必承担特定的信息承载义务，所以对象单独拿出来，不考虑恒等态射，则它可以没有（内部）结构。

在范畴论中，对象是箭头的起点和终点，箭头通过对象标定的这些起点和终点进行连接。这是范畴论中对象的主要作用，甚至是唯一作用。即：可以把范畴看成是一个箭头的聚集，箭头的起点和终点是对象，对象可以看成点的聚集，点不包含任何信息。

恒等态射的性质

单位律

我们前面学习恒等态射时，说恒等态射是一个从对象出发，指向对象自己，不做任何其他操作的箭头。这是一种自然语言描述。我们看范畴定义中恒等态射的性质：

单位律（Unit Laws）：对于任何态射 A→fB𝐴→𝑓𝐵，总有：f∘IdA=f=IdB∘f𝑓∘𝐼𝑑𝐴=𝑓=𝐼𝑑𝐵∘𝑓

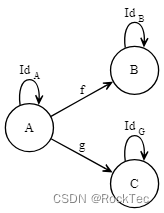
Figure 9. 恒等态射的性质

如上图所示，按照单位律，我们有：

对任何态射 A→fB𝐴→𝑓𝐵，总有：f∘IdA=f=IdB∘f𝑓∘𝐼𝑑𝐴=𝑓=𝐼𝑑𝐵∘𝑓

对任何态射 A→gC𝐴→𝑔𝐶，总有：g∘IdA=g=IdC∘g𝑔∘𝐼𝑑𝐴=𝑔=𝐼𝑑𝐶∘𝑔

... ...

这是说个什么意思？

就是说恒等箭头和任何其他箭头的复合，不会对复合结果产生影响，或者说，复合恒等箭头总是恒等于不复合恒等箭头。

恒等态射就像乘法中的1，1乘以任何数都是任何数，任何数乘以1都是任何数。

恒等态射就像加法中的0，0加任何数都是任何数，任何数加0都是任何数。

恒等箭头的验证

我们反过来考虑这一问题，比如，我们得到一个态射I，如何验证它是不是恒等态射呢？

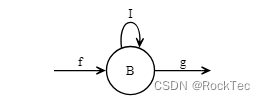
Figure 10. 恒等态射的性质

我们把任何指向B的态射（包括I），用I复合，即：I∘f，看它是不是等于f，即，检测：I∘f=f;

同时，对于任何从B发出的箭头g（包括I），我们用它来复合I，即g∘I，看它是不是等于g，即：检测：g∘I=g；

如果对于任何指向B和从B发出的态射，检测都通过，则I就是恒等态射！这反映了范畴论典型的外部观点，即我们不看f、g 和 I 具体含义如何。对于I来说，如果它参加复合和不参加复合，效果一样，那么它就是恒等态射。

这里有必要注意的是，上述描述的任何指向和发出的态射，指的是任何可能的指向和发出的态射。即，检测时必须考虑所有进入B和从B发出的所有可能的态射，包括被检测的态射自身（它既是指向B的态射，又是从B发出的态射）。这相当于说：把所有可能的检测都做一遍，如果检测成功，则I就是恒等态射。

所有可能的态射是个什么意思？我们考虑两个集合A、B，则可以定义A、B之间的函数。如果我们把集合A、B看作一个范畴中的两个对象，从A到B和从B到A的函数看成两个对象之间的态射，则所有可能的态射就是集合A、B之间所有可能定义的函数。

通常，在范畴论中我们不用去验证一个箭头是不是恒等箭头，因为对于任何对象，恒等箭头就是从一个对象出发，返回该对象的什么其他操作都不做的箭头。

但是这个恒等箭头的验证却给我们一个启示：穷尽一切可能方法，验证A’是不是A，如果全是，那么A就是A。

恒等态射的唯一性

对于一个对象，可不可能有两个不同的恒等态射呢？不可能，恒等态射必然唯一，这可以从恒等态射的单位律推出。

我们简要证明一下：

假设同一对象A有两个恒等态射Id1和Id2，它们不同，即：Id1 ≠ Id2。

显然，这两个恒等态射既是从A出发的态射，又是进入A的态射，于是按照恒等态射的性质，我们有：

把Id2看作进入的箭头，用Id1的单位性质，于是有：Id1∘Id2=Id2；对于这个得到的等式，我们用Id2的单位性质，有：Id1=Id2，然而这和我们的假设Id1 ≠ Id2矛盾。

因此 Id1 ≠ Id2 不可能，所以 Id1 = Id2。

因此恒等态射若存在，必然唯一。

而范畴论规定，恒等态射存在，所以恒等态射在范畴论中存在且唯一，即每个对象有且仅有一个恒等态射。

母范畴（Meta Category）

学习范畴论的困难在于它非常抽象，这是个什么意思？

就是说你在很多地方都可以看到范畴的具体例子，每一个例子都是范畴，但又不是范畴的全部。

这就好像我们在海边捡贝壳，我们捡到了一个扇形的贝壳，于是我们认为贝壳就是扇形的，但是另一天，我们居然捡到了一个圆形的贝壳，这让我们非常兴奋，原来，贝壳也可以是圆形的。我们信心满满，认为贝壳就应该是扇形的或者圆形的。这天，我们在海边又发现了一个椭圆形的贝壳，我们困惑了，这个圆形的家伙到底是不是贝壳？经过反复的思考，我们发现，贝壳有着更加深刻的结构和性质，这个结构和性质，并不依赖于具体的形状，虽然每个具体贝壳都有个具体的形状。

我们在本节所给出的范畴的定义，是纯公理化的，就是说，它是逻辑的起点，它 —— 并不是任何其他数学概念的推论。我们给它取个名字，叫做：Meta Category，即母范畴。您在其他的文献中，Meta Category 可能会被翻译为元范畴，但是元范畴不够通俗，而且也不够形象。叫做母范畴，我们可以采用描述法，更好地把握元范畴这个概念。

A metacategory is purely axiomatic, and does not use set theory.

母范畴是纯公理化的，它不依赖集合论。

就是说，你可以将本节定义的范畴概念，作为公理，也就是逻辑的起点来用。在该观点下，我们会看到范畴的很多具体例子，而这些例子，贯穿了很多数学问题、数学分支、数学概念和数学陈述（命题）。

母范畴的通俗描述

母范畴就像照进不可名状的世界的光线，在该光线下，无数的问题、概念、命题自然而然地诞生出来，将世界呈现为一个有形的轮廓。而分散在数学各个角落的问题、概念和陈述，不再杂乱无章，相互孤立，而是成为一个整体的一部分，这个整体就是母范畴。

母范畴是一个神奇的范畴，它将各种不同的数学分支，作为其可能特征的“化身”或“具体化”，与其相连。对各数学分支的追本溯源，我们就回归到母亲的怀抱 —— 母范畴。

反过来，当我们探索新的领域，发现问题、建立概念、陈述和命题时，母范畴就化身为这些具体的问题、概念和命题，使我们的新探索，自然成为母范畴的一部分。

以上关于母范畴的通俗描述，取法了亚历山大·格罗滕迪克（Alexander Grothendieck）的书《收获与播种》中的一些叙述方式。在学习范畴论时，我们经常会问，范畴这个概念，到底是什么？我们总是想马上搞清楚，范畴到底是什么意思，它的全部是个什么样子。

我想，上述描述是个比较好的回答，范畴是什么？它是一个母亲般的观点。

这篇关于通俗范畴论4 范畴的定义的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---