克鲁斯专题
C语言-数据结构 克鲁斯卡尔算法(Kruskal)邻接矩阵存储
相比普里姆算法来说,克鲁斯卡尔的想法是从边出发,不管是理解上还是实现上都更简单,实现思路:我们先把找到所有边存到一个边集数组里面,并进行升序排序,然后依次从里面取出每一条边,如果不存在回路,就说明可以取,否则就跳过去看下一条边。其中看是否是回路这个操作利用到了并查集,就是判断新加入的这条边的两个顶点是否在同一个集合中,如果在就说明产生回路,如果没在同一个集合那么说明没有回路可以加入
hdu-1863畅通工程 最小生成树克鲁斯卡尔算法kruskal(并查集实现)prim普利姆算法实现
畅通工程 Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 16994 Accepted Submission(s): 7134 Problem Description 省政府“畅通工程”的目标是使全省任何两个村
最小生成树——克鲁斯卡尔
克鲁斯卡尔 克鲁斯卡尔算法是实现图的最小生成树的最常用的算法,适合于求边稀疏的网。 基本思想: 设有一个有n个顶点的联通网N=(V,E),首先构造一个没有边的非联通图T=(V,E),图中每个顶点自成一个联通分量。当在E中选到具有一条最小权值的边时,若该边的两个顶点落在不同的联通分量上,则将此边加入到T中;否则将此边舍弃,重新选择一条权值最小的边,重复此过程,直到
HDU 1233还是畅通工程——克鲁斯卡尔算法(带并查集)
Problem Description 某省调查乡村交通状况,得到的统计表中列出了任意两村庄间的距离。省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通(但不一定有直接的公路相连,只要能间接通过公路可达即可),并要求铺设的公路总长度为最小。请计算最小的公路总长度。 Input 测试输入包含若干测试用例。每个测试用例的第1行给出村庄数目
数据结构之---C语言实现最小生成树之kruskal(克鲁斯卡尔)算法
//Kruskal(克鲁斯卡尔)算法//杨鑫#include <stdio.h>#include <stdlib.h>#define MAX 1000#define MAXE MAX#define MAXV MAXtypedef struct{int beginvex1; //边的起始顶点int endvex2;
最小生成树之Kruskal(克鲁斯卡尔)算法
克鲁斯卡尔算法: 是在剩下的所有未选取的边中,找最小边,如果和已选取的边构成回路,则放弃,选取次小边。 先构造一个只含 n 个顶点、而边集为空的子图,把子图中各个顶点看成各棵树上的根结点,之后,从网的边集 E 中选取一条权值最小的边, 若该条边的两个顶点分属不同的树,则将其加入子图,即把两棵树合成一棵树,反之,若该条边的两个顶点已落在同一棵树上,则不可取, 而应该取下一条权值最
克鲁斯卡尔(Kruskal)算法(K算法):公交站问题
1,应用场景—公交站问题 某城市从新增的7个站点(A,B,C,D,E,F,G),现在需要把7个站点联通各个站点的距离用边权表示,比如A-B为12公里如何修路保证各个站点都能走通,并距离最短从图和问题可以看出,克鲁斯卡尔算法与普里姆算法解决的问题完成一致,只是解决问题的方式不同 2,克鲁斯卡尔算法介绍 克鲁斯卡尔算法,是用来求加权连通图的最小生成树的算法基本算法思想:按照边权值大小从小到大
并查集与克鲁斯卡尔算法详解
并查集的常见用途:求连通子图;克鲁斯卡尔算法;求最近公共祖先 三个基本操作:(1)makeSet:建立一个新的并查集,其中包含s个单元素的集合; (2)unionSet(x,y):把元素x和y所在的集合合并,并且x,y所在的集合不相交,如果相交则不合并; (3)find(x):找到x所在的集合的代表,该操作可以用于判断两个元素是否位于同一个集合,只要比较它们各自集合的代表就可以;(什么是集合
克鲁斯CLOOS机器人维修知识分享
克鲁斯工业机器人是一种高度精密的自动化设备,广泛应用于制造业、物流等领域。为了确保机器人的正常运行,了解一些基本的CLOOS工业机械手维修知识是必不可少的。 【常见CLOOS机械臂故障及解决方法】 1. 机器人无法启动:检查电源是否正常,电源插头是否插好,保险丝是否熔断等。 2. 机器人运行不稳定:检查机械手电机、机械臂减速机、机器人驱动部件等是否正常工作。 3. 机器人碰撞保护:检查安全防护装置
最小生成树之克鲁斯卡尔(kruskal)算法
#include <iostream> #include <string> using namespace std; typedef struct MGraph{ string vexs[10];//顶点信息 int arcs[10][10];//邻接矩阵 int vexnum, arcnum;//顶点数和边数 }MGraph; int LocateVex(MGraph G,
Hdu1233 step6.1.4还是畅通工程(克鲁斯卡尔)
Hdu1233 step6.1.4还是畅通工程 Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 22072 Accepted Submission(s): 9855 Problem Description
Hdu1232 step6.1.3畅通工程(克鲁斯卡尔)
Hdu1232 step6.1.3畅通工程 Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 25531 Accepted Submission(s): 13332 Problem Description 某
成都克鲁斯机器人电路板故障维修攻略,快来了解一下!
一、克鲁斯机器人电路板维修步骤 断开电源:在进行电路维修前,务必断开机器人的电源,确保安全。 拆卸电路板:根据电路图或维修手册,小心拆卸故障电路板。注意记录拆卸过程中的细节,以便后续重新安装。 更换损坏元件:使用万用表等工具测试克鲁斯机器人电路板上的元件,找出损坏的元件并进行更换。注意选择与原件相匹配的型号和规格,确保更换后的元件能够正常工作。 修复焊接点:检查电路板上的焊接点,如有虚焊或脱焊现象
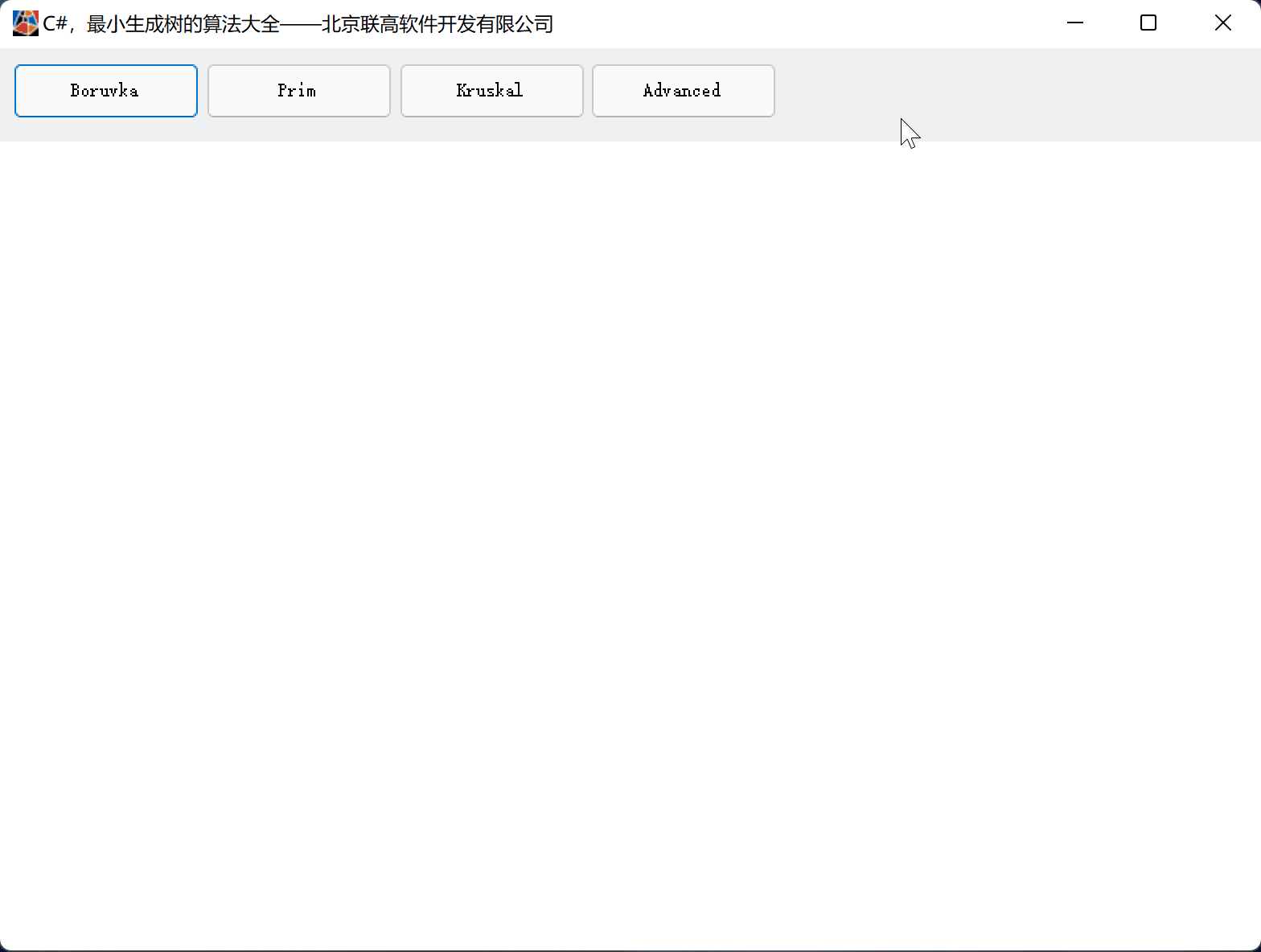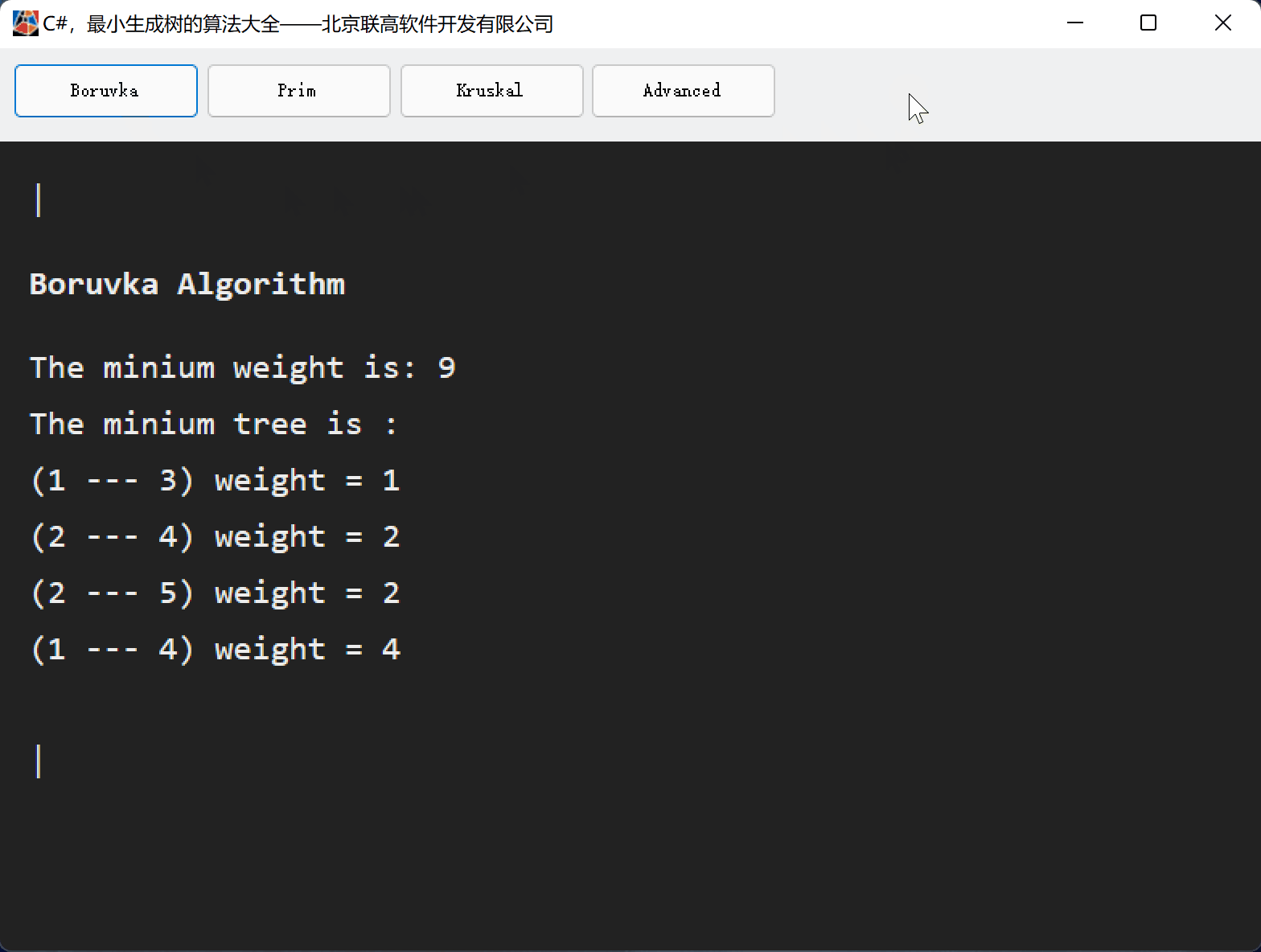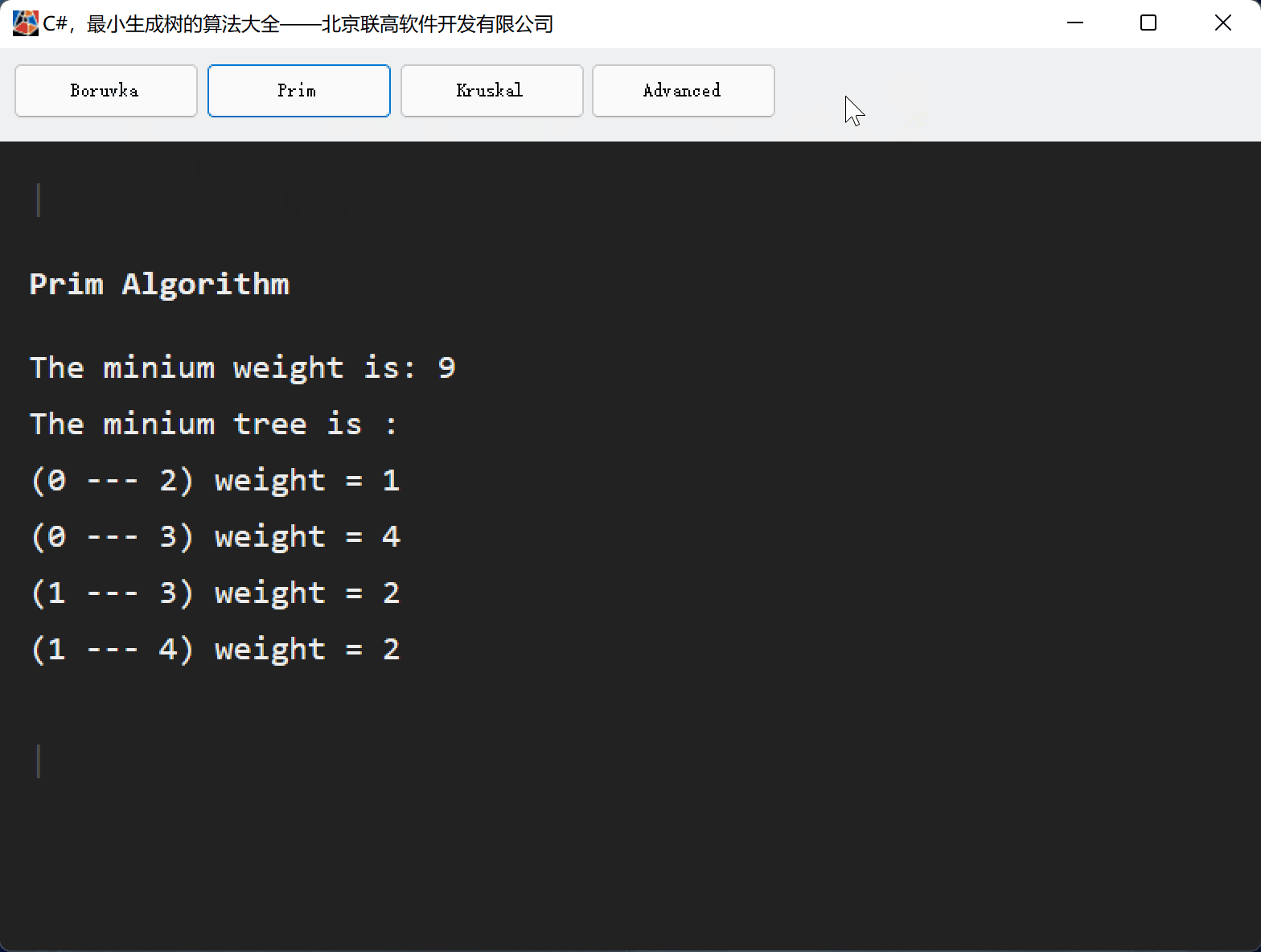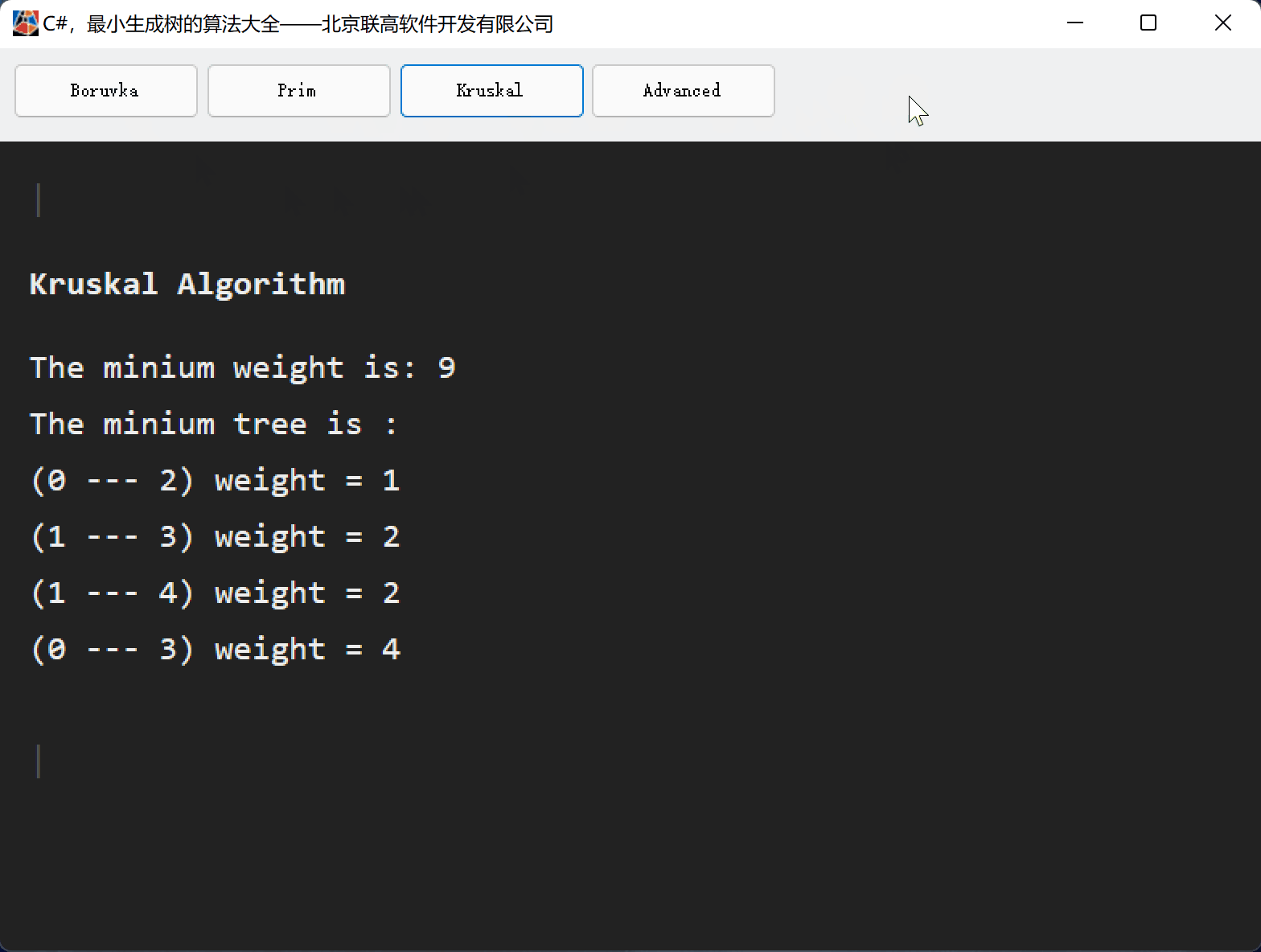
C#,最小生成树(MST)克鲁斯卡尔(Kruskal)算法的源代码
一、Kruskal算法简史 克鲁斯卡尔(Kruskal)算法是一种用来寻找最小生成树的算法,由Joseph Kruskal在1956年发表。用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪婪算法的应用。和Boruvka算法不同的地方是,Kruskal算法在图中存在相同权值的边时也有效。 二、Kruskal算法思路 (1)记Graph中有v个顶点,e个
普利姆(prim)算法和克鲁斯卡尔(kruskal)算法
连通网的最小生成树算法: 1.普里姆算法——”加点法”。 假设N=(V,{E})是连通网,TE为最小生成树的边集合。 (1)初始U={u0}(u0∈V),TE=φ; (2)在所有u∈U, v∈V-U的边(u,v)中选择一条代价最小的边(u0,v0)并入集合TE,同时将v0并入U;(并修正U-V中各顶点到U的最短边信息) (3)重复步骤(2),直到U=V为止。 此时,TE中含有n-1
克鲁斯卡尔-最小生成树
最小生成树实际意义在于解决一张图里面,把所有顶点用最短路径全部连接 第三次人工智能浪潮 看了杨澜的节目,才继续坚持写,人工智能需要好的算法,是先人们几辈的积累和爆发 我们要抓住这个时代。 克鲁斯卡尔算法,最小生成树,插边,适合边少,稀疏 借助两个数组,一个(se[]) 用来存放已经按照权值从小到大排完序的表 一个(set[])用来存放顶点属于哪一个集合,刚开始初始化所有顶点独占一个集合
最小生成树和普利姆算法及克鲁斯卡尔算法
一、最小生成树的介绍 最小生成树(Minimum Cost Spanning Tree), 简称 MST。即给定一个带权的无向连通图,如何选取一棵生成树,使树上所有边上权的总和为最小,这叫最小生成树 给定一个带权的无向连通图,如何选取一棵生成树,使树上所有边上权的总和为最小,这叫最小生成树N个顶点,一定有N-1条边包含全部顶点求最小生成树的算法主要是普里姆算法和克鲁斯卡尔算法 二、
两种最小生成树的方法——普里姆算法、克鲁斯卡尔算法
目录 一、最小生成树的概念 二、MST性质 1、性质 2、 证明 二、普里姆(Prim)算法 1、算法思想 2、图形解析 3、逐步实现 (1)建立无向图的邻接矩阵 (2)找出辅助数组中与closedge代价最小的顶点的位置 (3)普里姆核心算法 4、总代码 5、时间复杂度 三、克鲁斯卡尔(Kruskal)算法 1、算法思想 2、图形解析 3、逐步实现 (1)构建
再遇最小生成树(普里姆,普里姆+堆优化,克鲁斯卡尔)
生成树概念: 任何只由图G的边构成,并包含所有顶点的树称为G的生成树 最小生成树概念:最小生成树是其所有生成树中权重最小的生成树 算法区别 普里姆算法:普里姆算法贪的是点,适用于点少边多的稠密图,从不在点集合S的点中选出一个点,假设选出的点是j,我们让他与S内的某点距离最短,这样我们选出了一条生成树上的边,同时将点j加入S中,不断重复这个过程,直到所有点都加入点集合S。 克鲁斯卡尔算法:克鲁
彻底搞懂克鲁斯卡尔(Kruskal)算法(附C++代码实现)
一.问题 图中的6个顶点分别代表6个村庄,线段的权值代表村庄之间的距离。请问如何找到最短的路径来访问每一个村庄,且每个村庄只访问一次。 二.解决 1.提取图的边,并将边按权值大小从小到大排列,并放入edge数组。如下: 2.创建根数组(辅助数组),数组下标代表顶点节点本身,其元素代表顶点的根节点,如下: 提示:这里的“根”并不是树结构中真正的根,一棵树中只有一个根,而这
学习笔记|多独立样本秩和检验|克鲁斯卡尔-沃利斯检验|多个组间的多重比较|规范表达|《小白爱上SPSS》课程:SPSS第十四讲 | 多独立样本秩和检验如何做?
目录 学习目的软件版本原始文档多独立样本秩和检验一、实战案例读数据: 二、统计策略三、SPSS操作1、正态性检验2、多个独立样本的秩和检验3、多个组间的多重比较 四、结果解读第一,描述性统计结果。 第二 ,给出的是不同训练年限各自的样本量和平均秩。第三,给出的是Kruskal-Wallis H检验的统计量、自由度、和渐进显著性。第四,表4分别进行6次多重比较 五、规范报告1、规范表格2、规范
java实现克鲁斯卡尔算法
应用背景 某城市新增7个站点(A,B,C,D,E,F,G) ,现在需要修路把7个站点连通各个站点的距离用边线表示(权),比如A~B距离12公里问:如何修路保证各个站点都能连通,并且总的修建公路总里程最短? 克鲁斯卡尔算法介绍 克鲁斯卡尔(Kruskal)算法,是用来求加权连通图的最小生成树的算法。基本思想: 按照权值从小到大的顺序选择n-1条边,并保证这n-1条边不构成回路具体做法: 首
克鲁斯卡尔算法(Kruskal)
克鲁斯卡尔(Kruskal)算法是一种按权值的递增次序选择合适的边来构造最小生成树的方法。假设 G=(V,E) G=(V,E)是一个具有 n n个顶点的带权连通图,T=(U,TE)T=(U,TE)是 G G的最小生成树,则构造最小生成树的步骤如下: 1) 设置UU的初值等于 V V(即包含有GG中的全部顶点), TE TE的初值为空集(即图 T T中每一个顶点都构成一个分量)。 2) 将图G