本文主要是介绍克鲁斯卡尔算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

连通图中寻找最小生成树的常用算法有 2 种,分别是普里姆算法和克鲁斯卡尔算法。本节,我们将带您详细了解克鲁斯卡尔算法。
和普里姆算法类似,克鲁斯卡尔算法的实现过程也采用了贪心的策略:对于具有 n 个顶点的图,将图中的所有路径(边)按照权值大小进行升序排序,从权值最小的路径开始挑选,只要此路径不会和已选择的其它路径构成环路,就选定其作为最小生成树的一部分,直至选够 n-1 条路径。
对于具有 n 个顶点的图,选择 n-1 条路径就可以将所有顶点连接起来。在此基础上,保证所选的每条路径的权值都最小,就可以找到一棵最小生成树。

以图 1 所示的连通图为例,克鲁斯卡尔算法寻找最小生成树的过程为:
1) 将所有路径(边)按照权值大小进行升序排序:

2) 从最小的路径开始,只要该路径不会和其它已选路径产生环路,就选择它作为组成最小生成树的一部分。显然 (B,D) 符合要求,选择它组成最小生成树:
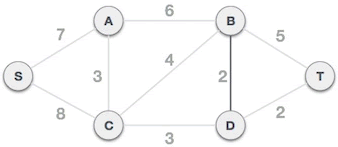
3) (D,T) 不会和已选路径 (B,D) 构成环路,可以组成最小生成树:
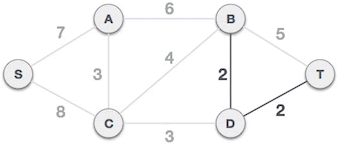
4) (A,C) 不会和 (B,D)、(D,T) 构成环路,可以组成最小生成树:

5) (C,D) 不会和 (A,C)、(B,D)、(D,T) 构成环路,可以组成最小生成树:

6) (C,B) 会和已选路径 (C,D)、(B,D) 构成环路(如图 6 所示),因此不会被选择:
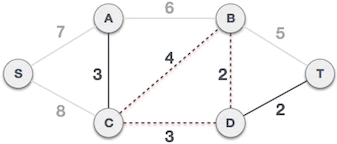
7) (B,T) 会和已选路径 (B,D)、(D,T) 构成环路,也不被选择;
8) (A,B) 会和已选路径 (A,C)、(C,D)、(D,B) 构成环路,也不被选择;
9) (S,A) 不会和已选路径 (A,C)、(C,D)、(D,B)、(D,T) 构成环路,可以组成最小生成树:
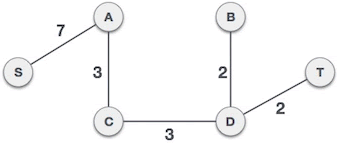
克鲁斯卡尔算法的具体实现
克鲁斯卡尔算法的实现,难点在于如何判断所选路径是否会造成环路,这里给您介绍一种简单的解决方案:初始状态下,为图中的每个顶点配备一个互不相同的标记值,算法执行过程中,如果新路径两个顶点的标记值不同,则不会构成环路,该路径被选择的同时,要将两个顶点的标记改为和其它已选路径中的顶点标记相同;反之,如果该路径两个顶点的标记值相同,则会构成环路。
举个例子,图 5 中,已选路径为 (A,C)、(B,D)、(C,D)、(D,T),此时顶点 A、C、B、D、T 的标记值相同,顶点 S 的标记值和它们不同。图 6 中,判定 (B,C) 路径是否可以组成最小生成树时,由于顶点 B 和 C 的标记值相同,因此该路径会和其它已选路径构成环路(如图 6 所示),不能组成最小生成树。
如下为实现克鲁斯卡尔算法的 C 语言程序:
#include <stdio.h> #include <stdlib.h> #define N 9 // 图中边的数量 #define P 6 // 图中顶点的数量 //构建表示边的结构体 struct edge {//一条边有 2 个顶点int initial;int end;//边的权值int weight; }; //qsort排序函数中使用,使edges结构体中的边按照权值大小升序排序 int cmp(const void *a, const void*b) {return ((struct edge*)a)->weight - ((struct edge*)b)->weight; } //克鲁斯卡尔算法寻找最小生成树,edges 存储用户输入的图的各个边,minTree 用于记录组成最小生成树的各个边 void kruskal_MinTree(struct edge edges[], struct edge minTree[]) {int i,initial, end;//每个顶点配置一个标记值int assists[P];int num = 0;//初始状态下,每个顶点的标记都不相同for (i = 0; i < P; i++) {assists[i] = i;}//根据权值,对所有边进行升序排序qsort(edges, N, sizeof(edges[0]), cmp);//遍历所有的边for (int i = 0; i < N; i++) {//找到当前边的两个顶点在 assists 数组中的位置下标initial = edges[i].initial - 1;end = edges[i].end - 1;//如果顶点位置存在且顶点的标记不同,说明不在一个集合中,不会产生回路if (assists[initial] != assists[end]) {//记录该边,作为最小生成树的组成部分minTree[num] = edges[i];//计数+1num++;int elem = assists[end];//将新加入生成树的顶点标记全部改为一样的for (int k = 0; k < P; k++) {if (assists[k] == elem) {assists[k] = assists[initial];}}//如果选择的边的数量和顶点数相差1,证明最小生成树已经形成,退出循环if (num == P - 1) {break;}}} } void display(struct edge minTree[]) {int cost = 0;printf("最小生成树为:\n");for (int i = 0; i < P - 1; i++) {printf("%d-%d 权值:%d\n", minTree[i].initial, minTree[i].end, minTree[i].weight);cost += minTree[i].weight;}printf("总权值为:%d", cost); } int main() {int i;struct edge edges[N], minTree[P - 1];for (i = 0; i < N; i++) {scanf("%d %d %d", &edges[i].initial, &edges[i].end, &edges[i].weight);}kruskal_MinTree(edges,minTree);display(minTree);return 0; }
这篇关于克鲁斯卡尔算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









