本文主要是介绍并查集与克鲁斯卡尔算法详解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
并查集的常见用途:求连通子图;克鲁斯卡尔算法;求最近公共祖先
三个基本操作:(1)makeSet:建立一个新的并查集,其中包含s个单元素的集合;
(2)unionSet(x,y):把元素x和y所在的集合合并,并且x,y所在的集合不相交,如果相交则不合并;
(3)find(x):找到x所在的集合的代表,该操作可以用于判断两个元素是否位于同一个集合,只要比较它们各自集合的代表就可以;(什么是集合的代表)?
实现:用树来表示集合,树的每个结点就表示集合中的一个元素,树根对应的元素就是该集合的代表。
树的结点表示集合中的元素,指针表示指向父节点的指针,根结点的指针指向自己,表示其没有父节点。沿着每个节点的父节点不断向上查找,最终就可以找到根结点,也就是该集合的代表元素;
makeSet:就是建立一个数组,并赋初值,利用循环;
find 操作:如果每次都沿着父节点向上查找,那么时间复杂度就是树的高度,不可能达到常数级;
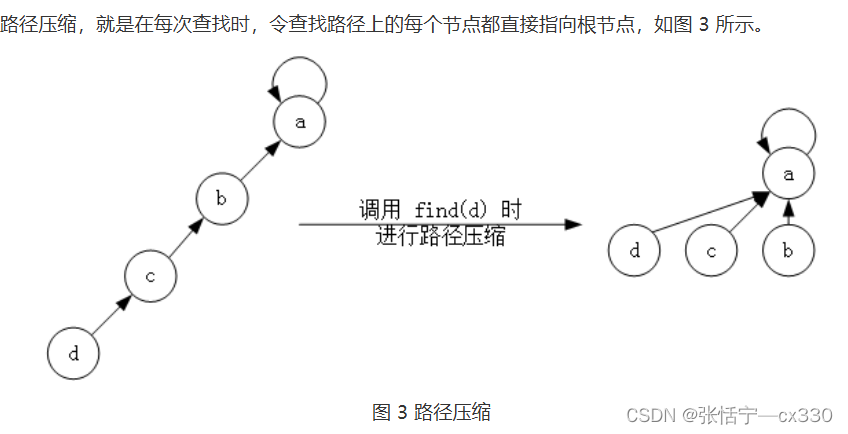
我们在这里需要采用一种策略:——路径压缩
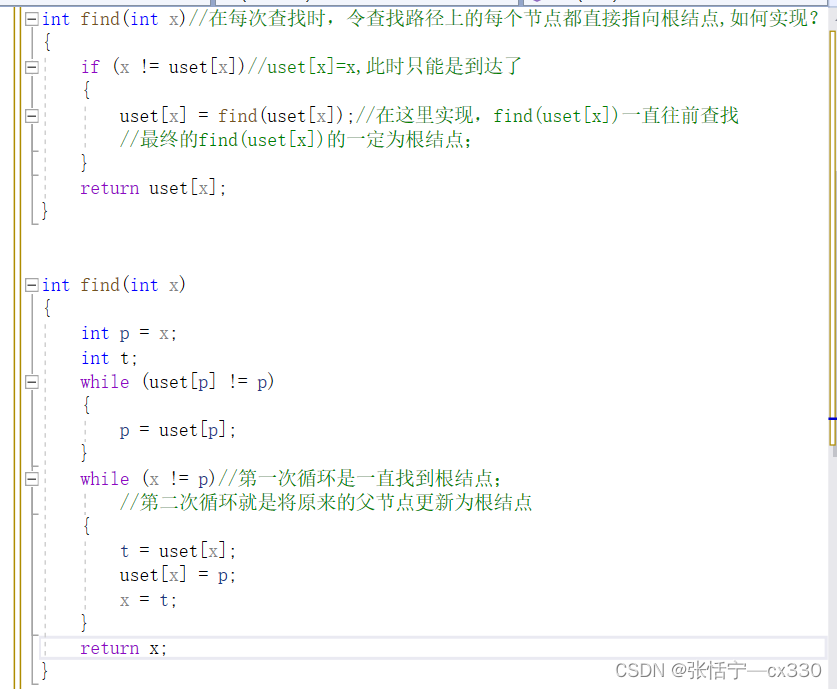
路径压缩就体现在将所有的节点的父亲节点都变为根结点;
unsionSet操作:并查集的合并,就是将一个集合的树根指向另一个集合的树根;
合并的原则:按秩合并,使用秩来表示树高度的上界,在合并时,总是将具有较小秩的树根指向具有较大秩的树根,简单的说就是总是将比较矮的树作为子树,添加到较高的树中,为了保存秩,需要额外使用一个与uset同长度的数组,并将所有的元素都初始化为0;//这个秩不太好理解;
第二种方式:按集合中包含的元素个数(或者说树中的节点数)合并,将包含节点较少的树根,指向包含节点较多的树根。这个策略与按秩合并的策略类似,同样可以提升并查集的运行速度,而且省去了额外的 rank 数组。
这样的并查集具有一个略微不同的定义,即若 uset 的值是正数,则表示该元素的父节点(的索引);若是负数,则表示该元素是所在集合的代表(即树根),而且值的相反数即为集合中的元素个数。相应的代码如下所示,同样包含递归和非递归的 find 操作:
这里不需要设立rank数组;
void UFset() // 初始化{for (int i = 0; i < n; i ++)parent[i] = -1;}int Find(int x) // 查找并返回结点x所属集合的根结点{int s; // 查找位置for (s = x; parent[s]>=0; s = parent[s]); // 注意这里的 ;while (s != x) // 优化方案 -- 压缩路径,使后续的查找{int tmp = parent[x];parent[x] = s;x = tmp;}return s;}// R1和R2是两个元素,属于两个不同的集合,现在合并这两个集合void Union (int R1, int R2){// r1位R1的根结点,r2位R2的根结点int r1 = Find(R1), r2 = Find(R2);int tmp = parent[r1] + parent[r2]; // 两个集合的结点个数之和(负数)//每添加一个节点,就将其parent更新为tmp,也就意味着其个数增加1;//一个边对应两个点,每次只对两个点进行操作,所以可以加1;只更新顶点的parent,//一开始是所有的顶点都可以作为集合的代表// 如果R2所在树结点个数 > R1所在树结点个数// 注意parent[r1]和parent[r2]都是负数if(parent[r1] > parent[r2]) // 优化方案 -- 加权法则{parent[r1] = r2; // 将根结点r1所在的树作为r2的子树(合并)parent[r2] = tmp; // 跟新根结点r2的parent[]值}else{parent[r2] = r1; // 将根结点r2所在的树作为r1的子树(合并)parent[r1] = tmp; // 跟新根结点r1的parent[]值}}二.克鲁斯卡尔算法
最小生成树之克鲁斯卡尔(Kruskal)算法 - gaoyanliang - 博客园 (cnblogs.com)


但是其实并查集只是按照顺序加边,没有比较边的权值这一过程,所以如果我们按照边的值从小到达进行排列的话,我们就只需要前面几条较小的边就能将所有的节点连接起来,最终得到最小的生成树;
sort函数的实现:根据cmp的结果,设置:是否交换
//在C语言中:利用qsort函数,直接对edge类型的数组中的weigjt进行排序;
#include <stdio.h> #include <stdlib.h> // 假设edges是一个整数数组,我们要根据整数的大小进行排序 int cmpfunc(const void *a, const void *b){ return (*(int*)a - *(int*)b); } int main() { int edges[] = {3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5}; int m = 5; // 假设我们只想对前5个元素进行排序 // 注意:qsort会排序整个数组,但我们可以通过调整传入的元素数量来限制它的范围// 由于qsort没有直接的“开始索引”和“结束索引”参数,我们通常传递整个数组,但只在比较函数中处理我们关心的部分// 如果我们真的只想对前m个元素进行排序,并且这些元素之后的数据我们不想改变, // 那么我们需要复制前m个元素到一个新数组,对新数组进行排序,然后再复制回去。 // 但这里为了简单起见,我们直接对整个数组进行排序。// 使用qsort进行排序 qsort(edges, sizeof(edges) / sizeof(edges[0]), sizeof(int), cmpfunc); // 打印排序后的数组 for(int i = 0; i < sizeof(edges) / sizeof(edges[0]); i++) { printf("%d ", edges[i]); } return 0; }在这里u,v表示的时一个边的两个顶点//——体现加边法这一特点;
因此在for循环中,循环的次数最多的给的是m——即为图的边数,而不是顶点数,区别于普利姆算法;
直到所有的顶点都加入到了一个集合中;
所以只要把并查集搞清楚,就能很容易地实现克鲁斯卡尔算法。
这篇关于并查集与克鲁斯卡尔算法详解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






