克鲁斯卡尔（Kruskal）算法（K算法）：公交站问题

本文主要是介绍克鲁斯卡尔（Kruskal）算法（K算法）：公交站问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1，应用场景—公交站问题

• 某城市从新增的7个站点（A，B，C，D，E，F，G），现在需要把7个站点联通
• 各个站点的距离用边权表示，比如A-B为12公里
• 如何修路保证各个站点都能走通，并距离最短
• 从图和问题可以看出，克鲁斯卡尔算法与普里姆算法解决的问题完成一致，只是解决问题的方式不同

2，克鲁斯卡尔算法介绍

• 克鲁斯卡尔算法，是用来求加权连通图的最小生成树的算法
• 基本算法思想：按照边权值大小从小到大的顺序选取n - 1条边，并保证这n - 1条边不构成回路
• 回路的判断标准是连接边的两个顶点的终点重合

2.1，算法图解

1. 以应用场景中的左图为例

2. 第一步，取最小的边，即<E，F>，权值为2
   

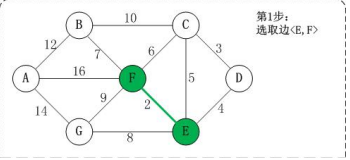
3. 第二步，继续取最小的边，即<C，D>，权值为3
   

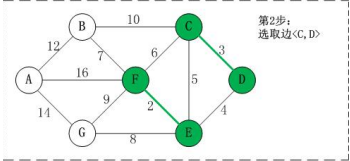
4. 第三步，继续取<D，E>，此处注意，构成回路的标准是顶点的终点不能一致，不是按照顶点的访问记录判断
   

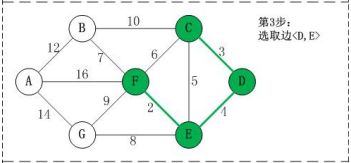
5. 紧接着，取最小的边<C，E>，此处注意，<C，E>构成了回路；因为将<E，F>，<C，D>，<D，E>加入到最小生成树中后，这几个边的顶点<C，D，E，F>就都了各自的终点F，此时再连接<C，E>时，<C，E>的终点都为F，终点重合，则构成了回路，不能构建

6. 按照第一步到第五步的逻辑，依次类推，则最后的结果如下：
   

7. 此时，最小生成树构建完成，最后的结果是<E，F>，<C，D>，<D，E>，<B，F>，<E，G>，<A，B>

3，代码实现

package com.self.datastructure.algorithm.kruskal;import lombok.AllArgsConstructor;
import lombok.Data;
import lombok.Getter;import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;/*** 克鲁斯卡尔算法* * 克鲁斯卡尔算法与Prim算法解决问题完全一致, 只是解决问题的方式不同* * 不同于Prim算法以点为基本单位, 克鲁斯卡尔以边为基本单位* * 先构建问题图表, 构建顶点, 并从中读取边的集合(注意不要读取两份)* * 然后对边按大小进行升序排列* * 遍历边的集合, 依次取出最小的边, 参与最小生成树的生成* * 分别从顶点-终点的记录数组中取出该边对应两个顶点的终点* * 如果终点重合说明构成了回路, 则不能构建* * 终点不重合, 说明还没有连接, 则继续构建* * 边集合遍历完成后, 整个最小生成树构建也随之完成* * 注意: 此处不能通过顶点已经访问来统计, 比如ABCD四个顶点, AB构成, CD构成, 此时ABCD已经全部访问, 但是不连通* @author pj_zhang* @create 2020-07-11 12:12**/
public class Kruskal {private final static int NOT_CONN = Integer.MAX_VALUE;public static void main(String[] args) {// 顶点集合char[] lstVertex = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};// 连接关系int[][] vertexMap = {{0, 12, NOT_CONN, NOT_CONN, NOT_CONN, 16, 14},{12, 0, 10, NOT_CONN, NOT_CONN, 7, NOT_CONN},{NOT_CONN, 10, 0, 3, 5, 6, NOT_CONN},{NOT_CONN, NOT_CONN, 3, 0, 4, NOT_CONN, NOT_CONN},{NOT_CONN, NOT_CONN, 5, 4, 0, 2, 8},{16, 7, 6, NOT_CONN, 2, 0, 9},{14, NOT_CONN, NOT_CONN, NOT_CONN, 8, 9, 0}};// 构建图MyGraph myGraph = new MyGraph(lstVertex, vertexMap);// 进行克鲁斯卡尔计算MyEdge[] result = kruskal(myGraph);System.out.println("最终结果如下: ");for (MyEdge myEdge : result) {System.out.println(myEdge);}}/*** 进行克鲁斯卡尔算法计算* @param myGraph 图表* @return 返回最终的连接关系*/private static MyEdge[] kruskal(MyGraph myGraph) {// 结果集, 边的数量为顶点数量-1MyEdge[] result = new MyEdge[myGraph.getLstVertex().length - 1];int index = 0; // 记录下标位置// 顶点的连接终点集合, 初始化为0int[] endArr = new int[myGraph.getLstVertex().length];// 获取边集合MyEdge[] lstEdges = myGraph.getLstEdges();// 对边按权值从小到大进行排序sortEdges(lstEdges);// 对边集合进行遍历, 从最小开始取边进行最小生成树构建for (MyEdge myEdge : lstEdges) {// 获取边开始和结束的顶点char startVertex = myEdge.getStart();char endVertex = myEdge.getEnd();// 获取顶点对应的下标int startIndex = getVertexIndex(myGraph, startVertex);int endIndex = getVertexIndex(myGraph, endVertex);// 获取顶点连接串的终点, 避免构成回路int startEnd = getEndIndex(endArr, startIndex);int endEnd = getEndIndex(endArr, endIndex);// 如果终点值不重合, 说明不会构成回路, 则进行连接if (startEnd != endEnd) {// 对终点的终点进行延伸endArr[startEnd] = endEnd;// 记录边result[index++] = myEdge;}}System.out.println("终点数组: " + Arrays.toString(endArr));return result;}/*** 获取顶点的终点索引* @param endArr 终点记录数组* @param index 当前顶点下标* @return 终点下标*/private static int getEndIndex(int[] endArr, int index) {// 如果当前顶点存在终点, 则继续去找终点的终点// 找到最终点, 最终返回该索引while (endArr[index] != 0) {index = endArr[index];}// 如果当前顶点的终点为0, 表示顶点的终点就是它自己, 直接返回即可return index;}/*** 获取顶点对应的下标* @param myGraph 图* @param vertex 顶点* @return*/private static int getVertexIndex(MyGraph myGraph, char vertex) {for (int i = 0; i < myGraph.getLstVertex().length; i++) {if (myGraph.getLstVertex()[i] == vertex) {return i;}}return -1;}/*** 对边按权值进行排序* @param lstEdges*/private static void sortEdges(MyEdge[] lstEdges) {for (int i = 0; i < lstEdges.length; i++) {for (int j = 0; j < lstEdges.length - 1 - i; j++) {if (lstEdges[j].getWeight() > lstEdges[j + 1].getWeight()) {MyEdge temp = lstEdges[j];lstEdges[j] = lstEdges[j + 1];lstEdges[j + 1] = temp;}}}}/*** 构建图表*/@Getterstatic class MyGraph {/*** 顶点数量*/private int vertexCount;/*** 顶点列表*/private char[] lstVertex;/*** 顶点图*/private int[][] vertexMap;/*** 顶点的边集合*/private MyEdge[] lstEdges;public MyGraph(char[] lstVertex, int[][] vertexMap) {this.vertexCount = lstVertex.length;this.lstVertex = lstVertex;this.vertexMap = vertexMap;// 记录边, 按顺序读取, 保证顺序List<MyEdge> lstData = new ArrayList<>(10);for (int i = 0; i < vertexCount; i++) {// 从下一位开始读, 保证不会生成重复的边for (int j = i + 1; j < vertexCount; j++) {// 如果连接, 则进行统计if (vertexMap[i][j] != NOT_CONN) {lstData.add(new MyEdge(lstVertex[i], lstVertex[j], vertexMap[i][j]));}}}lstEdges = new MyEdge[lstData.size()];for (int i = 0; i < lstData.size(); i++) {lstEdges[i] = lstData.get(i);}}}/*** 边对象*/@Data@AllArgsConstructorstatic class MyEdge {/*** 起点*/private char start;/*** 终点*/private char end;/*** 权重*/private int weight;}}

这篇关于克鲁斯卡尔（Kruskal）算法（K算法）：公交站问题的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---