假设检验专题
Spark Mllib之相关性计算和假设检验
Spark Mllib之相关性计算和假设检验 原创: 小小虫 一、皮尔逊相关性和斯皮尔曼相关性 1.1 皮尔逊相关性 要理解 Pearson 相关系数,首先要理解协方差(Covariance)。协方差表示两个变量 X,Y 间相互关系的数字特征,其计算公式为: Pearson 相关系数公式如下: 由公式可知,Pearson 相关系数是用协方差除以两个变
概率统计Python计算:假设检验应用——分布拟合检验
对来自总体 X X X的样本 X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn,及给定的显著水平 α \alpha α检验假设 H 0 : X 的分布函数为 F ( x ) ( H 1 : X 的分布函数不是 F ( x ) ) . H_0:X\text{的分布函数为}F(x)(H_1:X\text{的分布函数不是}F(x)). H0:X
概率统计Python计算:假设检验应用——基于成对数据的检验
设有 n n n个相互独立的观测结果 ( X 1 , Y 1 ) (X_1,Y_1) (X1,Y1), ( X 2 , Y 2 ) (X_2,Y_2) (X2,Y2), ⋯ \cdots ⋯, ( X n , Y n ) (X_n,Y_n) (Xn,Yn),诸对 X i X_i Xi和 Y i Y_i Yi受同一因素影响, D i = X i − Y i D_i=X_i-Y_i
数据分析:假设检验方法汇总及R代码实现
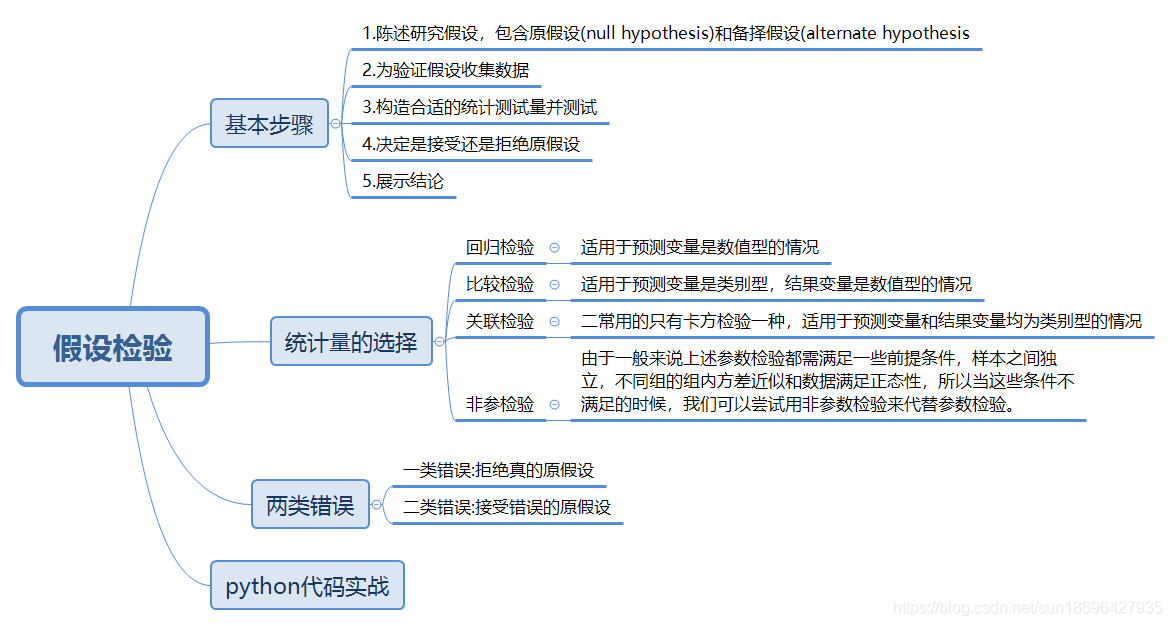
欢迎大家关注全网生信学习者系列: WX公zhong号:生信学习者Xiao hong书:生信学习者知hu:生信学习者CDSN:生信学习者2 介绍 显著性检验方法,通常也被称为假设检验方法,是统计学中用于评估样本统计量是否显著不同于某个假设值的一种重要工具。以下是假设检验方法使用时需要考虑的三个条件的书面化表述: 一、数据分组数目(处理组数目)的考虑 在进行假设检验时,首先需要考虑的是数
python数据分析--- ch12-13 python参数估计与假设检验
python数据分析--- ch12-13 python参数估计与假设检验 1. Ch12--python 参数估计1.1 参数估计与置信区间的含义及函数版1.1.1 参数估计与置信区间的含义1.1.2 参数估计函数版1.1.3 参数估计函数版 1.2 Python单正态总体均值区间估计1.2.1 方差 σ 2 \sigma^2 σ2已知1.2.2 方差 σ 2 \sigma^2 σ2未知
【概率论】第八章 假设检验
假设检验 一、假设检验1.1 假设检验的原理1.2 假设检验中的重要概念 二、正态总体参数的假设验证2.1 单个总体的参数的检验2.2 两个正态总体参数的假设检验 一、假设检验 1.1 假设检验的原理 1.2 假设检验中的重要概念 二、正态总体参数的假设验证 2.1 单个总体的参数的检验 2.2 两个正态总体参数的假设检验
从零开始统计学 01 | 假设检验
文章目录 一、提出假设二、选择检验方法2.1 正态分布2.2 t分布(*t-distribution*)与T检验2.3 F分布(*F-distribution*)与方差分析2.4 卡方分布 (*chi-square distribution*)与卡方检验2.4.1 检验数据是否服从某种分布2.4.1.1 使用绘图2.4.1.2 使用卡方检验2.4.1.3 使用Kolmogorov-Smirn
杂记——假设检验中p值的理解
p p p值是拒绝零假设的显著性水平的最小的 α \alpha α值,对于一切大于 p p p值的 α \alpha α,错误拒绝 H 0 H_0 H0的概率不超过 α \alpha α。 p p p值是利用实际调查或实验数据,通过代入抽样分布计算出的一个概率值,如果原假设是正确的,那么 p p p值不应该较小。而如果很小,说明小概率事件经常发生,就有悖原假设,就要拒绝。
数理统计复习笔记五——假设检验之显著性检验
一、基本概念 在统计中,我们把需要用样本去推断“正确”与否的命题称为一个假设。当然,假设是可以关于参数的,也可以是关于分布的。 通过样本对一个假设作出“对”或“不对”的具体判断规则就称为该假设的一个检验。检验的结果若“是”,则否定该命题,就称拒绝该假设,否则就称为接受原假设。这里的拒绝和接受原假设,只是在当前样本下作出的判断,并没有从逻辑或理论上“证明”该命题正确与否。 设有样本 X X X
对于假设检验的个人理解
1 P与α的关系 P是实际的最小犯错误概率,α是可容忍的最小犯错误概率(设定好的),若可容忍的最小犯错误概率比实际的大,故实际是可以犯错误的,犯第一类错误,拒绝原假设(若实际最小犯错误概率<可容忍最小犯错误概率,则可以犯错误,犯第一类错误,拒绝原假设),总之P<α拒绝原假设。 2 统计学上P值大于0.05数据符合正态分布 原假设为无差异,P>0.05表明与正态分布无差异,故符合正态分布。
假设检验(hypothesis testing)及P值(p-value)
前一篇t检验的文末提到了P值的概念,P值实际上是医学统计中很常用的一个概念,那么这篇文章继续讲解什么是P值。说到P值,就得先从假设检验说起。 首先声明,此篇的内容是来自"马同学高等数学"微信公众号的内容。 目录 1、什么是假设检验 2、P值 2.1 为什么要把更极端的情况加起来? 3、显著水平 4、与置信区间的关系 参考文献: 1、什么是假设检验 抛硬币是概率
手把手教你使用Python实现常用的假设检验 !
开门见山。 这篇文章,教大家用Python实现常用的假设检验! 服从什么分布,就用什么区间估计方式,也就就用什么检验! 比如:两个样本方差比服从F分布,区间估计就采用F分布计算临界值(从而得出置信区间),最终采用F检验。 建设检验的基本步骤: 前言 假设检验用到的Python工具包 Statsmodels是Python中,用于实现统计建模和计量经济学的工具包,主要包括描述统计、统计模型估计
【小白学机器学习12】假设检验之3:t 检验 (t检验量,t分布,查t值表等)
目录 1 t 检验的定义 1.1 来自维基百科和百度百科 1.2 别名 1.3 和其他检验的区别 2 适用情况: 2.1 关于样本情况 2.2 适合检查的情况 2.2.1 单样本均值检验(One-sample t-test) 2.2.2 两独立样本均值检验(Independent two-sample t-test) 2.2.3 配对样本均值检验(Dependent t-te
python统计分析——统计学假设检验和统计学建模
参考资料:python统计分析【托马斯】 对于大部分统计问题,我们可以从两个角度来看:可以做一个假设,并证实或证伪;或是建立一个统计模型,并分析模型参数的显著性。我们用经典的t检验做例子进行介绍: 1、t检验 假设我们在两种不同场景下对一个赛车对的表现进行衡量。代码如下: # 导入库import numpy as npfrom scipy import
假设检验|第三章:统计学中的显著性水平α和P
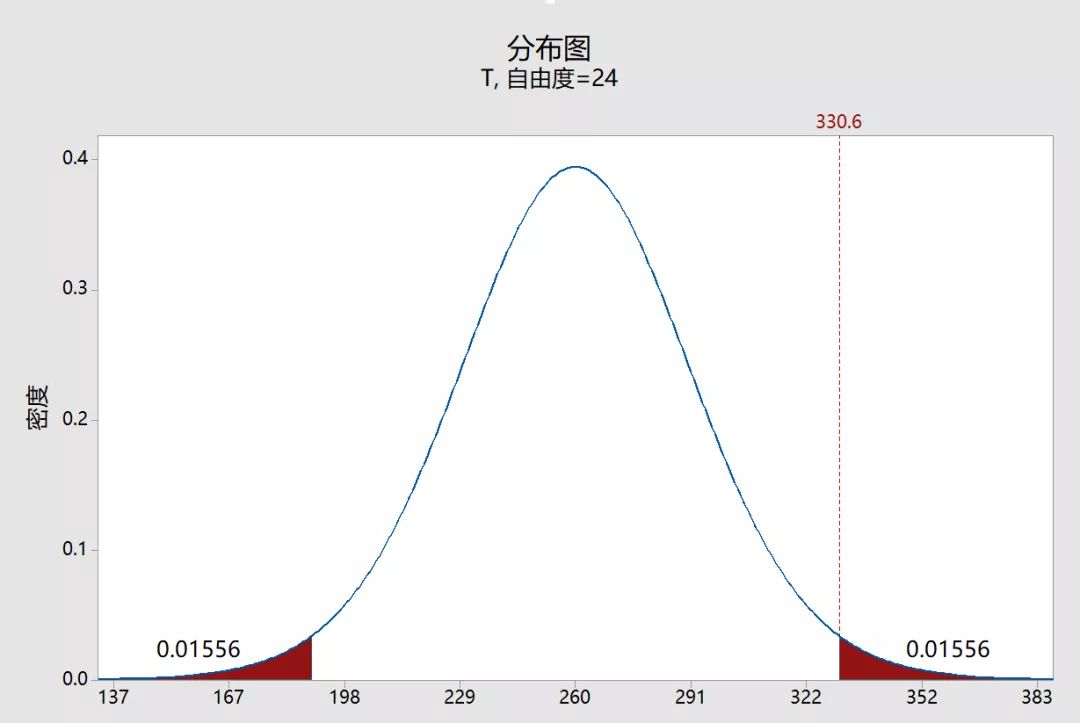
文章来自微信公众号:发现Minitab 概述 在假设检验中,我们很多时候对显著性水平α和P值理解不透彻?在这篇文章中,我将继续关注概念和图形,以帮助您更直观地理解假设检验在统计学中的工作原理。 为了实现它,我将在我之前文章的基础上将显著性水平α和P值添加到图形中,以便执行单样本t检验。当您可以看到真正意义上的统计意义时,您会更容易理解! 在上一篇文章中我们想确定我们的样本平均值(330.6)是否
【知识管理】假设检验pvalue的计算
让我们通过一个具体的例子来解释P值的计算过程,假设我们有一个模型用于区分SCD(亚临床痴呆)和HC(健康对照)的分裂。我们通过置换测试来计算模型性能的P值。 原始模型性能评估 首先,我们在原始数据集上运行模型。假设我们关注的性能指标是准确率,模型在原始数据集上的准确率为80%。 置换测试步骤 打乱标签:我们将原始数据集中的标签(SCD和HC)随机打乱,这样数据和标签之间的真实关联被破坏。
A/B测试--假设检验实例
本文将主要介绍假设检验的三个类型: 单样本检验 相关配对检验 独立双样本检验 一、假设检验的步骤 1.提出问题? 根据实际问题,建立零假设、备选假设分别为H0和H1。H0和H1互为相反,不可能同时满足。检验类型:单样本检验、相关配对检验、独立双样本检验抽样分布类型(正态分布、t分布、其他分布) 当样本容量n>=30,无论总体为何分布,均值的抽样分布均为正态分布,即中心极限定理。 当样本容量n<
《统计学简易速速上手小册》第4章:假设检验(2024 最新版)
文章目录 4.1 假设检验的基本概念4.1.1 基础知识4.1.2 主要案例:新饮料偏好测试4.1.3 拓展案例 1:教育方法的效果比较4.1.4 拓展案例 2:工作满意度调查 4.2 常见的假设检验4.2.1 基础知识4.2.2 主要案例:产品包装改进的效果评估4.2.3 拓展案例 1:新课程教学效果的评价4.2.4 拓展案例 2:不同营销策略的效果比较 4.3 假设检验的应用4.3.
R假设检验之Breusch-Godfrey检验(Breusch-Godfrey Test)
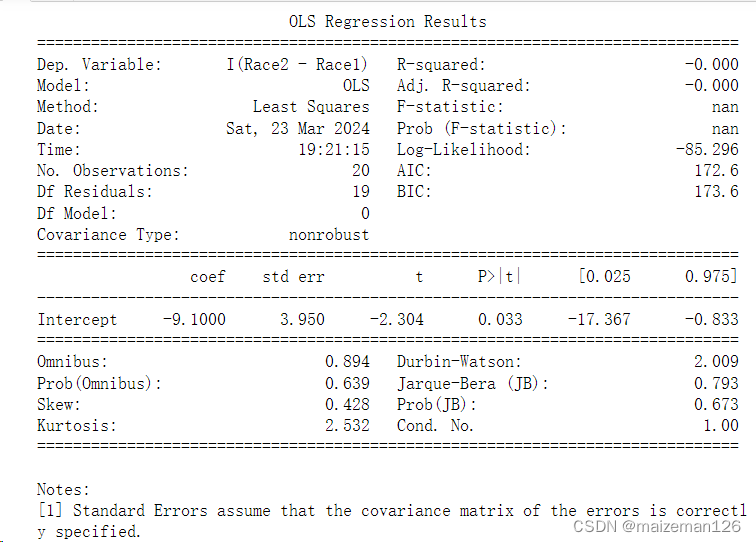
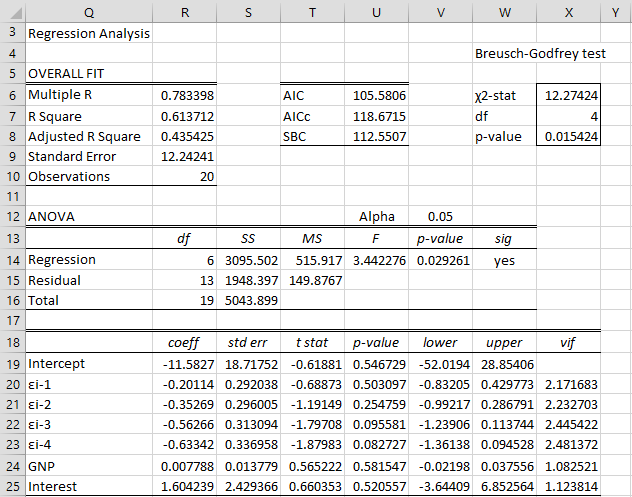
R假设检验之Breusch-Godfrey检验(Breusch-Godfrey Test) 线性回归中的一个关键假设是残差之间不存在相关性,即残差是独立的。 为了测试一阶自相关,我们可以执行Durbin-Watson检验。然而,如果我们想测试高阶的自相关(autocorrelation),那么我们需要执行一个Breusch-Godfrey检验。 Breusch-God
aic值检验 p值_参数估计和假设检验
前言:所谓统计推断,就是利用样本所提供的信息对总体的某些统计特征进行估计或者判断,进而认识总体。统计推断分为两大类:参数估计,假设检验。 1 .参数估计 参数估计和假设检验是统计推断的基本内容,几乎所有统计建模的PROC步都会设计参数估计以及相对应的假设检验。假设总体 的分布函数的类型已知,但其中一个或者多个参数未知,那么就需要对这些未知的参数做出合理的估计,并且对估计做出评价,这