数据分析：假设检验方法汇总及R代码实现

本文主要是介绍数据分析：假设检验方法汇总及R代码实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

欢迎大家关注全网生信学习者系列：

WX公zhong号：生信学习者
Xiao hong书：生信学习者
知hu：生信学习者
CDSN：生信学习者2

介绍

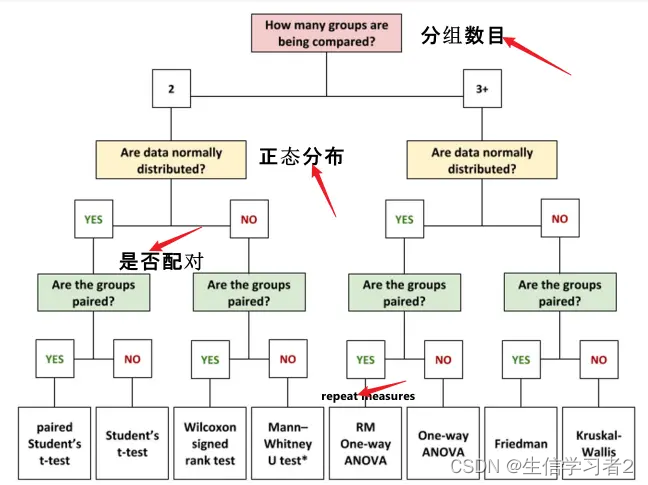
在这里插入图片描述

显著性检验方法，通常也被称为假设检验方法，是统计学中用于评估样本统计量是否显著不同于某个假设值的一种重要工具。以下是假设检验方法使用时需要考虑的三个条件的书面化表述：

一、数据分组数目（处理组数目）的考虑

在进行假设检验时，首先需要考虑的是数据的分组数目，尤其是处理组的数量。通常，我们以2为阈值进行初步判断。当处理组数目为2时（例如，实验组与对照组的比较），可以采用适用于两组数据的检验方法，如独立样本t检验或Mann-Whitney U检验（取决于数据的分布情况）。当处理组数目超过2时，可能需要采用多组比较的检验方法，如方差分析（ANOVA）或Kruskal-Wallis H检验。

二、数据的分布类型判断

数据的分布类型对于选择合适的假设检验方法至关重要。如果数据符合正态分布（或近似正态分布），通常可以选择参数检验方法，因为这类方法基于总体的已知或假设的分布参数进行推断。常见的参数检验方法包括t检验、z检验、方差分析（ANOVA）等。然而，如果数据不符合正态分布，则应该选择非参数检验方法，因为它们不依赖于总体的具体分布形式。常见的非参数检验方法包括Mann-Whitney U检验、Wilcoxon秩和检验、Kruskal-Wallis H检验等。

三、数据是否为配对数据的考量

数据的配对性也是选择假设检验方法时需要考虑的因素之一。配对数据指的是两组数据之间存在一一对应关系的数据，如同一样本在不同时间或不同条件下的测量值。对于配对数据，可以采用配对样本t检验或Wilcoxon符号秩检验等方法进行比较。这些方法能够充分利用配对数据之间的相关性，提高检验的效率和准确性。如果数据不是配对的，则应该选择独立样本的检验方法。

加载R包

knitr::opts_chunk$set(message = FALSE, warning = FALSE)library(tidyverse)
library(SummarizedExperiment)
library(ggpubr)

导入数据

本次使用配对的血清蛋白质组学数据作为案例数据，该数据可通过下列链接下载：

百度云盘链接: https://pan.baidu.com/s/1FM5JZIH2MsGhuDGo-yCvtA
提取码: 请关注WX公zhong号_生信学习者_后台发送 检验方法数据 获取提取码

long_se_protein <- readRDS("Zeybel_2022_plasma_protein_se_Paired.RDS")long_se_protein

#> class: SummarizedExperiment 
#> dim: 72 42 
#> metadata(0):
#> assays(1): ''
#> rownames(72): IL8 VEGFA ... TNFB CSF_1
#> rowData names(3): Protein ID LOD prop
#> colnames(42): P101001_After P101001_Before ...
#>   P101077_After P101077_Before
#> colData names(49): SampleID PatientID ...
#>   Right_leg_fat_free_mass Right_leg_total_body_water

每组样本的数目 (配对分组：Mild， Moderate， Severe)

with(colData(long_se_protein) %>% data.frame(), table(Stage, LiverFatClass))

#>         LiverFatClass
#> Stage    Mild Moderate None Severe
#>   After     5        7    2      7
#>   Before    6        7    0      8

数据探索

准备假设检验所需要的数据和数据探索。

准备数据

不配对的两组数据
配对的两组数据
三组数据

profile <- assay(long_se_protein) %>%as.data.frame()
metadata <- colData(long_se_protein) %>%as.data.frame()# 两组不配对数据
metadata_2_unpaired <- metadata %>%dplyr::filter(Stage == "Before") %>%dplyr::filter(LiverFatClass %in% c("Mild", "Moderate"))
profile_2_unpaired <- profile[, pmatch(rownames(metadata_2_unpaired), colnames(profile)), F]
merge_2_unpaired <- metadata_2_unpaired %>%dplyr::select(SampleID, LiverFatClass) %>%dplyr::inner_join(profile_2_unpaired %>% t() %>%as.data.frame() %>%tibble::rownames_to_column("SampleID"),by = "SampleID")# 两组配对数据
metadata_2_paired <- metadata %>%dplyr::filter(LiverFatClass == "Moderate")
profile_2_paired <- profile[, pmatch(rownames(metadata_2_paired), colnames(profile)), F]
merge_2_paired <- metadata_2_paired %>%dplyr::select(SampleID, PatientID, Stage) %>%dplyr::inner_join(profile_2_paired %>% t() %>%as.data.frame() %>%tibble::rownames_to_column("SampleID"),by = "SampleID") %>%dplyr::filter(!SampleID %in% c("P101052_After", "P101052_Before"))# 三组数据
metadata_3_unpaired <- metadata %>%dplyr::filter(Stage == "Before") %>%dplyr::filter(LiverFatClass %in% c("Mild", "Moderate", "Severe"))
profile_3_unpaired <- profile[, pmatch(rownames(metadata_3_unpaired), colnames(profile)), F]
merge_3_unpaired <- metadata_3_unpaired %>%dplyr::select(SampleID, LiverFatClass) %>%dplyr::inner_join(profile_3_unpaired %>% t() %>%as.data.frame() %>%tibble::rownames_to_column("SampleID"),by = "SampleID")

正态性评估

数据正态性评估是统计学中的一种方法，用于判断一组数据是否遵循正态分布（又称高斯分布）。正态分布是一种连续概率分布，其图形呈现为对称的钟形曲线，具有以下特点：

对称性：数据分布的图形是对称的，以均值为中心。
均值、中位数和众数相等：在正态分布中，这三个统计量是相等的。
68-95-99.7规则：在正态分布中，约68%的数据值落在均值的±1个标准差范围内，约95%的数据值落在均值的±2个标准差范围内，约99.7%的数据值落在均值的±3个标准差范围内。

正态性评估的常用方法包括：

直方图：通过绘制数据的直方图来观察其分布形状。
Q-Q图（Quantile-Quantile Plot）：将数据的分位数与正态分布的理论分位数进行比较，如果数据点近似落在一条直线上，则数据接近正态分布。
描述性统计：检查数据的均值、中位数、标准差等统计量。
正态性检验：如Kolmogorov-Smirnov检验、Shapiro-Wilk检验、Anderson-Darling检验等，这些检验可以给出一个p值，帮助判断数据是否来自正态分布。

可视化探索: density plot 密度图提供了一个关于分布是否呈钟形(正态分布)的直观判断

ggdensity(merge_2_unpaired$IL8, main = "Density plot of IL8",xlab = "IL8")

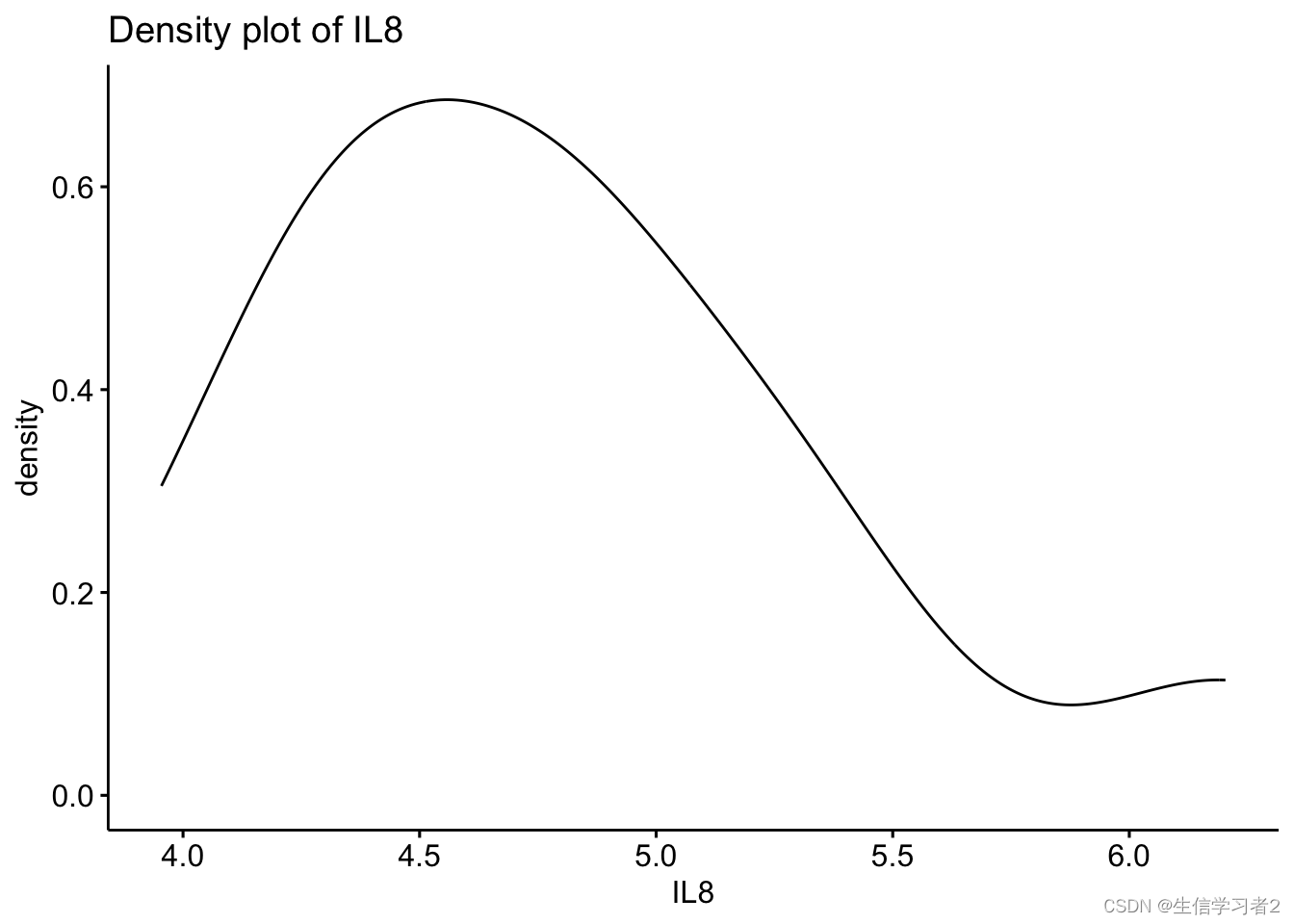
在这里插入图片描述

可视化探索: histogram 如果直方图大致呈“钟形”，则假定数据为正态分布

gghistogram(merge_2_unpaired$IL8, main = "Density plot of IL8",xlab = "IL8")

在这里插入图片描述

可视化探索: Q-Q plot Q-Q图描绘了给定样本与正态分布之间的相关性

ggqqplot(merge_2_unpaired$IL8, main = "Density plot of IL8",xlab = "IL8")

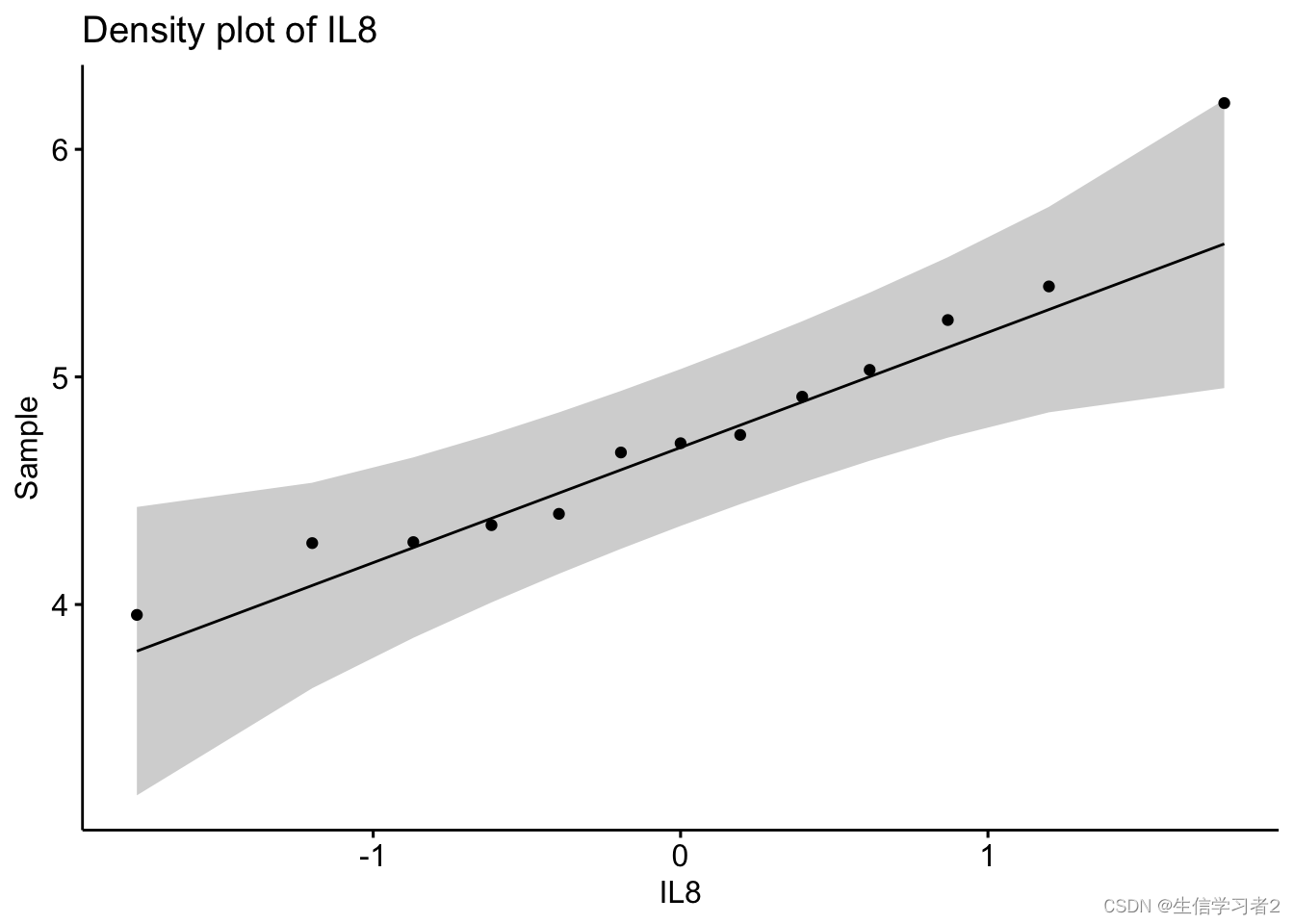
在这里插入图片描述

正态检验: shapiro.test提供单变量的正态分性检验方法（Shapiro-Wilk test）

If the p-value of the test is greater than α = 0.05, then the data is assumed to be normally distributed.

shapiro.test(merge_2_unpaired$IL8)

#> 
#>  Shapiro-Wilk normality test
#> 
#> data:  merge_2_unpaired$IL8
#> W = 0.93269, p-value = 0.3694

正态检验: ks.test提供单变量的正态分性检验方法（Kolmogorov-Smirnov test）

If the p-value of the test is greater than α = 0.05, then the data is assumed to be normally distributed.

ks.test(merge_2_unpaired$IL8,"pnorm")

#> 
#>  Exact one-sample Kolmogorov-Smirnov test
#> 
#> data:  merge_2_unpaired$IL8
#> D = 0.99996, p-value = 2.22e-16
#> alternative hypothesis: two-sided

结果：第二次检验的p值小于0.05，说明IL8数据不是正态分布。

Shapiro-Wilk检验和Kolmogorov-Smirnov（K-S）检验都是用于评估数据是否来自某个特定分布的统计检验，但它们在某些方面存在差异：

Shapiro-Wilk检验：这是一种非常敏感的正态性检验，特别适用于小到中等大小的样本（通常小于50）。它检验的是数据是否来自正态分布。
Kolmogorov-Smirnov检验：这是一种通用的检验，用于比较样本分布与任何连续分布（不仅限于正态分布）。K-S检验检验的是样本分布与理论分布（在这种情况下是正态分布）之间的最大差异。

当Shapiro-Wilk检验的p值大于0.05时，我们没有足够的证据拒绝数据来自正态分布的零假设。然而，当K-S检验的p值小于0.05时，我们有证据拒绝零假设，表明样本分布与正态分布存在显著差异。

出现这种矛盾的情况可能有以下几个原因：

样本大小：Shapiro-Wilk检验对小样本更敏感，而K-S检验对大样本更敏感。如果样本量较大，K-S检验可能更容易检测到小的偏差。
检验的敏感性：Shapiro-Wilk检验被认为是评估正态性的“黄金标准”，因为它对正态性的偏差非常敏感。K-S检验可能对某些类型的偏差更敏感，而对其他类型的偏差不太敏感。
数据的特性：数据可能具有某些特征，使得Shapiro-Wilk检验认为它们足够接近正态分布，而K-S检验则检测到了与正态分布的显著差异。

在面对这种矛盾的情况时，可以考虑以下几个步骤：

检查数据：重新检查数据的直方图和Q-Q图，以直观评估数据的分布形状。
考虑样本大小：如果样本量较大，可能需要更谨慎地解释K-S检验的结果。
使用其他检验：考虑使用其他正态性检验，如Anderson-Darling检验或Lilliefors检验，以获得更多信息。
综合判断：综合考虑所有检验的结果和数据的可视化图形，做出最终判断。如果大多数检验都表明数据不是正态分布，那么可能需要考虑数据转换或使用非参数方法。

非正态数据转换方法

当给定的数据集不符合正态分布时，可以采用以下数学转换方法来改善其正态性：

对数转换（Log Transformation）：对数据集中的每个值 𝑥 应用自然对数函数，即 log⁡(𝑥)。这种转换可以减少数据的偏斜性，尤其是当数据具有正偏态（右偏）时。
平方根转换（Square Root Transformation）：对数据集中的每个值 𝑥应用平方根函数，即 𝑥。这通常用于处理计数数据或具有轻微正偏态的数据。
立方根转换（Cube Root Transformation）：对数据集中的每个值 𝑥应用立方根函数，即 𝑥^1/3。这种转换有助于减少数据的偏斜性，并且比平方根转换对极端值的影响更小。

Paired student’s t-test

配对T检验（Paired T-test），也称为重复测量T检验或相关样本T检验，用于比较两组相关或配对的数据。这种检验适用于以下情况：

数据是配对的：每对数据来自于同一受试者或对象，例如，同一个受试者在不同时间点的测量结果。
数据是正态分布：两组数据都应近似正态分布，或者样本量足够大（通常认为大于30）时，根据中心极限定理，样本均值的分布将近似正态分布。

配对T检验的计算步骤如下：

计算差异分数：对于每一对数据，计算第一个测量值与第二个测量值的差值
计算差异分数的均值。
计算差异分数的标准差。
计算t统计量。
确定显著性水平：选择一个显著性水平，如 𝛼=0.05。
查找t分布的临界值：根据自由度（通常是 𝑛−1）和显著性水平，查找t分布表中的临界值。
做出结论：如果计算出的t统计量大于临界值，则拒绝零假设，认为两组数据之间存在显著差异。

在这里插入图片描述

R基础函数t.test

t.test(IL8 ~ Stage, data = merge_2_paired, paired = TRUE, alternative = "two.sided")

#> 
#>  Paired t-test
#> 
#> data:  IL8 by Stage
#> t = 0.13325, df = 5, p-value = 0.8992
#> alternative hypothesis: true mean difference is not equal to 0
#> 95 percent confidence interval:
#>  -0.566393  0.628323
#> sample estimates:
#> mean difference 
#>        0.030965

rstatix提供的t_test()

library(rstatix)stat.test <- merge_2_paired  %>% t_test(IL8 ~ Stage, paired = TRUE, detailed = TRUE) %>%add_significance()stat.test

#> # A tibble: 1 × 14
#>   estimate .y.   group1 group2    n1    n2 statistic     p
#>      <dbl> <chr> <chr>  <chr>  <int> <int>     <dbl> <dbl>
#> 1   0.0310 IL8   After  Before     6     6     0.133 0.899
#> # ℹ 6 more variables: df <dbl>, conf.low <dbl>,
#> #   conf.high <dbl>, method <chr>, alternative <chr>,
#> #   p.signif <chr>

结果: 根据本次统计分析的结果，p值等于0.899，大于设定的显著性水平0.05。因此，我们没有足够的证据拒绝零假设，即认为IL8在实验前后没有表现出统计学上的显著差异。另外，为了进一步评估实验效应的实际意义，我们计算了效应量 (平均值和方差的比值：d = mean/SD)。效应量是一个量化指标，用于衡量两个比较组之间差异的大小，或者变量之间的关联强度。它不受样本大小的影响，因此可以提供关于效应实际重要性的额外信息。

merge_2_paired %>% cohens_d(IL8 ~ Stage, paired = TRUE)

#> # A tibble: 1 × 7
#>   .y.   group1 group2 effsize    n1    n2 magnitude 
#> * <chr> <chr>  <chr>    <dbl> <int> <int> <ord>     
#> 1 IL8   After  Before  0.0544     6     6 negligible

可视化上述结果

stat_label <- stat.test %>% add_xy_position(x = "Stage")ggpaired(merge_2_paired, x = "Stage", y = "IL8", order = c("Before", "After"),ylab = "IL8", xlab = "Stage",fill = "Stage") + stat_pvalue_manual(stat_label, tip.length = 0) +labs(subtitle = get_test_label(stat_label, detailed = TRUE))

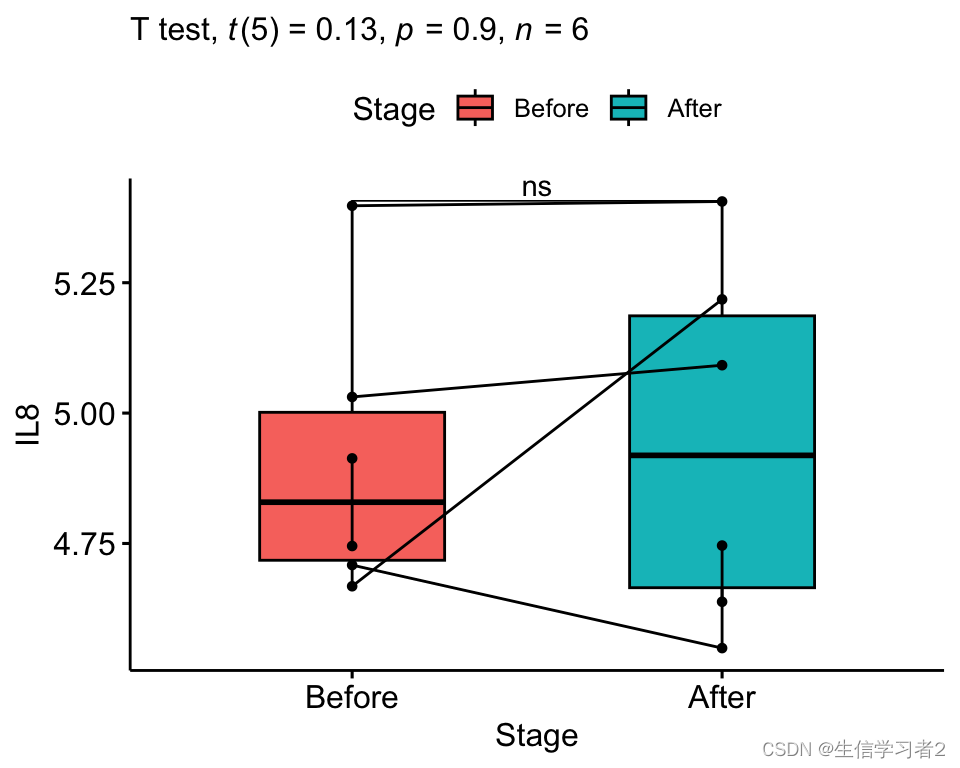
在这里插入图片描述

Student’s t-test

普通T检验，也称为独立样本T检验或两样本T检验，适用于比较两组独立数据的均值差异。这种检验的前提条件是两组数据都是正态分布的，并且具有相同的方差（方差齐性）。

在满足正态性和方差齐性的条件下，我们计算了两组数据的均值和标准差，然后计算T统计量。

计算得到的T统计量将用于与T分布的临界值进行比较，以确定两组数据的均值差异是否具有统计学意义。如果T统计量的绝对值大于临界值，或者相应的p值小于显著性水平（例如0.05），则我们拒绝零假设，认为两组数据的均值存在显著差异。

t.test(IL8 ~ LiverFatClass, data = merge_2_unpaired, paired = FALSE, alternative = "two.sided")stat.test <- merge_2_unpaired  %>% t_test(IL8 ~ LiverFatClass, paired = FALSE, detailed = TRUE) %>%add_significance()
# stat.test

#> 
#>  Welch Two Sample t-test
#> 
#> data:  IL8 by LiverFatClass
#> t = -0.32904, df = 6.193, p-value = 0.753
#> alternative hypothesis: true difference in means between group Mild and group Moderate is not equal to 0
#> 95 percent confidence interval:
#>  -1.0116344  0.7702116
#> sample estimates:
#>     mean in group Mild mean in group Moderate 
#>               4.716680               4.837391

merge_2_unpaired %>% cohens_d(IL8 ~ LiverFatClass, paired = FALSE)

#> # A tibble: 1 × 7
#>   .y.   group1 group2   effsize    n1    n2 magnitude 
#> * <chr> <chr>  <chr>      <dbl> <int> <int> <ord>     
#> 1 IL8   Mild   Moderate  -0.188     6     7 negligible

可视化结果

stat_label <- stat.test %>% add_xy_position(x = "LiverFatClass")ggboxplot(merge_2_unpaired, x = "LiverFatClass", y = "IL8", order = c("Mild", "Moderate"),ylab = "IL8", xlab = "LiverFatClass",fill = "LiverFatClass") + stat_pvalue_manual(stat_label, tip.length = 0) +labs(subtitle = get_test_label(stat_label, detailed = TRUE))

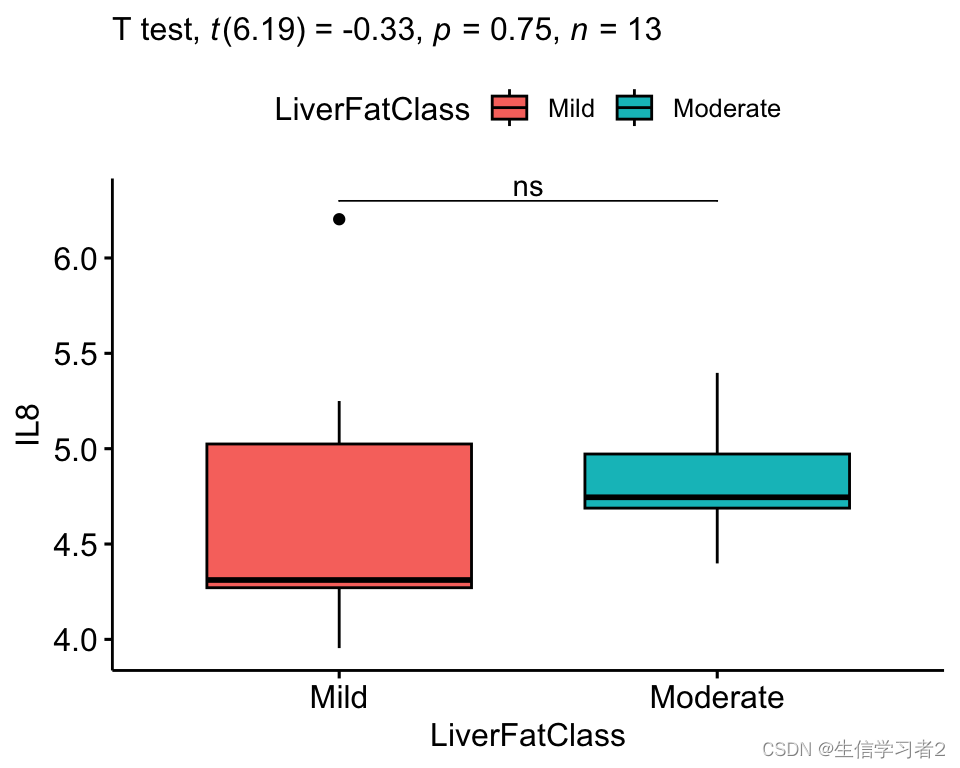
在这里插入图片描述

Wilcoxon signed rank t-test

配对Wilcoxon检验，也称为符号秩检验或Wilcoxon符号等级检验，是一种非参数统计方法，适用于比较两组配对数据的差异。与配对T检验不同，配对Wilcoxon检验不对数据的分布形态做出正态分布的假设。

配对Wilcoxon检验不要求数据遵循特定的分布，如正态分布。因此，它对于偏态分布或非对称分布的数据同样适用。检验的步骤如下：

计算差异分数：对于每一对数据，计算第一次测量与第二次测量的差值。
确定符号和等级：将差值按照其符号（正或负）进行分类，并为非零差值分配等级（秩次），等级越高表示差值的绝对值越大。
计算检验统计量：计算较小差值（正或负）的秩和 𝑇。如果存在零差值，将其排除在秩和计算之外。
确定检验统计量的临界值：根据样本量和使用的显著性水平，查找配对Wilcoxon检验的临界值表。
做出结论：如果计算出的秩和 𝑇小于或等于临界值，或者相应的p值小于显著性水平（例如0.05），则我们拒绝零假设，认为两组配对数据之间存在显著差异。

R基础函数wilcox.test

wilcox.test(IL8 ~ Stage, data = merge_2_paired, paired = TRUE, alternative = "two.sided")

#> 
#>  Wilcoxon signed rank exact test
#> 
#> data:  IL8 by Stage
#> V = 12, p-value = 0.8438
#> alternative hypothesis: true location shift is not equal to 0

rstatix提供的wilcox_test()

library(rstatix)stat.test <- merge_2_paired  %>% wilcox_test(IL8 ~ Stage, paired = TRUE, detailed = TRUE) %>%add_significance()stat.test

#> # A tibble: 1 × 13
#>   estimate .y.   group1 group2    n1    n2 statistic     p
#>      <dbl> <chr> <chr>  <chr>  <int> <int>     <dbl> <dbl>
#> 1   0.0401 IL8   After  Before     6     6        12 0.844
#> # ℹ 5 more variables: conf.low <dbl>, conf.high <dbl>,
#> #   method <chr>, alternative <chr>, p.signif <chr>

Mann-Whitney U test

Mann-Whitney U检验，也称为Wilcoxon秩和检验，是一种非参数统计检验方法，用于比较两个独立样本的中心趋势是否存在显著差异。这种检验不依赖于数据的分布形态，适用于不符合正态分布的样本，或者样本量较小的情况。以下是Mann-Whitney U检验的基本步骤：

计算秩和：分别计算两个样本的秩和，即每个样本中所有数据点的等级之和。
计算U统计量：使用以下公式计算两个样本的U统计量。
确定检验统计量：选择较小的U值作为检验统计量，因为Mann-Whitney U检验是基于U值的绝对值来确定显著性的。
确定显著性水平：选择一个显著性水平，如 𝛼=0.05。
查找临界值：根据样本量和显著性水平，查找Mann-Whitney U检验的临界值表。
做出结论：如果计算出的U值小于或等于临界值，或者相应的p值小于显著性水平，则拒绝零假设，认为两个样本的中心趋势存在显著差异。

Mann-Whitney U检验是一种灵活的统计方法，特别适用于以下情况：

数据不满足正态分布的假设。
样本量较小。
数据是有序分类数据或等级数据。

A Mann-Whitney U test (sometimes called the Wilcoxon rank-sum test) is used to compare the differences between two independent samples when the sample distributions are not normally distributed and the sample sizes are small (n <30).

wilcox.test(IL8 ~ LiverFatClass, data = merge_2_unpaired, paired = FALSE, alternative = "two.sided")

#> 
#>  Wilcoxon rank sum exact test
#> 
#> data:  IL8 by LiverFatClass
#> W = 13, p-value = 0.2949
#> alternative hypothesis: true location shift is not equal to 0

可视化

ggplot(merge_2_unpaired, aes(x = LiverFatClass, y = IL8)) + geom_boxplot(width=0.3) +stat_summary(fun = mean, geom = "point", col = "black") +  stat_summary(fun = mean, geom = "text", col = "black", size = 3, vjust = 3, aes(label = paste("Mean:", round(after_stat(y), digits = 2)))) +xlab("LiverFatClass") +ylab("IL8") +theme_bw()

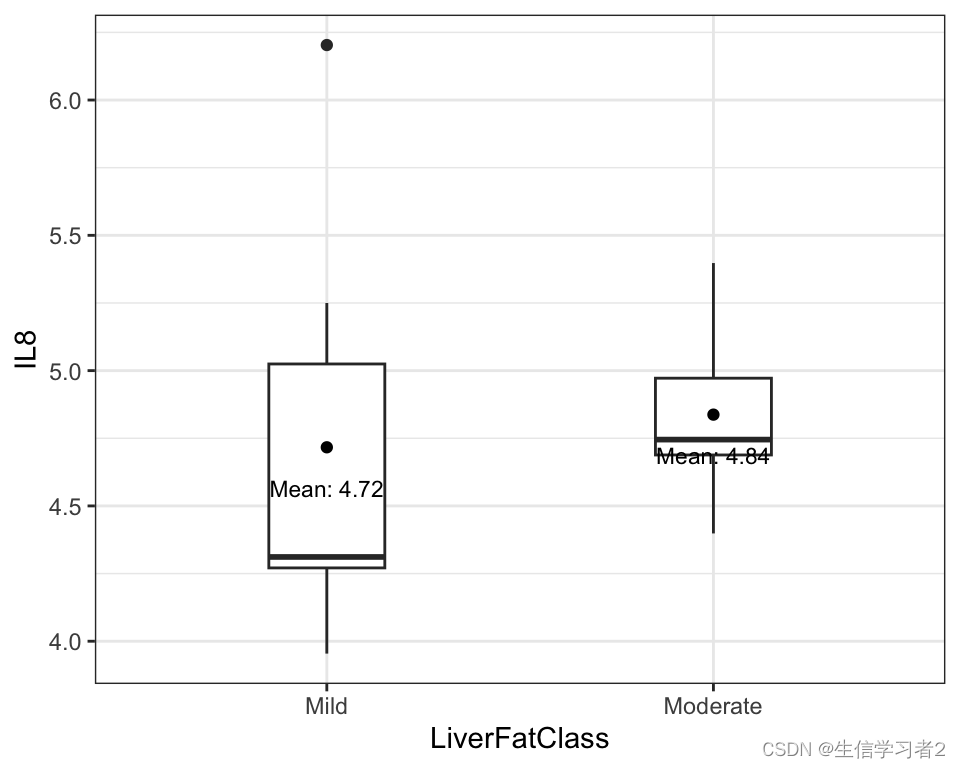
在这里插入图片描述

Repeated measures One-way ANOVA

重复测量单因素方差分析是一种统计方法，用于分析一个或多个受试者在不同时间点或条件下的测量结果，以确定不同条件对结果变量的影响是否存在统计学上的显著差异。为了确保分析的有效性，需要满足以下假设条件：

在设计的任何区块（block）中都没有显著的异常值。异常值可能会对分析结果产生重大影响，因此需要识别并妥善处理。可以使用rstatix::identify_outliers()函数来查看数据中的离群点。
数据服从正态分布。正态性是方差分析的基本假设之一。可以使用rstatix::shapiro_test()函数来检验数据的正态性。如果数据不服从正态分布，可能需要进行数据转换或采用非参数方法。
方差齐性：不同组之间的差异的方差应该相等。方差齐性检验可以通过rstatix::anova_test()函数进行，该函数会提供方差齐性的检验结果。如果方差不齐，可能需要采用其他方法，如Welch’s ANOVA，来调整分析。
处理水平大于2。重复测量单因素方差分析要求至少有三种不同的处理水平或条件，以便比较它们对结果变量的影响。

输入数据

data("selfesteem", package = "datarium")selfesteem <- selfesteem %>%gather(key = "time", value = "score", t1, t2, t3) %>%convert_as_factor(id, time)head(selfesteem, 3)

#> # A tibble: 3 × 3
#>   id    time  score
#>   <fct> <fct> <dbl>
#> 1 1     t1     4.01
#> 2 2     t1     2.56
#> 3 3     t1     3.24

基本统计特征

selfesteem %>%group_by(time) %>%get_summary_stats(score, type = "mean_sd")

#> # A tibble: 3 × 5
#>   time  variable     n  mean    sd
#>   <fct> <fct>    <dbl> <dbl> <dbl>
#> 1 t1    score       10  3.14 0.552
#> 2 t2    score       10  4.93 0.863
#> 3 t3    score       10  7.64 1.14

可视化

ggboxplot(selfesteem, x = "time", y = "score", add = "point")

在这里插入图片描述

假设评估：离群点

selfesteem %>%group_by(time) %>%identify_outliers(score)

#> # A tibble: 2 × 5
#>   time  id    score is.outlier is.extreme
#>   <fct> <fct> <dbl> <lgl>      <lgl>     
#> 1 t1    6      2.05 TRUE       FALSE     
#> 2 t2    2      6.91 TRUE       FALSE

假设评估：正态分布

selfesteem %>%group_by(time) %>%shapiro_test(score)# ggqqplot(selfesteem, "score", facet.by = "time")

#> # A tibble: 3 × 4
#>   time  variable statistic     p
#>   <fct> <chr>        <dbl> <dbl>
#> 1 t1    score        0.967 0.859
#> 2 t2    score        0.876 0.117
#> 3 t3    score        0.923 0.380

统计检验：ANOVA整体评估变量在所有处理水平的显著性

res.aov <- anova_test(data = selfesteem, dv = score, wid = id, within = time)
get_anova_table(res.aov)

#> ANOVA Table (type III tests)
#> 
#>   Effect DFn DFd      F        p p<.05   ges
#> 1   time   2  18 55.469 2.01e-08     * 0.829

结果：

p-value=2.01e-08是一个极其显著的统计结果，远小于常规的显著性水平（如0.05）。这个结果表明，个人的得分在不同时间点之间存在统计学上的显著差异。换句话说，我们可以非常有信心地拒绝零假设，即不同时间点上的得分没有差异，认为至少在某个时间点上得分与其他时间点存在显著性差异。
广义效应大小（Generalized Effect Size, GES）是一个衡量统计效应大小的指标，它反映了受试者内部因素引起的可变性量。效应大小是独立于样本大小的一个量，它提供了关于观察到的差异或关联实际重要性的额外信息。在许多情况下，即使p值显著，效应大小也可能很小，这表明虽然统计上显著，但实际差异可能并不具有重大意义。因此，GES作为一个补充指标，有助于我们更全面地理解研究结果的实际影响。

统计检验：在完成初步的统计检验，如单因素方差分析（ANOVA），并观察到显著的组间差异（p值小于显著性水平，例如0.05）之后，我们进行了一系列后置检验。这些检验的目的是评估具体组间的两两差异，以确定哪些组对整体显著性贡献最大。

pwc <- selfesteem %>%pairwise_t_test(score ~ time, paired = TRUE,p.adjust.method = "bonferroni")
pwc

#> # A tibble: 3 × 10
#>   .y.   group1 group2    n1    n2 statistic    df          p
#> * <chr> <chr>  <chr>  <int> <int>     <dbl> <dbl>      <dbl>
#> 1 score t1     t2        10    10     -4.97     9    7.72e-4
#> 2 score t1     t3        10    10    -13.2      9    3.34e-7
#> 3 score t2     t3        10    10     -4.87     9    8.86e-4
#> # ℹ 2 more variables: p.adj <dbl>, p.adj.signif <chr>

结果：

任意两组间的p-value均小于显著性水平alpha = 0.05。

可视化：加上显著性标记

pwc_label <- pwc %>% add_xy_position(x = "time")ggboxplot(selfesteem, x = "time", y = "score", add = "point") + stat_pvalue_manual(pwc_label) +labs(subtitle = get_test_label(res.aov, detailed = TRUE),caption = get_pwc_label(pwc_label))

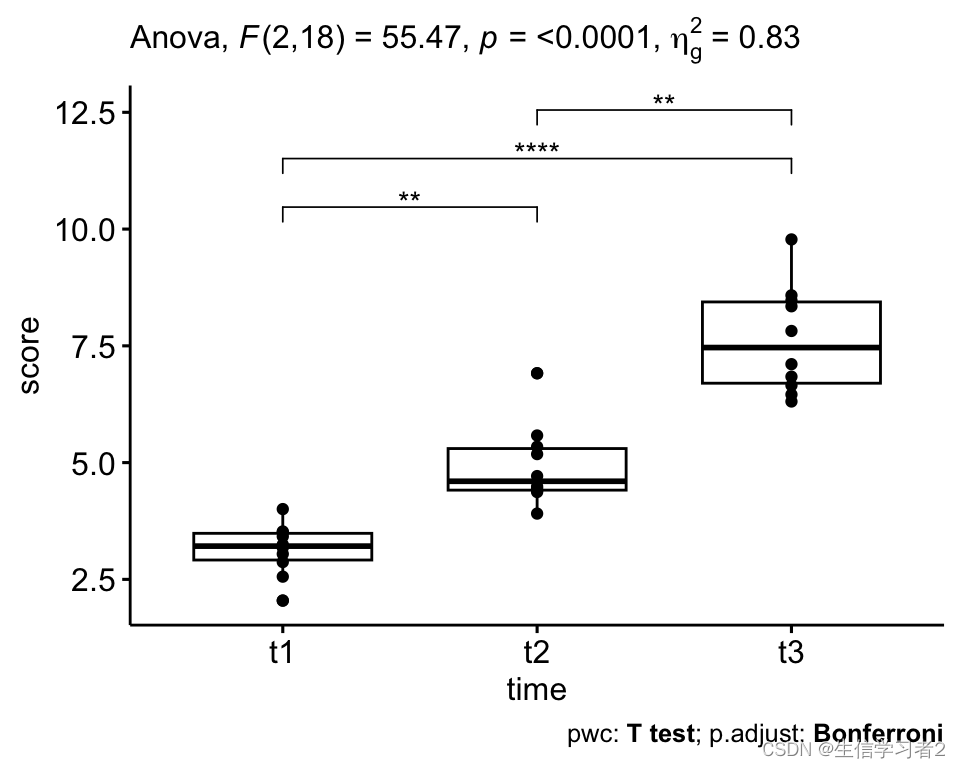
在这里插入图片描述

One-way ANOVA

单因素方差分析（One-Way ANOVA）是一种用于评估一个分类自变量（处理因素）对一个连续因变量影响的统计方法。为了确保分析结果的有效性和可靠性，必须满足以下基本假设条件：

数据服从正态分布。正态性假设意味着每个组的观测值应近似地遵循正态分布的钟形曲线。这可以通过使用rstatix::shapiro_test()函数进行检验来确认。如果数据不满足正态分布，可能需要考虑数据转换或采用非参数的替代方法。
方差齐性。这个假设要求不同组的方差应该相等。如果方差不齐，比较各组均值的差异可能会产生误导。可以通过rstatix::anova_test()函数来检验方差齐性。如果发现方差不齐，可能需要使用Welch’s ANOVA或其他方法来调整分析。
处理水平大于2。单因素方差分析至少需要有三个不同的处理水平或组别，以便比较它们对因变量的影响。如果只有一个或两个处理水平，ANOVA方法将不适用，可能需要使用其他统计方法，如t检验。

数据探索

ggboxplot(PlantGrowth, x = "group", y = "weight",color = "group", palette = c("#00AFBB", "#E7B800", "#FC4E07"),order = c("ctrl", "trt1", "trt2"),ylab = "Weight", xlab = "Treatment")

在这里插入图片描述

检验：评估植物的平均weight是否在三组处理间是显著差异的

res.aov <- aov(weight ~ group, data = PlantGrowth)summary(res.aov)

#>             Df Sum Sq Mean Sq F value Pr(>F)  
#> group        2  3.766  1.8832   4.846 0.0159 *
#> Residuals   27 10.492  0.3886                 
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

结果：根据所得的p值，当p值小于0.05时，我们有足够的证据拒绝零假设，即认为相应的组之间不存在差异。在这种情况下，我们认为组间差异是统计学上显著的，并在报告或表格中用星号（*）来标注这些具有显著性差异的组。

后置检验：组均值之间的多重两两比较 by Tukey HSD (Tukey Honest Significant Differences)

TukeyHSD(res.aov)

#>   Tukey multiple comparisons of means
#>     95% family-wise confidence level
#> 
#> Fit: aov(formula = weight ~ group, data = PlantGrowth)
#> 
#> $group
#>             diff        lwr       upr     p adj
#> trt1-ctrl -0.371 -1.0622161 0.3202161 0.3908711
#> trt2-ctrl  0.494 -0.1972161 1.1852161 0.1979960
#> trt2-trt1  0.865  0.1737839 1.5562161 0.0120064

后置检验2: 采用multcomp::glht方法

The function glht() [in the multcomp package] can be used to do multiple comparison processes for an ANOVA. General linear hypothesis tests are abbreviated as glht.

library(multcomp)summary(glht(res.aov, linfct = mcp(group = "Tukey")))

#> 
#>   Simultaneous Tests for General Linear Hypotheses
#> 
#> Multiple Comparisons of Means: Tukey Contrasts
#> 
#> 
#> Fit: aov(formula = weight ~ group, data = PlantGrowth)
#> 
#> Linear Hypotheses:
#>                  Estimate Std. Error t value Pr(>|t|)  
#> trt1 - ctrl == 0  -0.3710     0.2788  -1.331   0.3909  
#> trt2 - ctrl == 0   0.4940     0.2788   1.772   0.1979  
#> trt2 - trt1 == 0   0.8650     0.2788   3.103   0.0119 *
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> (Adjusted p values reported -- single-step method)

后置检验3: T-test with pairs

pairwise.t.test(PlantGrowth$weight, PlantGrowth$group,p.adjust.method = "BH")

#> 
#>  Pairwise comparisons using t tests with pooled SD 
#> 
#> data:  PlantGrowth$weight and PlantGrowth$group 
#> 
#>      ctrl  trt1 
#> trt1 0.194 -    
#> trt2 0.132 0.013
#> 
#> P value adjustment method: BH

可视化：加上假设检验的结果

pwc_label2 <- PlantGrowth %>%pairwise_t_test(weight ~ group,p.adjust.method = "BH") %>% add_xy_position(x = "group")ggboxplot(PlantGrowth, x = "group", y = "weight", add = "point") + stat_pvalue_manual(pwc_label2) +labs(#subtitle = get_test_label(res.aov, detailed = TRUE),caption = get_pwc_label(pwc_label2))

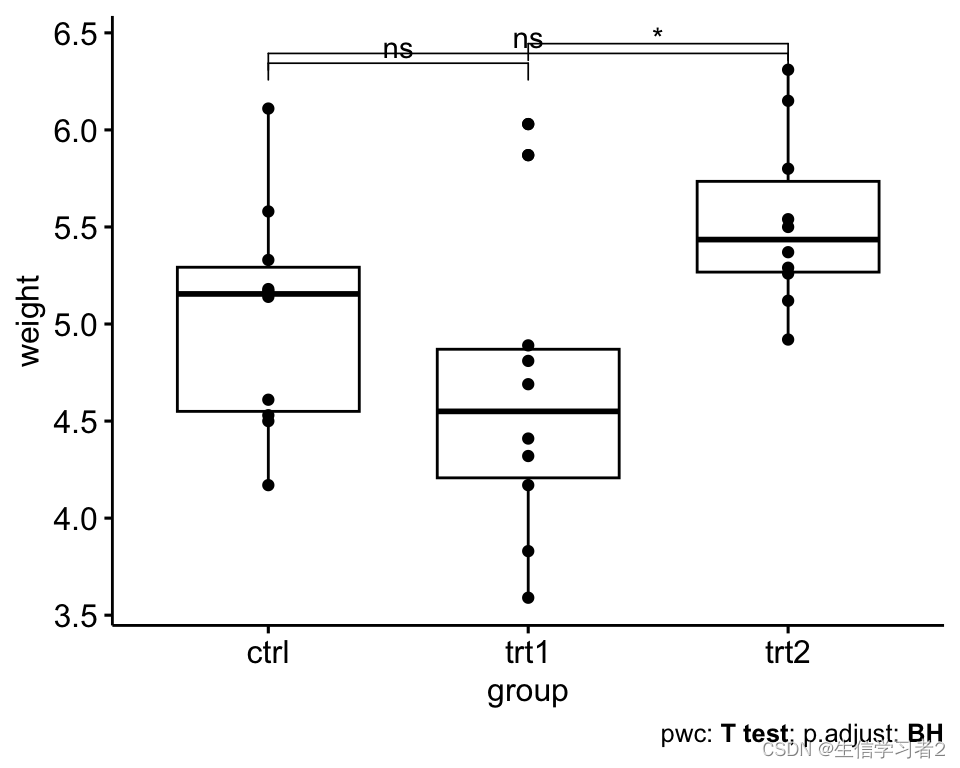
在这里插入图片描述

Friedman test

Friedman检验是一种灵活的非参数检验方法，它不依赖于数据的正态分布假设。这种检验特别适用于以下情况：当数据不满足单向重复测量ANOVA检验所需的正态性条件，或者当因变量是在有序量表上进行测量时。它允许研究者评估多个相关样本之间的差异，而不受数据分布形态的限制。

具体来说，Friedman检验通过计算各组的等级和，然后与理论值进行比较，来确定样本间的等级分布是否存在显著差异。如果检验统计量显著大于理论值，或者相应的p值小于预定的显著性水平（例如0.05），则我们拒绝零假设，认为至少有两个成对组之间存在显著差异。

输入数据

data("selfesteem", package = "datarium")selfesteem <- selfesteem %>%gather(key = "time", value = "score", t1, t2, t3) %>%convert_as_factor(id, time)head(selfesteem, 3)

#> # A tibble: 3 × 3
#>   id    time  score
#>   <fct> <fct> <dbl>
#> 1 1     t1     4.01
#> 2 2     t1     2.56
#> 3 3     t1     3.24

统计检验：friedman test整体评估变量在所有处理水平的显著性

res.fried <- selfesteem %>% friedman_test(score ~ time | id)res.fried# selfesteem %>% friedman_effsize(score ~ time | id)

#> # A tibble: 1 × 6
#>   .y.       n statistic    df        p method       
#> * <chr> <int>     <dbl> <dbl>    <dbl> <chr>        
#> 1 score    10      18.2     2 0.000112 Friedman test# selfesteem %>% friedman_effsize(score ~ time | id)

统计检验：后置检验评估具体组间两两差异结果并做了检验结果校正

pwc <- selfesteem %>%wilcox_test(score ~ time, paired = TRUE,p.adjust.method = "bonferroni")
pwc

#> # A tibble: 3 × 9
#>   .y.   group1 group2    n1    n2 statistic     p p.adj
#> * <chr> <chr>  <chr>  <int> <int>     <dbl> <dbl> <dbl>
#> 1 score t1     t2        10    10         0 0.002 0.006
#> 2 score t1     t3        10    10         0 0.002 0.006
#> 3 score t2     t3        10    10         1 0.004 0.012
#> # ℹ 1 more variable: p.adj.signif <chr>

可视化：加上假设检验的结果

pwc_label <- pwc %>% add_xy_position(x = "time")ggboxplot(selfesteem, x = "time", y = "score", add = "point") + stat_pvalue_manual(pwc_label, hide.ns = TRUE) +labs(subtitle = get_test_label(res.fried, detailed = TRUE),caption = get_pwc_label(pwc_label))

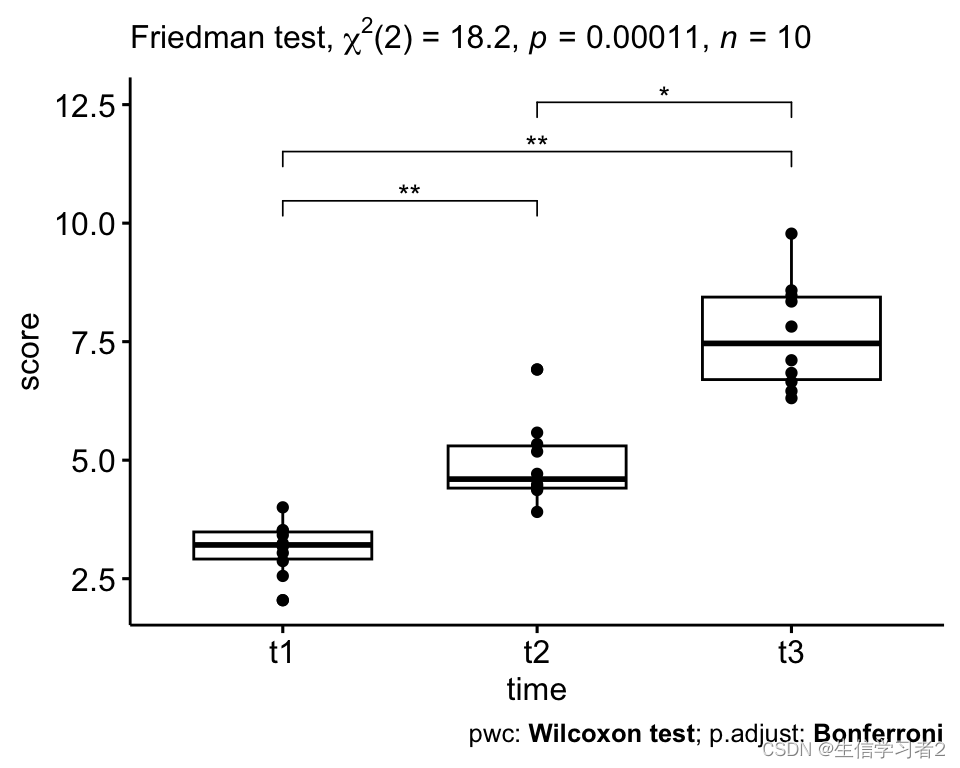
在这里插入图片描述

Kruskal-Wallis test

Kruskal-Wallis检验作为单因素方差分析（ANOVA）的非参数替代方法，在比较两个以上独立组时，提供了一种有效的统计工具。它在本质上扩展了两样本Wilcoxon秩和检验，允许研究者在不依赖数据正态分布假设的情况下，评估多个组的中心趋势是否存在显著差异。

当数据不满足单因素方差分析所需的正态性、方差齐性或独立性假设时，Kruskal-Wallis检验是推荐的分析方法。它通过比较各组的秩和，来确定不同组间是否存在统计学上的显著差异。如果检验统计量显著，即p值小于预定的显著性水平（如0.05），则拒绝零假设，认为至少有两个组之间存在显著差异。

数据探索

PlantGrowth %>% group_by(group) %>%get_summary_stats(weight, type = "common")

#> # A tibble: 3 × 11
#>   group variable     n   min   max median   iqr  mean    sd
#>   <fct> <fct>    <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl> <dbl>
#> 1 ctrl  weight      10  4.17  6.11   5.16 0.743  5.03 0.583
#> 2 trt1  weight      10  3.59  6.03   4.55 0.662  4.66 0.794
#> 3 trt2  weight      10  4.92  6.31   5.44 0.467  5.53 0.443
#> # ℹ 2 more variables: se <dbl>, ci <dbl>

检验：评估植物的平均weight是否在三组处理间是显著差异的

res.kruskal <- PlantGrowth %>% kruskal_test(weight ~ group)res.kruskal# Effect size
# PlantGrowth %>% kruskal_effsize(weight ~ group)

#> # A tibble: 1 × 6
#>   .y.        n statistic    df      p method        
#> * <chr>  <int>     <dbl> <int>  <dbl> <chr>         
#> 1 weight    30      7.99     2 0.0184 Kruskal-Wallis# Effect size
# PlantGrowth %>% kruskal_effsize(weight ~ group)

后置检验：组均值之间的多重两两比较 by Dunn’s test

pwc <- PlantGrowth %>% dunn_test(weight ~ group, p.adjust.method = "bonferroni") 
pwc

#> # A tibble: 3 × 9
#>   .y.    group1 group2    n1    n2 statistic       p  p.adj
#> * <chr>  <chr>  <chr>  <int> <int>     <dbl>   <dbl>  <dbl>
#> 1 weight ctrl   trt1      10    10     -1.12 0.264   0.791 
#> 2 weight ctrl   trt2      10    10      1.69 0.0912  0.273 
#> 3 weight trt1   trt2      10    10      2.81 0.00500 0.0150
#> # ℹ 1 more variable: p.adj.signif <chr>

后置检验2: 采用wilcox_test方法

pwc2 <- PlantGrowth %>% wilcox_test(weight ~ group, p.adjust.method = "bonferroni")
pwc2

#> # A tibble: 3 × 9
#>   .y.    group1 group2    n1    n2 statistic     p p.adj
#> * <chr>  <chr>  <chr>  <int> <int>     <dbl> <dbl> <dbl>
#> 1 weight ctrl   trt1      10    10      67.5 0.199 0.597
#> 2 weight ctrl   trt2      10    10      25   0.063 0.189
#> 3 weight trt1   trt2      10    10      16   0.009 0.027
#> # ℹ 1 more variable: p.adj.signif <chr>

可视化：加上假设检验的结果

pwc_label2 <- pwc %>% add_xy_position(x = "group")ggboxplot(PlantGrowth, x = "group", y = "weight", add = "point") + stat_pvalue_manual(pwc_label2, hide.ns = TRUE) +labs(subtitle = get_test_label(res.kruskal, detailed = TRUE),caption = get_pwc_label(pwc_label2))

在这里插入图片描述

Blocked Wilcoxon rank-sum test

**Two-sided Wilcoxon tests blocked for ‘study’**是一种统计检验方法，它专门设计用于在多个研究中评估数据的差异性，同时考虑不同研究来源的潜在影响。与传统的在每个研究内部独立进行Wilcoxon检验的方法不同，这种检验通过’blocking’或’stratifying’的方式，对来自不同研究的数据进行分组处理。

通过这种分层的Wilcoxon检验，我们可以更准确地控制和调整不同研究之间的变异性，从而减少这些变异性对整体分析结果的影响。这种检验方法不仅考虑了每个研究内部的数据分布，而且还评估了跨研究的总体趋势和模式。

进行Two-sided Wilcoxon tests时，检验的双侧性（two-sided）意味着我们关注的是两个方向上的差异，即比较的两组之间的差异可能是正向的也可能是负向的。这种双侧检验为我们提供了更全面的视角，以评估不同研究中观察到的效应大小和方向。

formula: a formula of the form y ~ x | block where y is a numeric variable, x is a factor and block is an optional factor for stratification.

# 安装并加载coin包
library(coin)# 示例数据，确保group和study列均为因子类型
data <- data.frame(variable = rnorm(100),group = factor(rep(c("A", "B"), 50)),study = factor(rep(c("Study1", "Study2"), each = 50))
)# 使用wilcox_test进行分组Wilcoxon检验
result <- coin::wilcox_test(variable ~ group | study, data = data)
print(result)

#> 
#>  Asymptotic Wilcoxon-Mann-Whitney Test
#> 
#> data:  variable by
#>   group (A, B) 
#>   stratified by study
#> Z = 0.50757, p-value = 0.6118
#> alternative hypothesis: true mu is not equal to 0

总结

对于两组数据的比较，我们可以选择t-test或Wilcoxon检验。如果数据满足正态分布的假设，t-test是一个合适的选择，因为它是参数检验方法，基于数据的正态分布特性。对于不符合正态分布的数据，我们推荐使用Wilcoxon检验，这是一种非参数检验方法，不依赖于数据的分布形态。
当比较三组或更多组的数据时，如果数据满足正态分布和方差齐性的假设，我们可以使用ANOVA（方差分析）来评估组间差异。然而，对于不满足这些假设的情况，Friedman检验或Kruskal-Wallis（KW）检验提供了非参数的替代方法，允许我们在不依赖数据分布特性的情况下进行组间比较。
对于三组数据的初步检验，如果结果显示组间存在显著差异，我们通常需要进行后置检验来解析具体的组间差异。后置检验可以帮助我们识别哪些特定的组对之间的差异是统计学上显著的，从而提供更深入的分析结果。
在进行假设检验之前，数据探索是一个重要的步骤。这包括对数据的正态性进行评估，例如使用Shapiro-Wilk检验等方法，以及通过箱线图来评估组间的分布情况。这些探索性分析有助于我们了解数据的特性，为选择合适的统计检验方法提供依据，并确保后续分析的准确性。

这篇关于数据分析：假设检验方法汇总及R代码实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！