本文主要是介绍R假设检验之Breusch-Godfrey检验(Breusch-Godfrey Test),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
R假设检验之Breusch-Godfrey检验(Breusch-Godfrey Test)

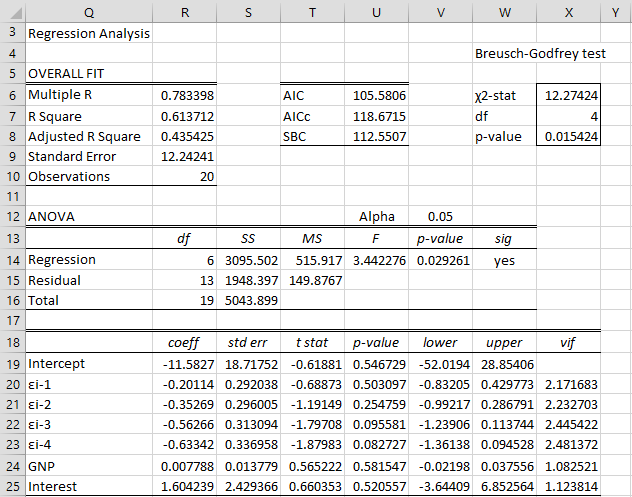
线性回归中的一个关键假设是残差之间不存在相关性,即残差是独立的。
为了测试一阶自相关,我们可以执行Durbin-Watson检验。然而,如果我们想测试高阶的自相关(autocorrelation),那么我们需要执行一个Breusch-Godfrey检验。
Breusch-Godfrey检验使用以下假设:
H0(零假设):小于或等于p的任何阶都不存在自相关。
Ha(替代假设):在小于或等于p的某个阶上存在自相关。
检验统计量服从p个自由度的卡方分布。
如果这个检验统计量对应的p值小于一定的显著性水平(如0.05),那么我们可以拒绝零假设,并得出小于或等于p的某个阶的残差之间存在自相关的结论。
为了在R中执行Breusch-Godfrey测试,我们可以使用lmtest库中的bgtest(y~x,order=p)函数。
我们创建一个包含两个预测变量(x1和x2)和一个响应变量(y)的仿真数据集。
#create dataset
df <- data.frame(x1=c这篇关于R假设检验之Breusch-Godfrey检验(Breusch-Godfrey Test)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






![[UVM]6.component driver monitor sequencer agent scoreboard env test](https://i-blog.csdnimg.cn/direct/d6155f8e9cb5494582087a4fa47916e2.png)