本文主要是介绍假设检验|第三章:统计学中的显著性水平α和P,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章来自微信公众号:发现Minitab
概述
在假设检验中,我们很多时候对显著性水平α和P值理解不透彻?在这篇文章中,我将继续关注概念和图形,以帮助您更直观地理解假设检验在统计学中的工作原理。
为了实现它,我将在我之前文章的基础上将显著性水平α和P值添加到图形中,以便执行单样本t检验。当您可以看到真正意义上的统计意义时,您会更容易理解!
在上一篇文章中我们想确定我们的样本平均值(330.6)是否表明今年的平均能源成本与去年260美元的平均能源成本显著不同。


上面的概率分布图显示了我们在原假设为真(样本均值= 260)的情况下获得的样本均值分布。在这个概率分布图上,我们应该在哪里绘制图表上的统计显著性线呢?现在我们将添加显著性水平α和P值,这是我们需要的决策工具。
我们将使用这些工具来检验以下假设:
- 原假设:总体均值等于假设均值(260)。
- 备择假设:总体均值与假设均值不同(260)。
一、什么是显著性水平α ?
显著性水平α,是在原假设为真时拒绝原假设的概率。例如,显著性水平0.05表示当没有实际差异时得出存在差异,会有5%的风险。
由于其技术性质,这些类型的定义很难理解,但图形使概念更容易理解。
显著性水平α在图形上围成的面积为拒绝域,它决定了我们将在图上绘制的拒绝域临界值。

在上图中,两个阴影区域与原假设值260等距,每个区域的概率为0.025,总共为0.05。在统计中,我们将这些阴影区域称为双尾检验的拒绝域。图中显示我们的样本均值(330.6)落在拒绝域,这表明总体均值显著不等于假设均值260。
我们还可以使用0.01的其他常见显著性水平来判断它是否具有统计学意义。
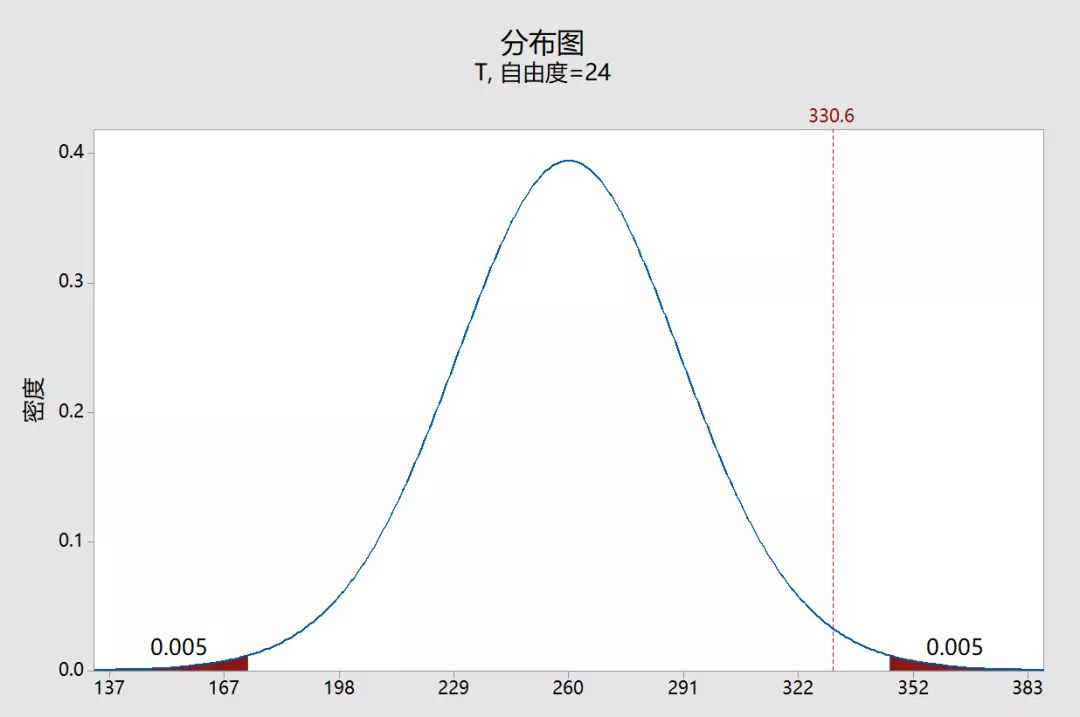
两个阴影区域的概率均为0.005,总概率为0.01。这次我们的样本均值不落在拒绝域,我们不能拒绝原假设。此比较显示了在开始分析之前需要选择显著性水平的原因。
使用该图,我们不用P值也能够确定我们的结果在0.05水平上具有统计显著性。但是,当您使用统计软件生成的数字输出时,您需要将P值与您的显著性水平进行比较以进行此确定。
二、什么是P值 ?
P值是一概率值,指的是当原假设H0成立时,出现目前情况的概率(严格说是:当原假设H0成立时,出现目前状况或对原假设更不利状况,即对备择假设更有利状况的概率)。
P值的定义虽然在技术上是正确的,但有点复杂,用图表更容易理解!为了绘制我们的示例数据集的P值,我们需要确定样本均值和原假设值之间的距离(330.6-260 = 70.6)。接下来,我们可以绘制获得样本均值的概率,该均值在分布的两个尾部中至少是极端的(260 +/- 70.6)。
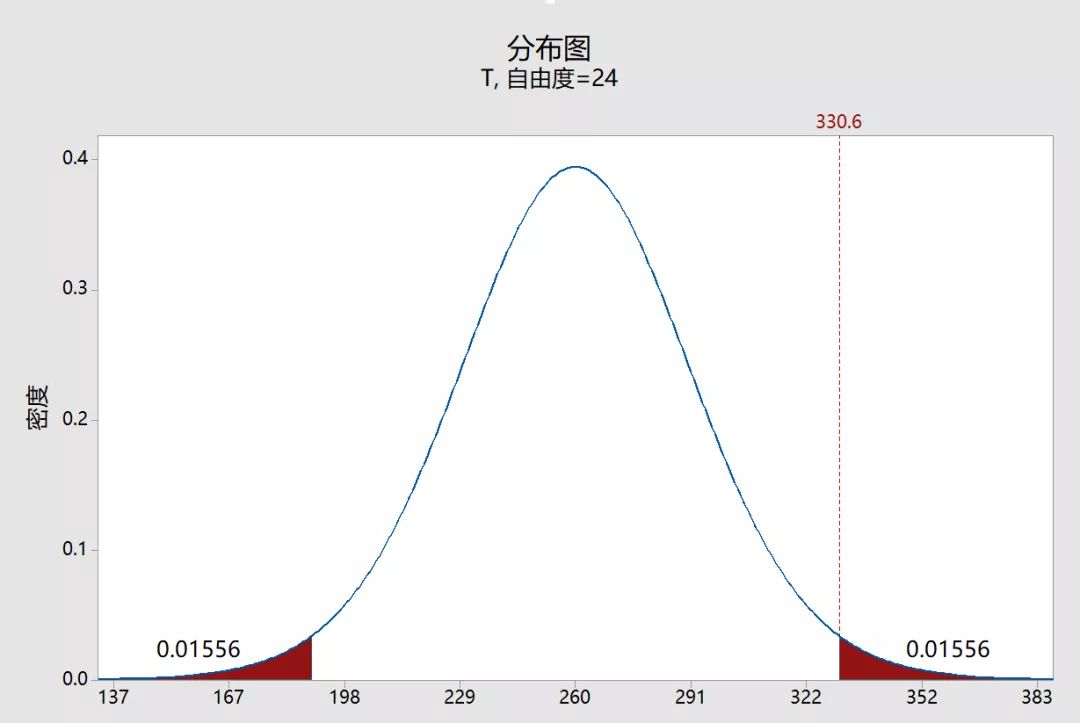
在上图中,两个阴影区域的概率均为0.01556,总概率为0.03112。如果总体均值为260,则该概率表示获得样本均值的可能性至少与分布尾部中的样本均值一样极端。这是我们的P值!
当P值小于或等于显著性水平时,则拒绝原假设。如果我们将P值作为示例并将其与常用显著性水平进行比较,则它与先前的图形结果相匹配。P值0.03112在α水平为0.05时具有统计学显著性,但在0.01水平时不具有统计学意义。如果我们坚持0.05的显著性水平,我们可以得出结论,人口的平均能源成本大于260。
对于P值的解释,一个常见的错误是将P值解释为原假设为真的概率,要理解为什么这种解释不正确,我将在后续文章中介绍。
三、关于统计显著性结果的讨论
假设检验评估关于总体的两个相互排斥的陈述,以确定样本数据最佳支持哪个陈述。当样本统计量相对于原假设足够不寻常时,检验结果具有统计学意义,即我们可以拒绝整个群体的原假设。假设检验中的“不寻常”定义为:
- 原假设H0 - 图表以原假设值为中心。
- 显著性水平α - 确定拒绝域的临界值。
- 我们的样本统计数据是否落在拒绝域?
请记住,没有神奇的显著性性水平可以区分具有真实效果的研究和100%不具有准确性的研究。常见的alpha值0.05和0.01仅仅基于传统。对于0.05的显著性水平,期望在原假设为真时的 5%的拒绝域中获得样本平均值。在这些情况下,您不会知道原假设是正确的,但您会拒绝它,因为样本均值落在拒绝域。
这篇关于假设检验|第三章:统计学中的显著性水平α和P的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






