本文主要是介绍python统计分析——统计学假设检验和统计学建模,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
参考资料:python统计分析【托马斯】
对于大部分统计问题,我们可以从两个角度来看:可以做一个假设,并证实或证伪;或是建立一个统计模型,并分析模型参数的显著性。我们用经典的t检验做例子进行介绍:
1、t检验
假设我们在两种不同场景下对一个赛车对的表现进行衡量。代码如下:
# 导入库
import numpy as np
from scipy import stats# 设置随机种子,用于复现结果
np.random.seed(123)
# 生成第一次比赛的数据
race_1=np.round(np.random.randn(20)*10+90)
# 生成第二次比赛的数据
race_2=np.round(np.random.randn(20)*10+85)
# 进行配对t检验
t,pVal=stats.ttest_rel(race_1,race_2)
# 输出结果:
print("两次比赛结果相等的概率是:{0:5.3f}".format(pVal))
2、统计学建模
用统计学模型的角度来表达,我们假设第一次和第二次的比赛差异是一个常量(本例的无效假设是该常量等于0)。这个模型只有一个参数:这个常量。我们可以用下面的代码得到这个参数以及它的置信区间和大量其他信息。
# 导入新的库
import pandas as pd
import statsmodels.formula.api as smf# 将数据生成dataframe格式
df=pd.DataFrame({'Race1':race_1,"Race2":race_2
})# 用普通最小二乘法拟合统计模型
result=smf.ols(formula='I(Race2-Race1)~1',data=df).fit()
# 输出拟合结果
print(result.summary())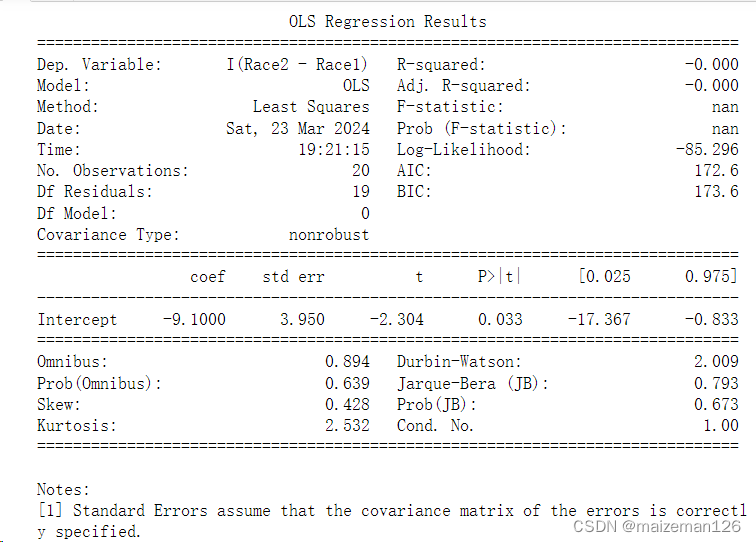
最重要的是拟合的步骤。来自statsmodels的smf.ols函数能够检验模型,该模型描述了第一次和第二次比赛之间的而差异,并且只有一个偏差,这个偏差在建模型语句中叫作截距。上图的结果显示截距为0 的概率只有0.033,和0的差异显著。
这里重点说明的是:用统计学模型得到的截距t值和p值与传统的t检验得到的结果是一样的。
这篇关于python统计分析——统计学假设检验和统计学建模的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






