本文主要是介绍常见分布与假设检验,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、随机变量的两种类型
根据随机变量可能取值的个数分为离散型(取值有限)和连续型(取值无限)两类。
1.1 离散型随机变量
对于离散型随机变量,使用概率质量函数(probability mass function),简称PMl,来描述其分布律。
常用的离散型随机分布:二项分布,泊松分布
1.2 连续型随机变量
对于连续型随机变量,使用概率密度函数(probability density function),简称PDF,来描述其分布情况。
连续型随机变量的特点在于取任何固定值的概率都为0,因此讨论其在特定值上的概率是没有意义的,应当讨论其在某一个区间范
围内的概率,这就用到了概率密度函数的概念。
常用的连续型随机分布:均匀分布,正态分布,指数分布
1.3 常用分布

1.4 常见分布的均值和方差汇总
离散型分布

连续型分布

1.5 Python代码实战
二、假设检验
基本概念:假设检验问题时统计推断中的一类重要问题,在总体的分布函数完全未知或只知其形式,不知其参数的情况,为了推断总体的某些未知特性,提出某些关于总体的假设,这类问题被称为假设检验。
基本步骤与统计量的选择
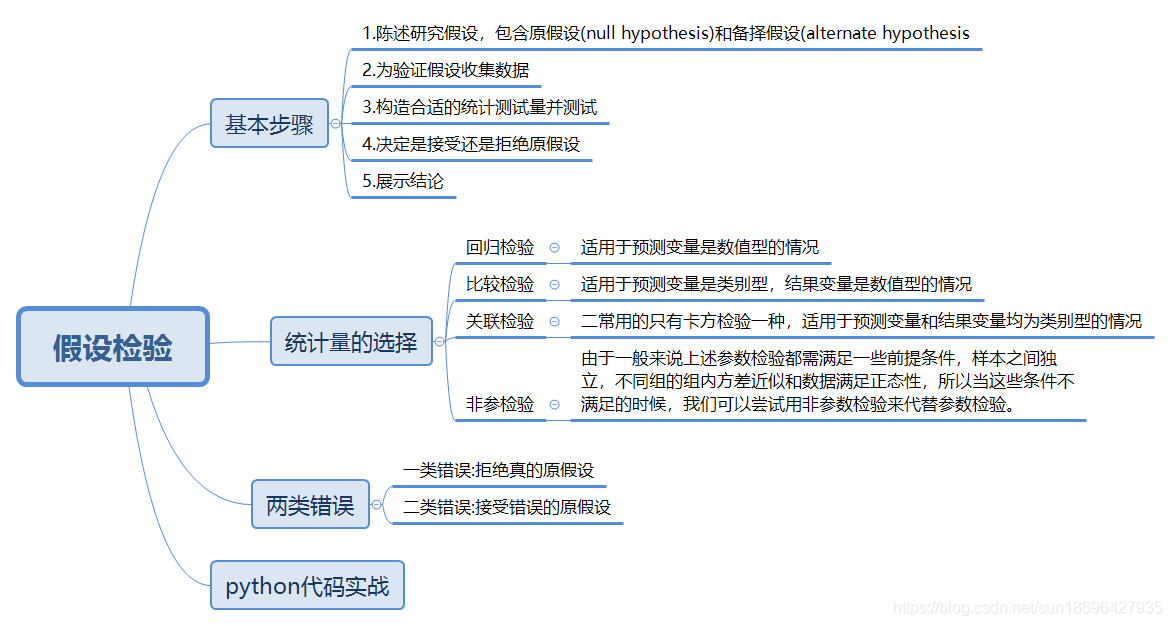
假设检验中常见问题
1、为什么犯α错误与犯β错误的机会是此消彼长的呢?
α错误是原假设是对的但我们拒绝掉的错误,即弃真错误;
β错误是原假设是错的但我们接受的错误,即取伪错误;
当我们想要犯α错误的机会变小的时候,也就是更有可能认同原假设是对的;但这就容易导致原假设本身其实是错的,我们却更有可能接受而犯β错误。我们需要注意的是原假设是正确还是错误的客观事实是没有任何变化的,我们的统计推断行为只是尽可能的让我们得出的结论更加接近真相。由于原假设往往更明确,我们通常倾向于缩小犯a错误的机会。
2、P值与拒绝阈决策的区别
P值是原假设成立的概率值,P值如果大于所给出的显著性水平(一般大于0.5)的话,则不能拒绝原假设;如果小于显著性水平的话,则拒绝原假设
3、当统计检验不显著时,是否只能说此时不拒绝原假设而不能说接受原假设?
具体可参考以下链接,简单说来就是,之所以要说不拒绝原假设而不直接说接受原假设是因为我们不拒绝原假设不一定原假设就是对的,只是我们在当前的数据支撑下没有能找到推翻原假设的证据,也就是说我们还有可能犯第二类错误。所以,说不拒绝原假设是为了表述的科学严谨性
https://www.zhihu.com/question/24820124?sort=created
这篇关于常见分布与假设检验的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


