aic值检验 p值_参数估计和假设检验

前言：所谓统计推断，就是利用样本所提供的信息对总体的某些统计特征进行估计或者判断，进而认识总体。统计推断分为两大类：参数估计，假设检验。

1 .参数估计

参数估计和假设检验是统计推断的基本内容，几乎所有统计建模的PROC步都会设计参数估计以及相对应的假设检验。假设总体

的分布函数的类型已知，但其中一个或者多个参数未知，那么就需要对这些未知的参数做出合理的估计，并且对估计做出评价，这就是

参数估计分为 点估计和区间估计。

1.1 点估计

也称为定值估计。以一个单一的取值，去近似的作为未知的参数的估计值。

例如样本的均值

可以用来估计总体的均值

，样本的标准差

可以用来估计总体的标准差

。

点估计的方法：

矩估计法，最小二乘法，极大似然法

1.2 区间估计

对于未知参数

，我们除了关注点估计

外，还希望估计出一个范围，并希望知道参数

落在这个范围的可信程度，这就是区间估计。这样的区间即参数的置信区间。

1.2.1 置信区间

就是一个包含统计量值的取值范围，并且这个范围在一定的置信水平下包含参数

的真实值。

数学表达为：

若有一分布

,

为未知参数，对于给定值

，若由样本计算出两个统计量

和

,满足

,则随机区间

是

置信水平为

的置信区间，

是置信水平，

是显著性水平，

和

为置信上下限。

例如，95%置信区间：从总体中重复抽取100个相同样本容量的样本，并且计算了100个置信区间，那么这100个置信区间有95个包含了总体的均值。

我们都希望提高置信水平，但是在样本容量一定的情况下，提高置信水平，势必会使置信区间变宽，估计的精度降低。

1.2.2 均值的置信区间

均值标准误差：

刻画样本均值对于总体均值的变异程度。

例子：计算sashelp.fish的bream的95%置信区间。

proc means data=sashelp.fish mean std stderr clm maxdec=2 n;
where species="Bream";
var height;
title "95% confidence interval for bream";
run;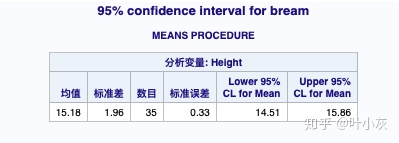

• stderr：计算标准误差值
• clm：计算均值的置信区间
• 添加 alpha=选项可以计算不同置信水平的置信区间。

本个案例中，可以认为区间（14.51，15.86）包含总体均值的可能性为95%，区间的宽度很窄，可以认为样本均值是总体均值的一个比较准确的估计。

2.假设检验

在总体的分布函数只知其形式，但不知其参数的情况下，或者对总体分布完全未知的情况下，为了推断总体的某些未知特征，现提出某些关于总体的假设，然后根据样本采用适当的方法，对所提出的假设作出接受或拒绝的决策，这一过程就是假设检验。

2.1 基本原理

例子：假如我手上有一枚硬币，一般的硬币都是均匀的，如果我认为它是不均匀的，我就必须给出足够的理由来证明。为此我制定了一个原则：连续抛掷5次，5次都朝上或者朝下，则认为该硬币不均匀，否则&#x