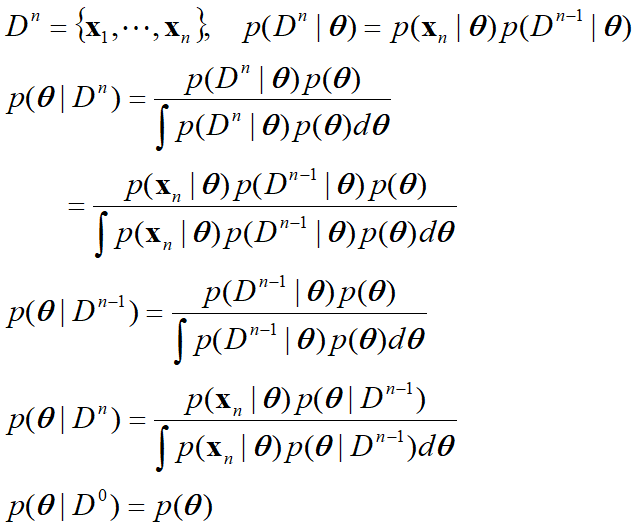参数估计专题
(未完待续)概率论之参数估计
两个独立正态总体的均值比较 情况一: 例子 情况二: 情况三: 两个非正态分布总体的均值比较 例子: 两个总体比例比较 例子: 两个独立正态总体的方差比较 估计量与估计值 对于已知类型的分布,估计分布函数参数是关键 无偏性 有效性 相合性 矩阵计法 均匀分布的矩估计量 正态分布的矩估计量
python数据分析--- ch12-13 python参数估计与假设检验
python数据分析--- ch12-13 python参数估计与假设检验 1. Ch12--python 参数估计1.1 参数估计与置信区间的含义及函数版1.1.1 参数估计与置信区间的含义1.1.2 参数估计函数版1.1.3 参数估计函数版 1.2 Python单正态总体均值区间估计1.2.1 方差 σ 2 \sigma^2 σ2已知1.2.2 方差 σ 2 \sigma^2 σ2未知
贝叶斯参数估计vs贝叶斯学习
贝叶斯参数估计和贝叶斯学习都依赖于贝叶斯定理,都强调先验概率在推断过程中的重要性,并都使用后验概率进行参数估计或总体分布的推断。 贝叶斯参数估计更侧重于如何利用贝叶斯定理进行具体的参数估计,使总期望风险最小;而贝叶斯学习更侧重于如何利用贝叶斯定理和先验信息进行总体的学习和推理过程。 贝叶斯参数估计 定义:贝叶斯参数估计是一种参数估计方法,它利用贝叶斯定理结合新的证据(观测数据)及以前的先验概率
【计算机视觉】Lecture 14:参数估计
总结:变换 参数估计 我们将会讨论以下方面的参数估计: 几何模型(如直线、平面、曲面)几何变换(我们讨论过的任何参数化变换) 最小二乘法是解决这两个问题的通用策略! 参数估计:拟合几何模型 总体思路: 希望使模型适合原始图像特征(数据):特征可以是点,边缘,甚至区域参数化模型:模型例子是Rn的一个元素,也就是模型实例 = (a1, a2,…,an)定义一个误差函数E(模型i,数据
MATLAB中对自定义函数进行参数估计的方法
先输入x和y的数据。然后在matlab的工作栏输入cftool.在弹出来的拟合工具箱内选择变量为你的x和y.然后右边的拟合方法选择custom equation,然后输入你要拟合的式子的形式,按fit就可以拟合了。
[闲聊统计]之参数估计是什么?(上)
参数估计是推断统计的重要内容之一。它是在抽样及抽样分布的基础上,根据样本统计量来推断所关心的总体参数。说白了,就是用样本信息来代替总体信息 例如:现在要调查某大学大学生的一个消费情况,假设全校大学生的平均消费金额为 μ \mu μ,那么我们随机抽取一个样本,这个样本的平均消费水平为 x ‾ \overline{x} x,理论上,可以用 x ‾ \overline{x} x代替 μ \mu
(八)目标跟踪中参数估计(似然、贝叶斯估计)理论知识
目录 前言 一、统计学基础知识 (一)随机变量 (二)全概率公式 (三)高斯分布及其性质 二、似然是什么? (一)概率和似然 (二)极大似然估计 三、贝叶斯估计 (一)古典统计学与贝叶斯统计学的区别 (二)贝叶斯公式 总结 前言 目标跟踪过程可以看做参数估计的过程,即利用测量信息实时对目标状态进行估计,需要用到很多概率统计的基础知识。在此针对参数估计
【概率论】期末复习笔记:参数估计
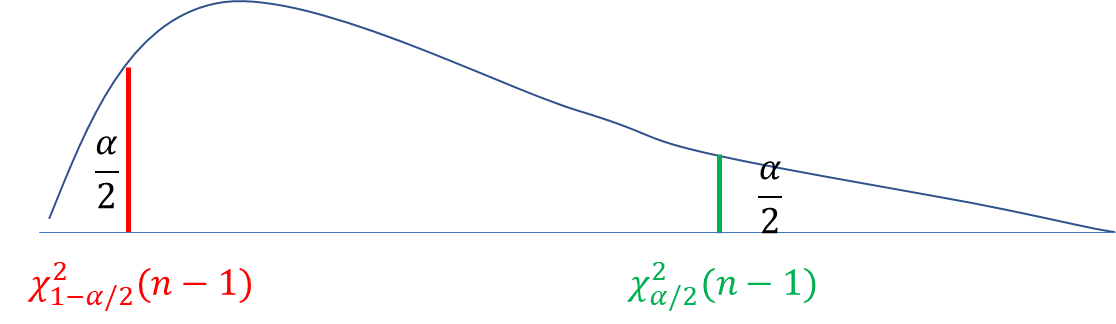
参数估计目录 一、点估计1. 估计量的概念2. 估计量的求法矩估计法最大似然估计法 二、估计量的评选标准1. 无偏性2. 有效性3. 相合性总结 三、区间估计1. 双侧区间估计2. 单侧区间估计 四、正态总体参数的区间估计 σ 2 已知,考察 μ \color{dodgerblue}\sigma^2\text{已知,考察}\mu σ2已知,考察μ σ 2 未知,考察 μ \color{do
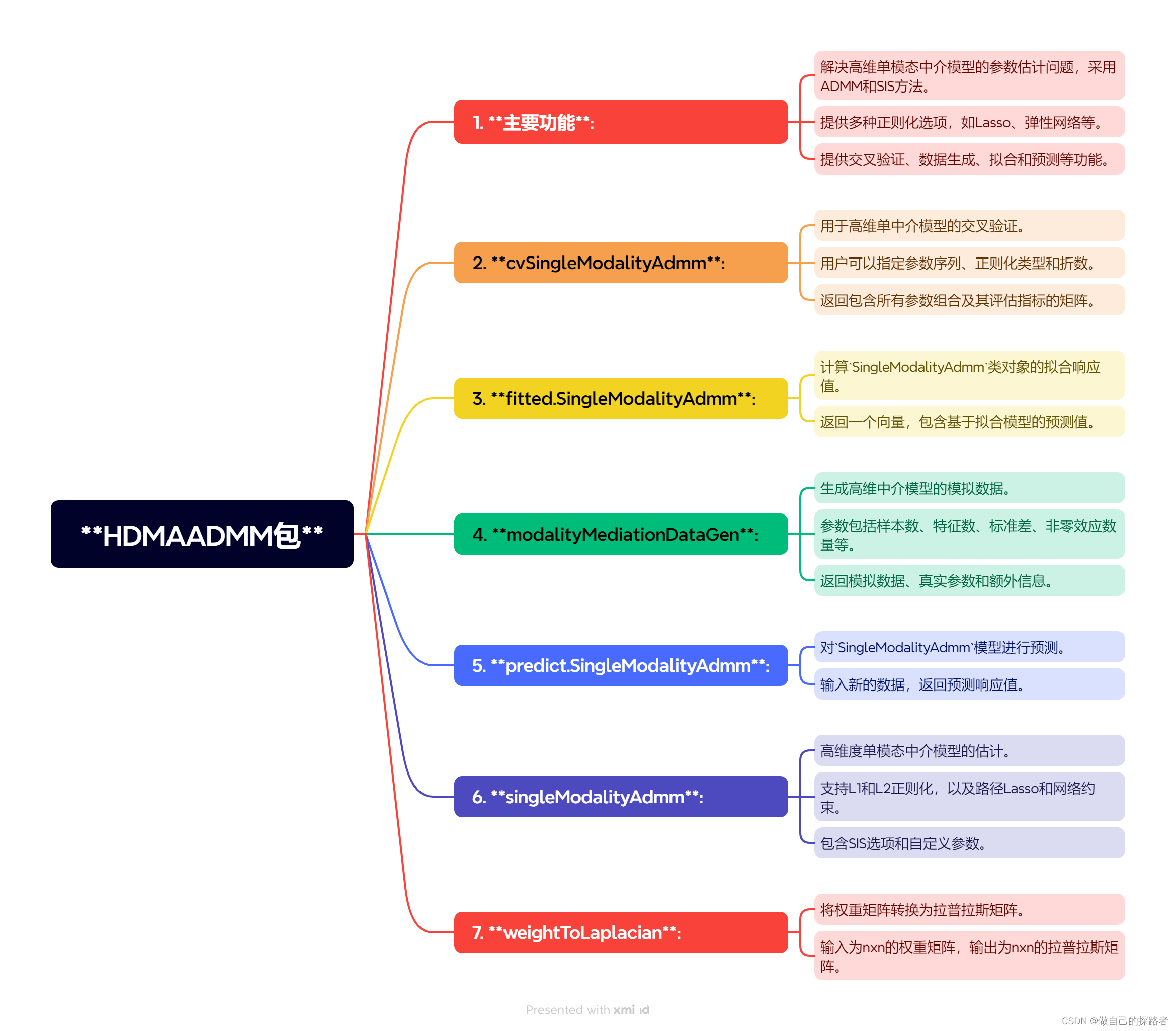
高维中介数据:基于交替方向乘子法(ADMM)的高维度单模态中介模型的参数估计(入门+实操)
全文摘要 用于高维度单模态中介模型的参数估计,采用交替方向乘子法(ADMM)进行计算。该包提供了确切独立筛选(SIS)功能来提高中介效应的敏感性和特异性,并支持Lasso、弹性网络、路径Lasso和网络约束惩罚等不同正则化方法。 Pathway Lasso 背景 传统的结构方程建模(SEM)在处理大量中介变量时变得不稳定且计算复杂。Pathway Lasso引入了一个新的惩罚函数,它是一
现代信号处理学习笔记(二)参数估计理论
参数估计理论为我们提供了一套系统性的工具和方法,使我们能够从样本数据中推断总体参数,并评估估计的准确性和可靠性。这些概念在统计学和数据分析中起着关键的作用。 目录 前言 一、估计子的性能 1、无偏估计与渐近无偏估计 2、估计子的有效性 两个无偏估计子的比较 无偏与渐近无偏估计子之间的比较 二、Fisher信息与Cramer-Rao不等式 1、Fisher信息 2、Cr
时间序列分析 - ARMA/ARIMA参数估计及模型预测
整体处理流程如下: 【平稳化处理】 根据ADF单位根检验看序列是否平稳,对于非平稳序列可以进行差分,对数等等。 对于得到的平稳序列需要检测是否为白噪声,如果是就没有必要再分析了。 【白噪声检验】 1)由于白噪声序列期望为0,方差固定。因此会在y=0上下小幅波动,比如: 2
Python统计分析——参数估计
参考资料:用python动手学统计学 所谓参数就是总体分布的参数。 1、导入库 # 导入用于数值计算的库import numpy as npimport pandas as pdimport scipy as spfrom scipy import stats# 导入用于绘图的库from matplotlib import pyplot as pltimport
参数估计 评价估计量的标准
目录 https://blog.csdn.net/weixin_45792450/article/details/109314584 无偏性 我们希望估计量 θ ^ \hat \theta θ^的取值不要偏高也不要偏低,即 θ ^ \hat \theta θ^的平均取值与 θ \theta θ的真值一致,于是导出了无偏性标准: 定义 设 θ ^ = θ ^ ( X 1 , X 2 ,
非参数估计法之 parzen窗方法和k近邻方法估计概率密度
无论是参数估计还是费参数估计 其目的都是为了求出总体的概率密度函数 parzen窗 基本原理 嗯哼哼 ,画个圈圈 ,在圈圈里面又画一个正方形,在往圈圈里面随机扔豆豆,豆豆在正方形里面的概率约等于在正方形内的总数k比豆豆总数n即k/n,其正好是正方形与圈圈的面积比,假设正方形的面积为R 设豆豆落在正方形里面的概率为P = k/n,假设豆豆落在正方形的每一个点上的概率一样,则落在正方形中的任意
aic值检验 p值_参数估计和假设检验
前言:所谓统计推断,就是利用样本所提供的信息对总体的某些统计特征进行估计或者判断,进而认识总体。统计推断分为两大类:参数估计,假设检验。 1 .参数估计 参数估计和假设检验是统计推断的基本内容,几乎所有统计建模的PROC步都会设计参数估计以及相对应的假设检验。假设总体 的分布函数的类型已知,但其中一个或者多个参数未知,那么就需要对这些未知的参数做出合理的估计,并且对估计做出评价,这
【图解例说机器学习】参数估计 (MLE and MAP)
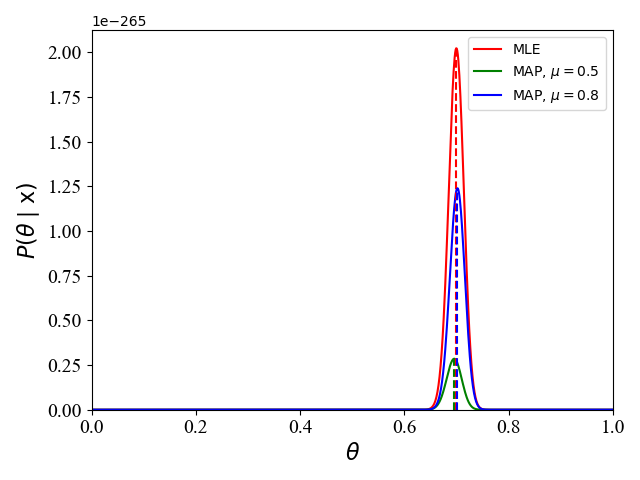
参数估计:给定一个数据集,我们希望用一个给定的分布去拟合该数据集的分布,确定该分布的参数的过程就是参数估计。例如,我们用二项分布去拟合多次投掷硬币的情况,计算该二项分布的最优参数(出现正面的概率 θ \theta θ)就是参数估计。 下面,我们介绍在机器学习中常用的参数估计:极大似然估计 (Maximum Likelihood Estimation, MLE),最大后验概率估计 (Maximu
机器学习练习记录(3):HMM中,如果已知观察序列和产生观察序列的状态序列,如何直接进行参数估计?
在HMM中,如果已知观察序列和产生观察序列的状态序列,那么可用以下哪种方法直接进行参数估计() A.EM算法 B.维特比算法 C.前向后向算法 D.极大似然估计 EM算法: 只有观测序列,无状态序列时来学习模型参数,即Baum-Welch算法 维特比算法: 用动态规划解决HMM的预测问题,不是参数估计 前向后向:用来算概率 极大似然估计:即观测序列和相应的状态序列都存在时的监督学习算法
多平面包络的圆柱体参数估计
多平面包络的圆柱体参数估计 场景 现有多个空间平面包络一个柱体,从圆柱顶端俯视如图所示: 中心位置为圆柱实际所在位置。现在已知这些平面的参数(每个平面的方程均为ax+by+cz+d=0形式, 参数为a,b,c,d),希望求解它们包络的这个圆柱的几何信息。 分析 三维空间中,圆柱的几何信息有两类表达方式: 圆柱中轴的方向向量 ( u , v , 1 ) (u,v,1) (u,v,1)和中
参数估计中字母顶上的符号的含义
hat均值,估计值,用于表示这个量是随机变量的均值而不是随机变量bar tilde误差值,测量值 什么都不加是真值dot导数 Innovation: 时间序列估计中的误差
【梅西迭代姊妹篇2】BCH码和m序列参数估计(梅西迭代算法求多项式的C语言实现)
伯利坎普迭代算法解决了BCH码译码中求错位多项式 σ ( x ) \sigma (x) σ(x)的问题,即用迭代算法求解方程组,极大地加快了译码速度。求最短线性移存器的迭代算法是梅西(J.Massey)于1969年提出的,而且指出了与BCH码迭代译码算法之间的关系,即求最短线性移存器的迭代算法实质上是伯利坎普提出的BCH码译码的迭代算法。 运行效果
数理统计基础:参数估计与假设检验
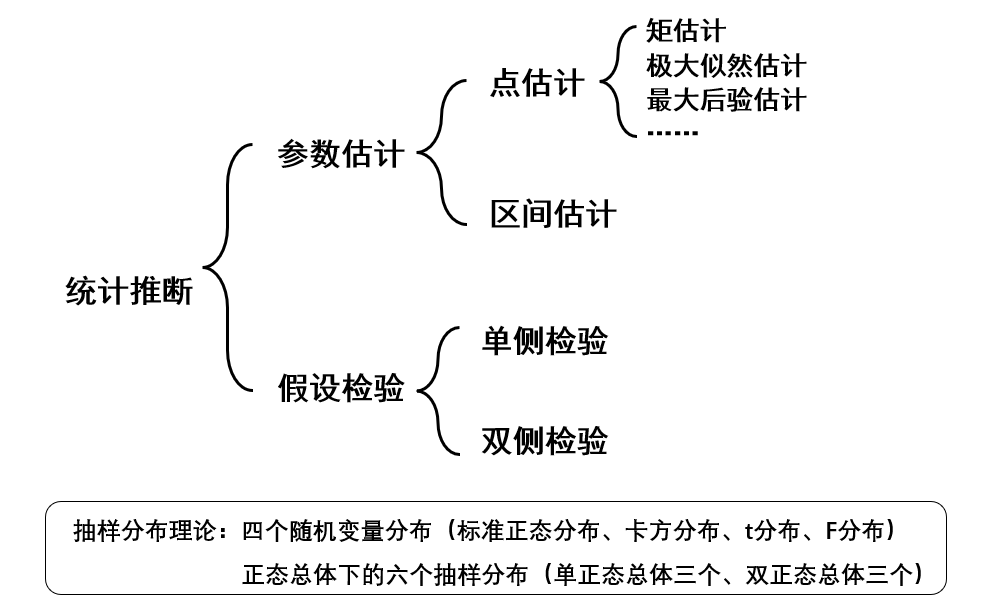
在学习机器学习的过程中,我充分感受到概率与统计知识的重要性,熟悉相关概念思想对理解各种人工智能算法非常有意义,从而做到知其所以然。因此打算写这篇笔记,先好好梳理一下参数估计与假设检验的相关内容。 1 总体梳理 先从整体结构上进行一个把握。数理统计的主要任务是通过样本的信息推断总体的信息,即统计推断工作。统计推断主要有两大类问题:参数估计和假设检验。它们都建立在抽样分布理论的基础之上,但角
大数据(十二):方差分析和参数估计
专栏介绍 结合自身经验和内部资料总结的Python教程,每天3-5章,最短1个月就能全方位的完成Python的学习并进行实战开发,学完了定能成为大佬!加油吧!卷起来! 全部文章请访问专栏:《Python全栈教程(0基础)》 再推荐一下最近热更的:《大厂测试高频面试题详解》 该专栏对近年高频测试相关面试题做详细解答,结合自己多年工作经验,以及同行大佬指导总结出来的。旨在帮助测试、python方面
机器学习---最大似然估计和贝叶斯参数估计
1. 估计 贝叶斯框架下的数据收集,在以下条件下我们可以设计一个可选择的分类器 : P(wi) (先验);P(x | wi) (类条件密度) 但是。我们很少能够完整的得到这些信息! 从一个传统的样本中设计一个分类器: ①先验估计不成问题 ②对类条件密度的估计存在两个问题:1)样本对于类条件估计太少了;2) 特征空间维数太大 了,计算复杂度太高。 如果可以将类条件密度参数化,则可以显
参数估计(一)(点估计)
文章目录 点估计和估计量的求法点估计概念矩估计法极大似然估计法 参考文献 参数估计是数理统计中重要的基本问题之一。通常,称参数的可容许值的全体为参数空间,并记为 Θ \Theta Θ。所谓参数估计就是由样本对总体分布所含的未知参数做出估计。另外,在有些实际问题中,由于事先并不知道总体 X X X 的分布类型,而要对其某些数字特征,如均值、方差等做出估计,习惯上也把这些数字特征
[统计学笔记] (六) 参数估计
(六)参数估计 (Parameter Estimation) 参数估计是推断统计的重要内容之一。它是在抽样及抽样分布的基础上,根据样本统计量来推断所关心的总体参数。 人们常常需要根据手中的数据,分析或推断数据反映的本质规律。即根据样本数据如何选择统计量去推断总体的分布或数字特征等。统计推断是数理统计研究的核心问题。所谓统计推断是指根据样本对总体分布或分布的数字特征等作出合理的推断。它是统计推断






![[闲聊统计]之参数估计是什么?(上)](https://img-blog.csdnimg.cn/direct/6d74922b88e64196b24552da57748bd6.png)