【计算机视觉】Lecture 14：参数估计

本文主要是介绍【计算机视觉】Lecture 14：参数估计，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

总结：变换

参数估计

我们将会讨论以下方面的参数估计：

1. 几何模型（如直线、平面、曲面）
2. 几何变换（我们讨论过的任何参数化变换）

最小二乘法是解决这两个问题的通用策略！

参数估计：拟合几何模型

总体思路：

1. 希望使模型适合原始图像特征（数据）：特征可以是点，边缘，甚至区域
2. 参数化模型：模型例子是Rn的一个元素，也就是模型实例 = （a1， a2，…，an）
3. 定义一个误差函数E（模型i，数据），该函数测量给定模型实例对数据的描述程度（好坏）
4. 求解最小化E的模型实例

示例：直线拟合

总体思路：
1. 希望使模型适合原始图像特征（数据）：特征可以是点，边缘，甚至区域
2. 参数化模型：模型例子是Rn的一个元素，也就是模型实例 = （a1， a2，…，an）
3. 定义一个误差函数E（模型i，数据），该函数测量给定模型实例对数据的描述程度（好坏）
4. 求解最小化E的模型实例

点特征数据（第一步）

点特征 = {(xi, yi) | i = 1,…,n}

示例：直线拟合

总体思路：

1. 希望使模型适合原始图像特征（数据）：特征可以使点，边缘，甚至区域
   2. 参数化模型：模型例子是Rn的一个元素，也就是模型实例 = （a1， a2，…，an）
2. 定义一个误差函数E（模型i，数据），该函数测量给定模型实例对数据的描述程度（好坏）
3. 求解最小化E的模型实例

直线参数化（第二步）

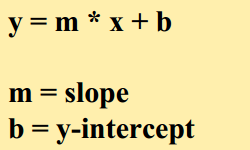
b横穿y轴

模型实例 = （m, b）

示例：直线拟合

总体思路：

1. 希望使模型适合原始图像特征（数据）：特征可以使点，边缘，甚至区域
2. 参数化模型：模型例子是Rn的一个元素，也就是模型实例 = （a1， a2，…，an）
   2. 定义一个误差函数E（模型i，数据），该函数测量给定模型实例对数据的描述程度（好坏）
3. 求解最小化E的模型实例

最小二乘法（第三步）

最小二乘只是众多误差函数中的一种

1. 给定直线（m, b）
2. 点（xi，yi）到直线的距离是垂直距离

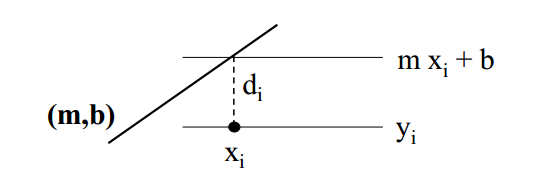
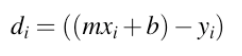
3. E是所有点的平方距离之和

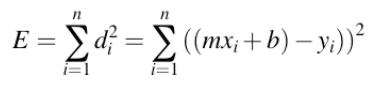
示例：直线拟合

总体思路：

1. 希望使模型适合原始图像特征（数据）：特征可以使点，边缘，甚至区域
2. 参数化模型：模型例子是Rn的一个元素，也就是模型实例 = （a1， a2，…，an）
3. 定义一个误差函数E（模型i，数据），该函数测量给定模型实例对数据的描述程度（好坏）
   3. 求解最小化E的模型实例

求极值的微积分（第四步）

1. 分别求 E 关于 m 和 b 的一阶导数
2. 将方程设为零

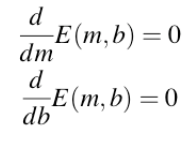
3. 求解 m 和 b （线性回归的等价性）

最小二乘解

参数化问题

我们的参数化有一个问题，即（m，b）对于垂直线是未定义的

更一般的直线参数化是下面这样的

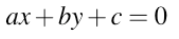
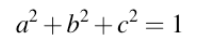
代数距离的最小二乘法

代数距离 ：

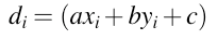
误差函数求导

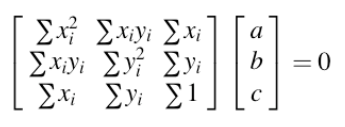
（a，b，c）是与最小特征值相关联的特征向量
（只有在没有噪声的情况下才是0，因此所有的点都准确地在一条直线上）

请注意，与线性回归直线（在这种情况下）有很大不同，但我们可以放心，当我们的程序看到一条垂直线时，它不会凸起！

代数最小二乘问题

注意：我没有在图上画出误差向量

那是因为我不知道怎么画…

代数距离的主要问题：很难说清楚你在最小化什么，因为代数距离是有很少物理意义的量

正交最小二乘法

最小化正交（几何）距离。

在物理上有意义，但很难推导

表示：

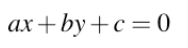
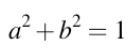
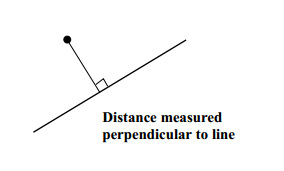
垂直于直线测量的距离

正交最小二乘法

很难推导。

关键洞察：最佳的拟合直线必须会通过点集的质心！

将质心移到原点。

这就将问题简化为寻找垂直于直线的单位向量：寻找（a，b）使得 a平方 + b平方 =1

这将是点的散射矩阵的最小特征向量。

最后，解出c

正交最小二乘解

这个“距离”是指我们直觉上所期望的

（即到线上最近点的距离，或到线上的最小距离）

参数估计：估计变换

假设我们找到了两幅图像之间的匹配点，我们认为它们是通过一些参数化变换（例如平移；尺度欧几里德；仿射）相关联的。我们如何估计此变换的参数？

基本策略
基于对应点的最小二乘估计

两个重要（相关）问题：
多少自由度？
需要多少个对应点？

例子：平移估计

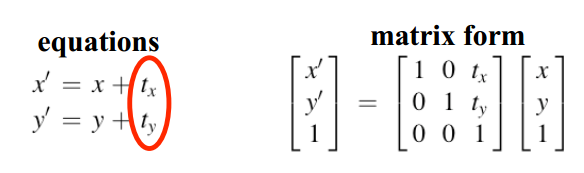
多少自由度？
有多少自变量？
两个

需要多少个对应点？
每个对应关系提供两个方程 (x, y)=>(x’, y’)

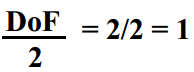
例子：平移估计

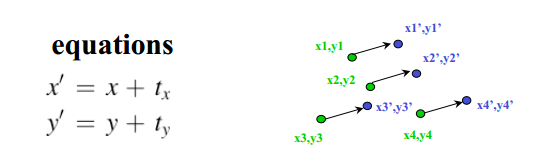
最小二乘估计：

最小化

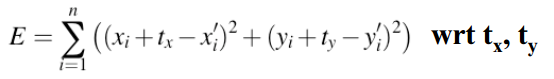
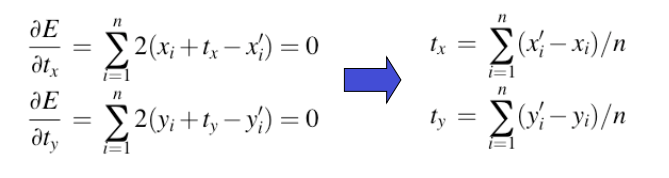
尝试另一个例子

相似变换

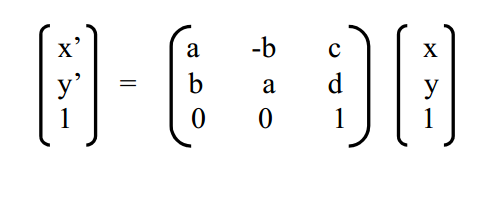
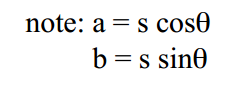
实际问题

一旦我们估计了一个变换，我们如何（反）映射图像像素值来产生一个新的图像

映射&双线性插值

给定两个图像（坐标系）之间的变换，我们希望将一个图像“映射（warp）”到另一个图像的坐标系中。

我们将我们要映射的坐标系称为“源source”图像

我们将要映射到的坐标系称为“目标destination”图像。

映射例子

在这个例子中的变换是射影变换（一般的 3x3 矩阵，在齐次坐标系上运算）

正向映射

在源图像上的每个像素x
以H（x）的形式确定此像素的去向
为目标像素上色

正向映射问题

会留下空隙，这是一个比较大的问题（因为映射有放大作用）

逆向映射（没有空隙）

在目标图像上的每个像素x
以H-1（x）的形式确定此像素的来源
从那个地方获得颜色

插值

我们所说的“从那个地方获得颜色”是什么意思？
考虑灰度值。在（x, y）处的灰度值是什么？

最近的邻域：

取离中心最近的那个像素的颜色。

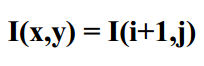
双线性插值

我们所说的“从那个地方获得颜色”是什么意思？
考虑灰度值。在（x, y）处的灰度值是什么？

双线性插值：加权平均

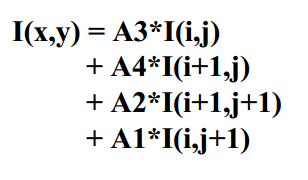
双线性插值，数学描述

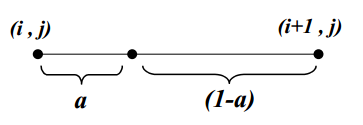
首先，考虑线性插值

初始化：给定两个像素值，它们之间的某个中间点的值应该是多少？

如果接近（i，j），则灰度值应该类似于 I(i，j)

如果与两者距离相等，则应该为两个灰度值的平均值

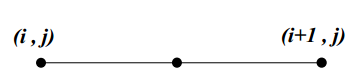
如果接近 （i+1, j），则灰度值应该类似于 I(i+1, j)

线性插值

回忆：平面上直线求解

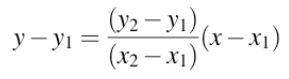
实例化：

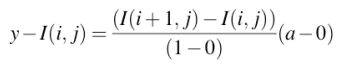
求解：

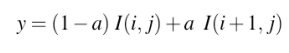
双线性插值，数学描述

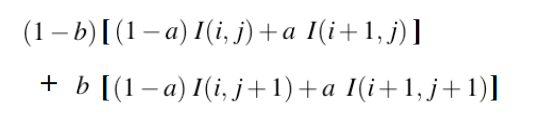
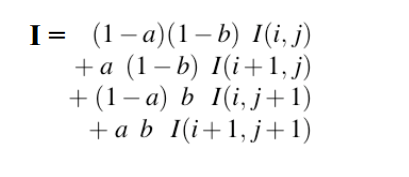
Matlab中的图像映射

interp2是 Matlab 内置的图像映射函数

用法： interp2(X,Y,Z,XI,YI)

使用Interp2的技巧

为了达到我们的目的，我们可以假设 X 和 Y 是正交的图像像素坐标

简单用法： interp2(Z,XI,YI)

它是如何工作的？

考虑计算R行和C列的ZI值。

XI 和 YI 是和 ZI 尺寸相同的两个数列
对给定行列（R, C），数值 (XI(R, C), YI(R, C)) 表示为获取的原始图像上 (X，Y) 坐标处的值
最终结果是： Z(YI(R, C), XI(R, C))

interp2 处理了双线性插值，以防 YI(R, C) 和 XI(R, C) 不是整数坐标。

interp2有可选参数来更改计算插值的方式。我们可以使用默认值，即双线性插值。

Meshgrid

使用interp2时的一个有用函数是meshgrid

Interp2例子

Interp2例子

易混淆点

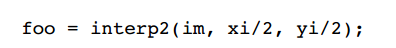
将坐标值除以2是将图像放大尺度2

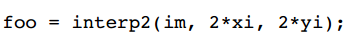
将坐标值乘以2是将图像缩小尺度2

Interp2希望反坐标变换为所需的几何变换（它使用逆向映射）

Interp2例子

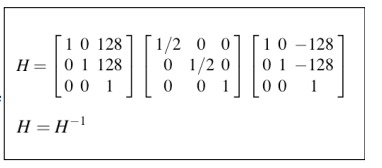
一个更复杂的例子：缩小尺度2，但围绕图像中心（128, 128），而不是（0, 0）

回忆变换矩阵级联

这指定了我们希望原始图像如何映射到新图像中。

Interp2想知道新的图像坐标如何映射回原始图像坐标。

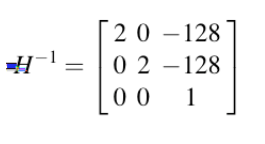
更一般的（比如齐次坐标系中任何 3×3 变换矩阵）

这篇关于【计算机视觉】Lecture 14：参数估计的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---