【概率论】期末复习笔记：参数估计

一、点估计

1. 估计量的概念

点估计：设总体$X$的分布函数为$F(x;{\theta }_1,{\theta }_2,\cdots ,{\theta }_l)$，其中${\theta }_1,{\theta }_2,\cdots ,{\theta }_l$是待估计的未知参数，$(X_1,X_2,\cdots ,X_n)$是来自总体$X$的样本，$(x_1,x_2,\cdots ,x_n)$是相应的样本值，点估计问题就是要构造$l$个适当的统计量${\hat{\theta }}_i(X_1,X_2,\cdots ,X_n)(i=1,2,\cdots ,l)$，分别用观测值${\hat{\theta }}_i(x_1,x_2,\cdots ,x_n)$作为未知参数${\theta }_i$的估计值。
估计量：估计用的统计量${\hat{\theta }}_i(X_1,X_2,\cdots ,X_n)$
估计值：估计量的观测值${\hat{\theta }}_i(x_1,x_2,\cdots ,x_n)$
在不致混淆的情况下统称估计量和估计值为估计，并都简记为${\hat{\theta }}_i$。

估计量是样本的函数，是随机变量，不同的样本值得到的估计值往往是不同的。

2. 估计量的求法

矩估计法

设总体$X$的前$l$阶原点矩${\alpha }_k=E\left(X^k\right)(k=1,2,\cdots ,l)$存在，且都是${\theta }_1,{\theta }_2,\cdots ,{\theta }_l$的函数，即${\alpha }_k={\alpha }_k({\theta }_1,{\theta }_2,\cdots ,{\theta }_l)$。把总体原点矩用样本原点矩代替（${\alpha }_k\to A_k$），未知参数用其估计量代替（${\theta }_i\to {\hat{\theta }}_i$），得$$\{\begin{array}{l}{\alpha }_1\left({\hat{\theta }}_1,{\hat{\theta }}_2,\cdots ,{\hat{\theta }}_l\right)=A_1\\ {\alpha }_2\left({\hat{\theta }}_1,{\hat{\theta }}_2,\cdots ,{\hat{\theta }}_l\right)=A_2\\ \cdots \\ {\alpha }_l\left({\hat{\theta }}_1,{\hat{\theta }}_2,\cdots ,{\hat{\theta }}_l\right)=A_l\end{array}$$解此方程组可得${\hat{\theta }}_1,{\hat{\theta }}_2,\cdots ,{\hat{\theta }}_l$（是$A_1,A_2,\cdots ,A_k$的函数），并将它们分别作为${\theta }_1,{\theta }_2,\cdots ,{\theta }_l$的估计量。$A_1$一般写作$\overline{X}$。

矩估计法的理论依据是大数定律，当$n$充分大时，样本矩$A_k$以很大的概率落在总体矩${\alpha }_k$的附近，因此可用$A_k$作为${\alpha }_k$的矩估计量。

例 $X\text{~}U(0,\theta )$，求$\theta$的矩估计量。
解：我们知道$${\alpha }_1=E(X)=\frac{\theta }{2}$$把${\alpha }_1$换成$A_1$（$\overline{X}$），$\theta$换成$\hat{\theta }$得$$\overline{X}=\frac{\hat{\theta }}{2}$$因此$\theta$的矩估计量为$\hat{\theta }=2\overline{X}$。

矩估计法不必知道总体的分布，优点是简单直接，但缺点是只利用了总体的局部特性而没有充分利用总体的信息。

最大似然估计法

思想：若存在某一分布，使得在此分布下抽中$(x_1,x_2,\cdots ,x_n)$的概率最大，则认为$(x_1,x_2,\cdots ,x_n)$来自这一分布。

似然函数：若总体$X$是离散型或连续型随机变量，其分布律为 P { X = x } = p ( x ; θ 1 , θ 2 , ⋯ , θ l ) P\{X=x\}=p(x;\theta_1,\theta_2,\cdots,\theta_l) P{X=x}=p(x;θ1​,θ2​,⋯,θl​)，或其概率密度为$f(x;{\theta }_1,{\theta }_2,\cdots ,{\theta }_l)$，其中${\theta }_1,{\theta }_2,\cdots ,{\theta }_l$为未知参数，在参数空间$\Theta$内取值，变量$x$在随机变量$X$的可能取值范围内取值。设$(X_1,X_2,\cdots ,X_n)$是来自总体$X$的样本，则$(X_1,X_2,\cdots ,X_n)$的分布律为 L ( x 1 , x 2 , ⋯ , x n ; θ 1 , θ 2 , ⋯ , θ l ) = P { X 1 = x 1 , X 2 = x 2 , ⋯ , X n = x n } = ∏ i = 1 n p ( x i ; θ 1 , θ 2 , ⋯ , θ l ) \begin{aligned} L(x_1,x_2,\cdots,x_n;\theta_1,\theta_2,\cdots,\theta_l)&=P\{X_1=x_1,X_2=x_2,\cdots,X_n=x_n\}\\ &=\prod\limits_{i=1}^n p(x_i;\theta_1,\theta_2,\cdots,\theta_l) \end{aligned} L(x1​,x2​,⋯,xn​;θ1​,θ2​,⋯,θl​)​=P{X1​=x1​,X2​=x2​,⋯,Xn​=xn​}=i=1∏n​p(xi​;θ1​,θ2​,⋯,θl​)​或概率密度为$$L(x_1,x_2,\cdots ,x_n;{\theta }_1,{\theta }_2,\cdots ,{\theta }_l)=\prod _{i=1}^{n}f(x_i;{\theta }_1,{\theta }_2,\cdots ,{\theta }_l)$$当固定$(x_1,x_2,\cdots ,x_n)$，把$L$看成是${\theta }_1,{\theta }_2,\cdots ,{\theta }_l$的定义于$\Theta$上的函数时，它称为参数${\theta }_1,{\theta }_2,\cdots ,{\theta }_l$的似然函数，并简记为$L({\theta }_1,{\theta }_2,\cdots ,{\theta }_l)$。即：似然函数就是样本的分布律/概率密度，然后看成参数的函数。
对数似然函数：似然函数的对数$\ln L({\theta }_1,{\theta }_2,\cdots ,{\theta }_l)$称为对数似然函数。

最大似然估计法：得到样本值$(x_1,x_2,\cdots ,x_n)$后，取${\hat{\theta }}_1,{\hat{\theta }}_2,\cdots ,{\hat{\theta }}_n$使得$$L({\hat{\theta }}_1,{\hat{\theta }}_2,\cdots ,{\hat{\theta }}_n)=\underset{({\theta }_1,{\theta }_2,\cdots ,{\theta }_l)\in \Theta }{\max }L({\theta }_1,{\theta }_2,\cdots ,{\theta }_l)$$这样得到的${\hat{\theta }}_1,{\hat{\theta }}_2,\cdots ,{\hat{\theta }}_n$与样本值$(x_1,x_2,\cdots ,x_n)$有关，记为${\hat{\theta }}_i={\hat{\theta }}_i(x_1,x_2,\cdots ,x_n)$，并称为参数${\theta }_i(i=1,2,\cdots ,l)$的最大似然估计值，而相应的统计量${\hat{\theta }}_i={\hat{\theta }}_i(X_1,X_2,\cdots ,X_n)(i=1,2,\cdots ,l)$称为参数${\theta }_i$的最大似然估计量。

由于$\ln x$是$x$的单调增函数，所以$L$取最大的时候$\ln L$也取最大，我们也可以考察$\ln L$的最大值。

在很多时候，$L$和$\ln L$关于参数${\theta }_1,{\theta }_2,\cdots ,{\theta }_l$的偏导数存在，此时${\hat{\theta }}_1,{\hat{\theta }}_2,\cdots ,{\hat{\theta }}_n$可从似然方程$$\{\begin{array}{l}\frac{\partial L({\theta }_1,{\theta }_2,\cdots ,{\theta }_l)}{\partial {\theta }_1}=0\\ \frac{\partial L({\theta }_1,{\theta }_2,\cdots ,{\theta }_l)}{\partial {\theta }_2}=0\\ \cdots \\ \frac{\partial L({\theta }_1,{\theta }_2,\cdots ,{\theta }_l)}{\partial {\theta }_l}=0\end{array}$$或对数似然方程$$\{\begin{array}{l}\frac{\partial \ln L({\theta }_1,{\theta }_2,\cdots ,{\theta }_l)}{\partial {\theta }_1}=0\\ \frac{\partial \ln L({\theta }_1,{\theta }_2,\cdots ,{\theta }_l)}{\partial {\theta }_2}=0\\ \cdots \\ \frac{\partial \ln L({\theta }_1,{\theta }_2,\cdots ,{\theta }_l)}{\partial {\theta }_l}=0\end{array}$$中解出。

例 设$X\text{~}U(0,\theta )$，求$\theta$的最大似然估计量。
解：$X$的概率密度为$$f(x;\theta )=\{\begin{array}{ll}\frac{1}{\theta },& 0\le x\le \theta \\ 0,& \text{其他}\end{array}$$则样本$(X_1,X_2,\cdots ,X_n)$的联合概率密度为$$f(x_1,x_2,\cdots ,x_n;\theta )=\prod _{i=1}^{n}f(x_i;\theta )=\{\begin{array}{ll}\frac{1}{{\theta }^n},& 0\le x_1,x_2,\cdots ,x_n\le \theta \\ 0,& \text{其他}\end{array}$$把它看作$\theta$的函数（$x_1,x_2,\cdots ,x_n$为已知），那么$\theta$的似然函数为 L ( θ ) = { 1 θ n , θ ≥ max ⁡ { x 1 , x 2 , ⋯ , x n } 0 , 其他 L(\theta)=\begin{cases} \frac{1}{\theta^n},&\theta\ge\max\{x_1,x_2,\cdots,x_n\}\\ 0,&\text{其他} \end{cases} L(θ)={θn1​,0,​θ≥max{x1​,x2​,⋯,xn​}其他​这个函数我们不用求导就能求出最大值。首先，它在 θ ≥ max ⁡ { x 1 , x 2 , ⋯ , x n } \theta\ge\max\{x_1,x_2,\cdots,x_n\} θ≥max{x1​,x2​,⋯,xn​}时才是正数；其次，在$\theta$满足这个条件的情况下，因为${\theta }^n$在分母，所以我们希望$\theta$尽量小。因此当 θ = max ⁡ { x 1 , x 2 , ⋯ , x n } \theta=\max\{x_1,x_2,\cdots,x_n\} θ=max{x1​,x2​,⋯,xn​}时$L(\theta )$取最大值。$\theta$的最大似然估计量为$\hat{\theta }=X_{(n)}$。这与矩估计法求得的估计量不同。

二、估计量的评选标准

1. 无偏性

无偏估计量：设$(X_1,X_2,\cdots ,X_n)$是来自总体$X$的一个样本，$\theta$是包含在$X$的分布中的未知参数，$\theta$的取值范围为$\Theta$，$\hat{\theta }=\hat{\theta }(X_1,X_2,\cdots ,X_n)$是$\theta$的一个估计量。若$\forall \theta \in \Theta$，$E\left(\hat{\theta }\right)=\theta$，则称$\hat{\theta }$是$\theta$的一个无偏估计量。
有偏估计量：有偏差的估计量，其中偏差（简称偏）等于$E\left(\hat{\theta }\right)-\theta$。
渐进无偏估计量：若$E\left(\hat{\theta }\right)-\theta \ne 0$，但当样本容量$n\to \infty$时，有$\underset{n\to \infty }{\lim }\left[E\left(\hat{\theta }\right)-\theta \right]=0$，则称$\hat{\theta }$是$\theta$的渐近无偏估计量。

设$(X_1,X_2,\cdots ,X_n)$是来自总体$X$的样本，无论$X$服从什么分布，都有
(1) 若$E(X)=\mu$存在，则样本均值$\overline{X}$是$E(X)$的无偏估计量；
(2) 若$D(X)={\sigma }^2$存在，则样本方差$S^2$是${\sigma }^2$的无偏估计量；
(3) 若总体$k$阶矩$E\left(X^k\right)={\alpha }_k$存在，则$k$阶样本原点矩$A_k=\frac{1}{k}\sum _{i=1}^n{X}_i^k$是$k$阶总体原点矩${\alpha }_k$的无偏估计量。

例 可以证明，设总体$X\text{~}U(0,\theta )$，参数$\theta >0$，则$2\overline{X}$和$\frac{n+1}{n}{X}_{(n)}$都是$\theta$的无偏估计量。

虽然$S^2$是${\sigma }^2$的无偏估计量，但$S$不是$\sigma$的无偏估计量，$\sqrt{\frac{n-1}{2}}\frac{\Gamma \left(\frac{n-1}{2}\right)}{\Gamma \left(\frac{n}{2}\right)}S$才是$\sigma$的无偏估计量。这说明，若$\hat{\theta }$是$\theta$的无偏估计量，一般情况下，$g\left(\hat{\theta }\right)$不是$\theta$的无偏估计量，除非$g$是线性函数。

2. 有效性

无偏估计量不一定是唯一的，所以我们需要选取其中取值最集中的，即方差最小的作为最好的估计量。

有效性：设${\hat{\theta }}_1$和${\hat{\theta }}_2$都是$\theta$的无偏估计量，若$D\left({\hat{\theta }}_1\right)\le D\left({\hat{\theta }}_2\right)$，则称${\hat{\theta }}_1$较${\hat{\theta }}_2$有效。

例 设$X\text{~}U(0,\theta )$，则${\hat{\theta }}_2=\frac{n+1}{n}{X}_{(n)}$比${\hat{\theta }}_1=2\overline{X}$有效（$D\left({\hat{\theta }}_1\right)=\frac{{\theta }^2}{3n}>D\left({\hat{\theta }}_2\right)=\frac{{\theta }^2}{n(n+2)}$）。

最小方差无偏估计量：在所有估计量中方差最小的无偏估计量

3. 相合性

相合估计量/一致估计量：设$\hat{\theta }=\hat{\theta }(X_1,X_2,\cdots ,X_n)$是参数$\theta$的估计量，如果当$n\to \infty$时，$\hat{\theta }$依概率收敛于$\theta$，即$$\forall \epsilon >0,\underset{n\to \infty }{\lim }P\left\{\left|\hat{\theta }-\theta \right|<\epsilon \right\}=1$$则称$\hat{\theta }$为$\theta$的相合估计量/一致估计量，并记$(p)\underset{n\to \infty }{\lim }\hat{\theta }=\theta$或$\hat{\theta }\stackrel{P}{⟶}\theta (n\to \infty )$。
均方相合估计量：如果当$n\to \infty$时，$\hat{\theta }$均方收敛于$\theta$，即$$\underset{n\to \infty }{\lim }E\left[{\left(\hat{\theta }-\theta \right)}^2\right]=0$$则称$\hat{\theta }$为$\theta$的均方相合估计量，并记$(\text{m. s. })\underset{n\to \infty }{\lim }\hat{\theta }=\theta$或$\hat{\theta }\stackrel{L^2}{⟶}\theta (n\to \infty )$。

相合性是对估计量的最基本的要求，它要求当样本容量无限增加时，用估计量估计参数可以达到任意小的精度。

可以证明，常见的矩估计量都是相合估计量（例如$A_k\to {\alpha }_k$、$\overline{X}\to E(X)$、$S^2\to {\sigma }^2$、$S\to \sigma$）。均方相合估计量一定是相合估计量，但反之不一定成立。

一个重要事实：设总体$X$的分布函数为$F(x)$，$(X_1,X_2,\cdots ,X_n)$为来自总体$X$的样本，$F_n(X)=\frac{1}{n}\sum _{i=1}^n[X_i\le x]$是经验分布函数，则对任意固定的$x$，$F_n(x)$是$F(x)$的无偏估计量、相合估计量、均方相合估计量。

总结

无偏性：$E\left(\hat{\theta }\right)=\theta$
有效性：方差越小越好
相合性：依概率收敛（样本容量足够大时估计值与真实值之间的差距可以任意小）

三、区间估计

1. 双侧区间估计

$$\underset{\Downarrow }{P\left\{{\hat{\theta }}_1(X_1,X_2,\cdots ,X_n)<\theta <{\hat{\theta }}_2(X_1,X_2,\cdots ,X_n)\right\}=1-\alpha }$$随机区间$\left({\hat{\theta }}_1,{\hat{\theta }}_2\right)$为参数$\theta$的置信度为$1-\alpha$的双侧置信区间。
${\hat{\theta }}_1$：置信下限
${\hat{\theta }}_2$：置信上限
$1-\alpha$：置信度
$\alpha$：区间$\left({\hat{\theta }}_1,{\hat{\theta }}_2\right)$不包含$\theta$的概率（一般很小）

在置信度$1-\alpha$给定的情况下，置信区间的长度$E\left({\hat{\theta }}_2-{\hat{\theta }}_1\right)$越小越好。

求未知参数$\theta$的双侧置信区间的具体做法：

(1) 寻求枢轴量$Z=Z\left(X_1,X_2,\cdots ,X_n,\theta \right)$，我们需要知道$Z$的分布，并且此分布不依赖于任何未知参数，也不依赖于$\theta$。
(2) 对于给定的置信度$1-\alpha$，求出两个常数$k_1,k_2$使得 P { k 1 < Z < k 2 } = 1 − α P\{k_1<Z<k_2\}=1-\alpha P{k1​<Z<k2​}=1−α。
(3) $k_1<Z<k_2\stackrel{\text{改写}}{⟶}{\hat{\theta }}_1<\theta <{\hat{\theta }}_2$：$\left({\hat{\theta }}_1,{\hat{\theta }}_2\right)$是置信度为$1-\alpha$的置信区间。
(4) 根据样本值计算${\hat{\theta }}_1,{\hat{\theta }}_2$的具体值。

例 设$X\text{~}N(\mu ,{\sigma }^2)$，${\sigma }^2$已知，$\mu$未知，求参数$\mu$的置信度为$1-\alpha$的置信区间。
解：取枢轴量$U=\frac{\overline{X}-\mu }{\sigma /\sqrt{n}}\text{~}N(0,1)$，可以看出$N(0,1)$不依赖任何参数。
现在要找到$k_1,k_2$使得 P { k 1 < U < k 2 } = 1 − α P\left\{k_1<U<k_2\right\}=1-\alpha P{k1​<U<k2​}=1−α，一般取$k_1=-u_{\alpha /2}$，$k_2=u_{\alpha /2}$。注意到$-u_{\alpha /2}=u_{1-\alpha /2}$，我们有 P { k 1 < U < k 2 } = 1 − P { U ≥ k 2 } − P { U ≤ k 1 } = 1 − α 2 − ( 1 − P { U > k 1 } ) = 1 − α 2 − [ 1 − ( 1 − α 2 ) ] = α \begin{aligned} P\{k_1<U<k_2\}&=1-P\{U\ge k_2\}-P\{U\le k_1\}\\ &=1-\frac{\alpha}{2}-\left(1-P\left\{U>k_1\right\}\right)\\ &=1-\frac{\alpha}{2}-\left[1-\left(1-\frac{\alpha}{2}\right)\right]\\ &=\alpha \end{aligned} P{k1​<U<k2​}​=1−P{U≥k2​}−P{U≤k1​}=1−2α​−(1−P{U>k1​})=1−2α​−[1−(1−2α​)]=α​

既然$P\left\{-u_{\alpha /2}<\frac{\overline{X}-\mu }{\sigma /\sqrt{n}}<u_{\alpha /2}\right\}=1-\alpha$，那么$$\begin{array}{rl}P\left\{-\frac{\sqrt{n}}{\sigma }{u}_{\alpha /2}<\overline{X}-\mu <\frac{\sqrt{n}}{\sigma }{u}_{\alpha /2}\right\}& =1-\alpha \\ P\left\{\overline{X}-\frac{\sqrt{n}}{\sigma }{u}_{\alpha /2}<\mu <\overline{X}+\frac{\sqrt{n}}{\sigma }{u}_{\alpha /2}\right\}& =1-\alpha \end{array}$$于是得$\mu$的置信度为$1-\alpha$的置信区间为$\left(\overline{X}-\frac{\sqrt{n}}{\sigma }{u}_{\alpha /2},\overline{X}+\frac{\sqrt{n}}{\sigma }{u}_{\alpha /2}\right)$。

其实，选取枢轴量的过程就是从$X$的分布中剔除参数$\theta$的影响的过程。$X$的分布受$\theta$影响，我们就需要消除这种影响，所以我们提出统计量$Z$，它的分布是完全确定的，只有这样我们才能确定参数$k_1,k_2$。如果$X$的分布不是确定的，那么我们很难求出置信区间。

2. 单侧区间估计

P { θ ‾ ( X 1 , X 2 , ⋯ , X n ) < θ } = 1 − α ⟹ ( θ ‾ , + ∞ ) P\left\{\underline{\theta}(X_1,X_2,\cdots,X_n)<\theta\right\}=1-\alpha\implies\left(\underline{\theta},+\infty\right) P{θ​(X1​,X2​,⋯,Xn​)<θ}=1−α⟹(θ​,+∞)是$\theta$的置信度为$1-\alpha$的单侧置信区间，$\underline{\theta }$为置信下界；
$P\left\{\theta <\overline{\theta }(X_1,X_2,\cdots ,X_n)\right\}=1-\alpha ⟹\left(-\infty ,\overline{\theta }\right)$是$\theta$的置信度为$1-\alpha$的单侧置信区间，$\overline{\theta }$为置信上界。

即：$\left(\underline{\theta },+\infty \right)$包含$\theta$的概率为$1-\alpha$，$\left(-\infty ,\overline{\theta }\right)$包含$\theta$的概率为$1-\alpha$。

在置信度$1-\alpha$给定的情况下，置信下界越大越好，置信上界越小越好。

四、正态总体参数的区间估计

对于单个总体的情形，我们设$X\text{~}N(\mu ,{\sigma }^2)$；对于两个总体的情形，我们设$X\text{~}N({\mu }_1,{\sigma }_1^2)$，$Y\text{~}N({\mu }_2,{\sigma }_2^2)$。$X$的样本容量为$n$，样本方差为$S_X^2$；$Y$的样本容量为$m$，样本方差为$S_Y^2$。

下面是单个总体的情形（$X\text{~}N(\mu ,{\sigma }^2)$）。

${\sigma }^2\text{已知，考察}\mu$

枢轴量$U=\frac{\sqrt{n}\left(\overline{X}-\mu \right)}{\sigma }\text{~}N(0,1)$

注意$P\left\{-u_{\alpha /2}<U<u_{\alpha /2}\right\}=1-\alpha$
P { U < u α } = 1 − α P\left\{U<u_\alpha\right\}=1-\alpha P{U<uα​}=1−α
P { U > − u α } = 1 − α P\left\{U>-u_\alpha\right\}=1-\alpha P{U>−uα​}=1−α

${\sigma }^2\text{未知，考察}\mu$

枢轴量$T=\frac{\sqrt{n}\left(\overline{X}-\mu \right)}{S}\text{~}t(n-1)$

注意$P\left\{-t_{\alpha /2}<T<t_{\alpha /2}\right\}=1-\alpha$
P { T < t α } = 1 − α P\left\{T<t_\alpha\right\}=1-\alpha P{T<tα​}=1−α
P { T > − t α } = 1 − α P\left\{T>-t_\alpha\right\}=1-\alpha P{T>−tα​}=1−α

$\mu \text{已知，考察}{\sigma }^2$

枢轴量${\chi }^2=\frac{\sum _{i=1}^n{\left(X_i-\mu \right)}^2}{{\sigma }^2}\text{~}{\chi }^2(n)$

$\mu \text{未知，考察}{\sigma }^2$

枢轴量${\chi }^2=\frac{\sum _{i=1}^n{\left(X_i-\overline{X}\right)}^2}{{\sigma }^2}=\frac{(n-1)S^2}{{\sigma }^2}\text{~}{\chi }^2(n-1)$

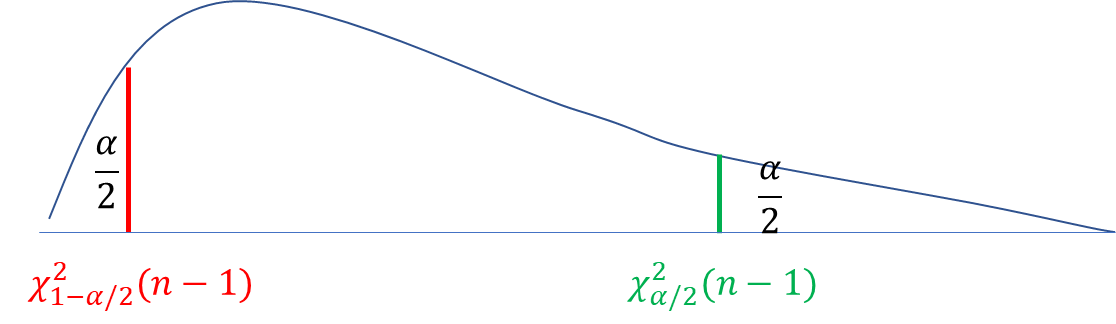
注意$P\left\{{\chi }^2>{\chi }_{\alpha /2}^2(n-1)\right\}=\frac{\alpha }{2}$，$P\left\{{\chi }^2>{\chi }_{1-\alpha /2}^2(n-1)\right\}=1-\frac{\alpha }{2}$，故 P { χ 1 − α / 2 2 ( n − 1 ) < χ 2 < χ α / 2 2 ( n − 1 ) } = 1 − α P\{\chi^2_{1-\alpha/2}(n-1)<\chi^2<\chi^2_{\alpha/2}(n-1)\}=1-\alpha P{χ1−α/22​(n−1)<χ2<χα/22​(n−1)}=1−α。
$P\left\{{\chi }^2<{\chi }_{\alpha }^2(n-1)\right\}=1-\alpha$
$P\left\{{\chi }^2>{\chi }_{1-\alpha }^2(n-1)\right\}=1-\alpha$

下面是两个总体的情形（$X\text{~}N({\mu }_1,{\sigma }_1^2)$，$Y\text{~}N({\mu }_2,{\sigma }_2^2)$）。

${\sigma }_1^2,{\sigma }_2^2\text{已知，考察}{\mu }_1-{\mu }_2$

枢轴量$U=\frac{\left(\overline{X}-\overline{Y}\right)-({\mu }_1-{\mu }_2)}{\sqrt{\frac{{\sigma }_1^2}{n}+\frac{{\sigma }_2^2}{m}}}\text{~}N(0,1)$

注意$D\left(\overline{X}-\overline{Y}\right)=\frac{{\sigma }_1^2}{n}+\frac{{\sigma }_2^2}{m}$。

${\sigma }_1^2={\sigma }_2^2\text{未知，考察}{\mu }_1-{\mu }_2$

枢轴量$T=\frac{\left(\overline{X}-\overline{Y}\right)-({\mu }_1-{\mu }_2)}{S_W\sqrt{\frac{1}{n}+\frac{1}{m}}}\text{~}t(n+m-2)$，其中$S_W=\sqrt{\frac{(n-1)S_X^2+(m-1)S_Y^2}{n+m-2}}$

注意$U=\frac{\left(\overline{X}-\overline{Y}\right)-({\mu }_1-{\mu }_2)}{\sigma \sqrt{\frac{1}{n}+\frac{1}{m}}}\text{~}N(0,1)$，$V=\frac{(n-1)S_X^2+(m-1)S_Y^2}{{\sigma }^2}\text{~}{\chi }^2(n+m-2)$。

${\mu }_1,{\mu }_2\text{已知，考察}\frac{{\sigma }_1^2}{{\sigma }_2^2}$

枢轴量$F=\frac{\sum _{i=1}^n\frac{{(X_i-{\mu }_1)}^2}{{\sigma }_1^2}/n}{\sum _{j=1}^m\frac{{(Y_j-{\mu }_2)}^2}{{\sigma }_2^2}/m}=\frac{{\sigma }_2^2}{{\sigma }_1^2}\frac{m\sum _{i=1}^n{(X_i-{\mu }_1)}^2}{n\sum _{j=1}^m{(Y_j-{\mu }_2)}^2}\text{~}F(n,m)$

${\mu }_1,{\mu }_2\text{未知，考察}\frac{{\sigma }_1^2}{{\sigma }_2^2}$

枢轴量$F=\frac{{\sigma }_2^2}{{\sigma }_1^2}\frac{S_X^2}{S_Y^2}\text{~}F(n-1,m-1)$

注意$P\left\{F>F_{\alpha /2}(n-1,m-1)\right\}=\frac{\alpha }{2}$，$P\left\{F>F_{1-\alpha /2}(n-1,m-1)\right\}=1-\frac{\alpha }{2}$，故 P { F 1 − α / 2 ( n − 1 , m − 1 ) < F < F α / 2 ( n − 1 , m − 1 ) } = 1 − α P\{F_{1-\alpha/2}(n-1,m-1)<F<F_{\alpha/2}(n-1,m-1)\}=1-\alpha P{F1−α/2​(n−1,m−1)<F<Fα/2​(n−1,m−1)}=1−α。
P { F < F α ( n − 1 , m − 1 ) } = 1 − α P\left\{F<F_{\alpha}(n-1,m-1)\right\}=1-\alpha P{F<Fα​(n−1,m−1)}=1−α
P { F > F 1 − α ( n − 1 , m − 1 ) } = 1 − α P\left\{F>F_{1-\alpha}(n-1,m-1)\right\}=1-\alpha P{F>F1−α​(n−1,m−1)}=1−α

$t$分布和标准正态分布$N(0,1)$类似，概率密度曲线都是关于$x=0$对称的，$u_{1-\alpha }=-u_{\alpha }$，$t_{1-\alpha }(n)=-t_{\alpha }(n)$；
$F$分布和${\chi }^2$分布类似，概率密度都只在$x>0$时为正。

不论$X$服从何分布，都满足 P { q 1 − α / 2 < X < q α / 2 } = 1 − α P\{q_{1-\alpha/2}<X<q_{\alpha/2}\}=1-\alpha P{q1−α/2​<X<qα/2​}=1−α，其中$q_{\alpha }$表示$X$服从的分布的上侧$\alpha$分位数。

关于自由度是多少，可以这么考虑：如果总体均值$\mu$已知，那么自由度就是样本容量；如果总体均值$\mu$未知，而用样本均值$\overline{X}$代替的话，就要损失一个自由度。对于检验样本均值差时所用的$t$分布，它的自由度是二者的自由度之和。