本文主要是介绍机器学习---最大似然估计和贝叶斯参数估计，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
1. 估计
贝叶斯框架下的数据收集，在以下条件下我们可以设计一个可选择的分类器 :
P(wi) (先验)；P(x | wi) (类条件密度)
但是。我们很少能够完整的得到这些信息!
从一个传统的样本中设计一个分类器：
①先验估计不成问题
②对类条件密度的估计存在两个问题：1）样本对于类条件估计太少了；2） 特征空间维数太大
了，计算复杂度太高。
如果可以将类条件密度参数化，则可以显著降低难度。
例如：P(x | wi)的正态性，P(x | wi) ~ N( mi, Si)，用两个参数表示，这样就将概率密度估计问题转
化为参数估计问题。
最大似然估计 (ML) 和贝叶斯估计；结果通常很接近, 但是方法本质是不同的。
最大似然估计将参数看作是确定的量，只是其值是未知! 通过最大化所观察的样本概率得到最优的
参数—用分析方法。
贝叶斯方法把参数当成服从某种先验概率分布的随机变量，对样本进行观测的过程，就是把先验概
率密度转化成为后验概率密度，使得对于每个新样本，后验概率密度函数在待估参数的真实值附近
形成最大尖峰。在参数估计完后，两种方法都用后验概率P(wi | x)表示分类准则!
2. 最大似然估计
最大似然估计的优点：当样本数目增加时，收敛性质会更好； 比其他可选择的技术更加简单。
2.1 基本原理
假设有c类样本，并且每个样本集的样本都是独立同分布的随机变量；P(x | wj) 形式已知但参数未
知，例如P(x | wj) ~ N( mj, Sj)；记 P(x | wj) º P (x | wj, qj)，其中
使用训练样本提供的信息估计θ = (θ1, θ2, …, θc), 每个 θi (i = 1, 2, …, c) 只和每一类相关 。
假定D包括n个样本, x1, x2,…, xn，
θ的最大似然估计是通过定义最大化P(D | θ)的值，“θ值与实际观察中的训练样本最相符”
最优估计：令
并令
为梯度算子，the gradient operator
我们定义 l(θ) 为对数似然函数：l(θ) = ln P(D | θ)
新问题陈述：求解 θ 为使对数似然最大的值 
对数似然函数l(θθ)显然是依赖于样本集D, 有：
最优求解条件如下：
令
，来求解。
2.2 高斯情况：μ未知
P(xk | μ) ~ N(μ, Σ)：(样本从一组多变量正态分布中提取)
θ = μ，因此：μ的最大似然估计必须满足 
乘Σ并且重新排序, 我们得到：
即训练样本的算术平均值!
结论：如果P(xk | wj) (j = 1, 2, …, c)被假定为d 维特征空间中的高斯分布；然后我们能够估计向量
从而得到最优分类!
2.3 高斯情况：μ和Σ未知
未知 μ 和 σ，对于单样本xk：θ = (θ1, θ2) = (μ, σ2)
对于全部样本，最后得到：
联合公式 (1) 和 (2), 得到如下结果：
3. 贝叶斯估计
在最大似然估计中 θ 被假定为固定值；在贝叶斯估计中 θ 是随机变量
3.1 类条件密度
目标: 计算 P(wi | x, D)，假设样本为D，贝叶斯方程可以写成：
先验概率通常可以事先获得，因此
每个样本只依赖于所属的类，有：
即：只要在每类中，独立计算
就可以确定x的类别。
因此，核心工作就是要估计
3.2 参数分布
假设 
的形式已知, 参数θ的值未知，因此条件概率密度
的函数形式是知道的；假设参
数q是随机变量，先验概率密度函数p(θ)已知，利用贝叶斯公式可以计算后验概率密度函数p(θ|D)；
希望后验概率密度函数p(θ | D) 在θ的真实值附件有非常显著的尖峰，则可以使用后验密度p(θ | D)
估计 θ ；注意到：
如果p(θ|D) 在某个值
附件有非常显著的尖峰，即如果条件概率密度具有一个已知的形式，则利
用已有的训练样本，就能够通过p(θ | D) 对p(x | D) 进行估计。
3.3 高斯过程
单变量情形的 p(μ | D)
复制密度：
其中：
结论：
单变量情形的 p(x|D)：
多变量情形：
复制密度：
其中：
利用：
，
得：
。
利用：
，令y=x-μ。
4. 贝叶斯参数估计一般理论
p(x | D) 的计算可推广于所有能参数化未知密度的情况中，基本假设如下:
假定 p(x | θ) 的形式未知，但是q的值未知。q被假定为满足一个已知的先验密度 P(θ)。
其余的 θ 的信息包含在集合D中，其中D是由n维随机变量x1, x2, …, xn组成的集合，它们服从于概
率密度函数p(x)。
基本的问题是：计算先验密度p(θ | D) ，然后 推导出 p(x | D)。
递归贝叶斯学习：
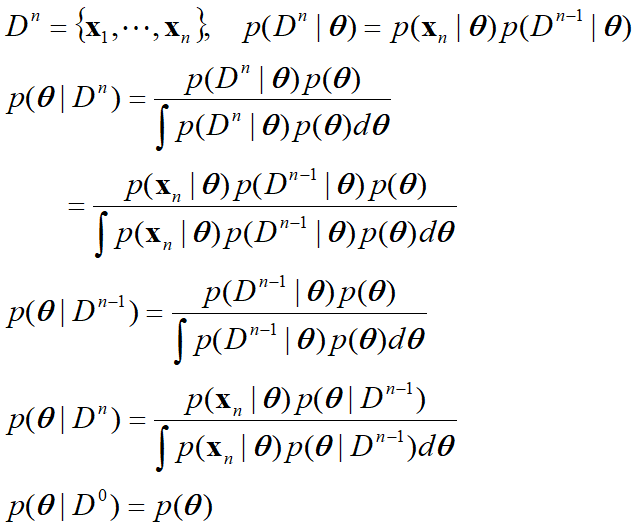
该过程称为参数估计的递归贝叶斯方法，一种增量学习方法。
唯一性问题：
p(x|θ) 是唯一的：后验概率序列 p(θ|Dn) 收敛到 delta 函数；只要训练样本足够多，则 p(x|θ) 能唯
一确定θ。
在某些情况下，不同θ值会产生同一个 p(x|θ) 。p(θ|Dn) 将在 θ 附近产生峰值，这时不管p(x|θ) 是
否唯一， p(x|Dn)总会收敛到p(x) 。因此不确定性客观存在。
最大似然估计和贝叶斯参数估计的区别：
| 最大似然估计 | 贝叶斯参数估计 | |
| 计算复杂度 | 微分 | 多重积分 |
| 可理解性 | 确定易理解 | 不确定不易理解 |
| 先验信息的信任程度 | 不准确 | 准确 |
| 例如 p(x|q) | 与初始假设一致 | 与初始假设不一致 |
这篇关于机器学习---最大似然估计和贝叶斯参数估计的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
