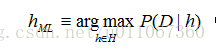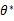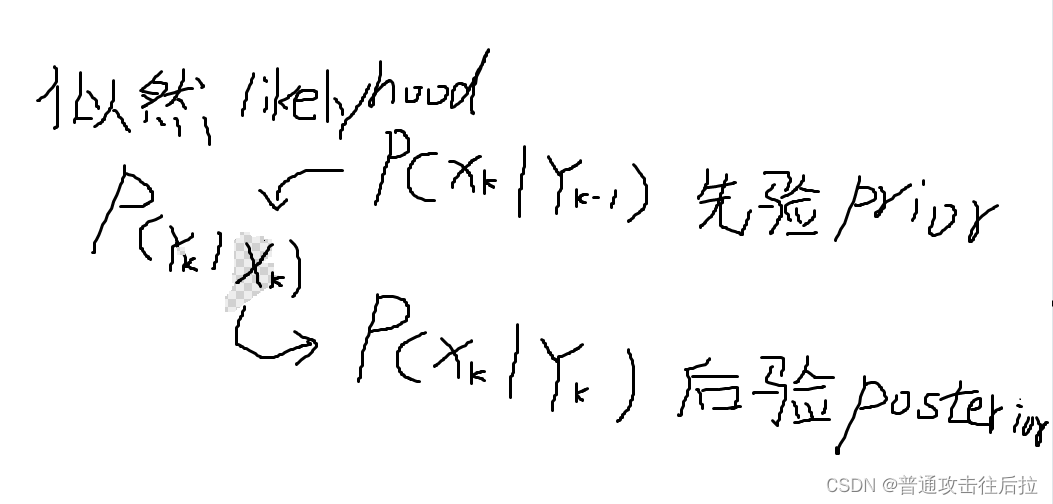似然专题
pytorch负对数似然损失函数介绍
nn.NLLLoss(负对数似然损失)是 PyTorch 中的一种损失函数,常用于分类任务,特别是在模型的输出已经经过了 log-softmax 的情况下。与 nn.CrossEntropyLoss 不同的是,nn.NLLLoss 期望输入的是对数概率值(即 log-softmax 的输出),而不是未经过处理的 logits。 Log-Softmax函数是对Softmax函数的对数版本,它在
损失函数、成本函数cost 、最大似然估计
一、损失函数 什么是损失函数? 【深度学习】一文读懂机器学习常用损失函数(Loss Function)-腾讯云开发者社区-腾讯云 损失函数(loss function)是用来估量模型的预测值f(x)与真实值Y的不一致程度,它是一个非负实值函数,通常使用L(Y, f(x))来表示,损失函数越小,模型的鲁棒性就越好。损失函数是经验风险函数的核心部分,也是结构风险函数重要组成部分。模型的结构风险函
似然概率、先验概率、后验概率和边缘概率
似然概率、先验概率、后验概率和边缘概率是概率论和统计学中的几个重要概念,它们各自具有不同的定义和应用场景。 似然概率 似然概率(Likelihood Probability)或似然函数在统计学中是一种关于统计模型参数的函数。给定输出x时,关于参数θ的似然函数L(θ|x)(在数值上)等于给定参数θ后变量X的概率,即L(θ|x)=P(X=x|θ)。简单来说,似然概率就是当我们有一组数据x时,选择某
熵的相关概念及相互关系(信息熵,条件熵,相对熵,交叉熵,最大似然估计)
熵:系统混乱程度的度量,系统越混乱,熵越大。 信息熵:信息量的大小的度量,用于描述随机变量的不确定度。事件的不确定性越大,则信息量越大,信息熵越大。定义如下: 条件熵:表示在已知随机变量X的条件下随机变量Y的不确定性。定义如下: 另外,,说明描述X和Y所需的信息(H(X,Y)
深入理解交叉熵损失 CrossEntropyLoss - 最大似然估计
深入理解交叉熵损失 CrossEntropyLoss - 最大似然估计 flyfish 下面有详细的例子和公式的说明。 最大似然估计的概念 最大似然估计是一种统计方法,用来估计模型参数,使得在这些参数下观测到的数据出现的概率(即似然)最大。 具体步骤 定义似然函数: 给定一个参数化的概率模型 P ( X ∣ θ ) P(X|\theta) P(X∣θ),其中 θ \theta θ
深入理解交叉熵损失CrossEntropyLoss - 乘积符号在似然函数中的应用
深入理解交叉熵损失CrossEntropyLoss - 乘积符号在似然函数中的应用 flyfish 乘积符号prod,通常写作 ∏ \prod ∏,它类似于求和符号 ∑ \sum ∑,但它表示的是连续乘积。我们来看一下这个符号的具体用法和例子。 乘积符号 ∏ \prod ∏ 乘积符号 ∏ \prod ∏ 用于表示一系列数的乘积。其具体形式如下: ∏ i = 1 n a i \p
数字图像处理成长之路15:前景提取(最大似然估计EM算法与高斯混合模型)
先实践一下何为前景提取: 原始图像 如果画面中有移动的物体,会以白色表现出来。 我理解的前景提取就是把画面中移动的物体提取出来。 这是opencv中给的示意图,来简单看看opencv代码: - 代码 // Global variablesMat frame; //current frameMat fgMaskMOG2; //fg mask fg mask gener
再次思考矩估计与似然估计的原理
再次思考矩估计与似然估计的原理 @(概率论) 首先需要特别强调,矩估计和似然估计都是点估计的具体策略。而点估计强调的是由样本构建一个统计量作为未知参数的估计量。代入具体的观察值就是估计值。 而通常采用的两种方法是: 矩估计法似然估计法 矩估计法的核心是: 对于总体X, EXl=∫+∞−∞xlf(x;θ1,θ2,...,θk)或者离散型:EXl=∑ixliP(X=xi;θ1,
贝叶斯学习--极大后验概率假设和极大似然假设
在机器学习中,通常我们感兴趣的是在给定训练数据D时,确定假设空间H中的最佳假设。 所谓最佳假设,一种办法是把它定义为在给定数据D以及H中不同假设的先验概率的有关知识条件下的最可能(most probable)假设。 贝叶斯理论提供了计算这种可能性的一种直接的方法。更精确地讲,贝叶斯法则提供了一种计算假设概率的方法,它基于假设的先验概率、给定假设下观察到不同数据的概率、以及观察的数据本身。 要
先验概率、后验概率、似然函数的理解
注释:最近一直看到先验后验的说法,一直不懂,这次查了资料记录一下。 1.先验和后验的区别: A.简单的了解两个概率的含义 先验概率可理解为统计概率,后验概率可理解为条件概率。 ---------------------------------------------------------------------------------------------------------
AI学习指南概率论篇-最大似然估计
AI学习指南概率论篇-最大似然估计 概述 在机器学习和人工智能领域中,最大似然估计(Maximum Likelihood Estimation, 简称MLE)是一个重要的概念。它是一种通过观察数据来估计模型参数的方法,通常用来寻找最能解释观测到数据的模型参数值。 最大似然估计在AI中的使用场景 最大似然估计在AI中有着广泛的应用场景,例如在分类算法、回归算法、神经网络等模型中都可以用到
最大似然估计、梯度下降、EM算法、坐标上升
机器学习两个重要的过程:学习得到模型和利用模型进行预测。 下面主要总结对比下这两个过程中用到的一些方法。 一,求解无约束的目标优化问题 这类问题往往出现在求解模型,即参数学习的阶段。 我们已经得到了模型的表达式,不过其中包含了一些未知参数。 我们需要求解参数,使模型在某种性质(目标函数)上最大或最小。 最大似然估计:
最大似然估计(通俗讲解)
最大似然估计 1 最大似然估计(MLE)原理2. 例子2.1 高斯分布2.2 伯努利分布 3. 总结4. 参考 1 最大似然估计(MLE)原理 我们不妨先从名字入手进行理解,最大似然估计的英文名称是 maximum likelihood estimation 即最大可能性估计 它的主要作用是利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。 当“模型已定,参数未
杂记——极大似然估计的渐近正态性
结论 假设 x 1 , ⋯ , x n x_1, \cdots, x_n x1,⋯,xn是来自 f θ ( x ) f_{\theta}(x) fθ(x)的独立同分布样本, θ ^ M L E \hat{\theta}_{MLE} θ^MLE是参数 θ \theta θ的极大似然估计,那么 θ ^ M L E ∼ ˙ N ( θ , 1 n I ( θ ) ) (1) \hat{\t
矩估计和最大似然估计关系
1、矩估计 理论根源是辛钦大数定律,样本之间是独立同分布,当数据样本量很大的时候,样本观测值的平均值和总体的数学期望是在一个极小的误差范围内。 矩估计法, 也称“矩法估计”,就是利用样本矩来估计总体中相应的参数。首先推导涉及感兴趣的参数的总体矩( 即所考虑的随机变量的幂的期望值)的方程。然后取出一个样本并从这个样本估计总体矩。接着使用样本矩取代 (未知的)总体矩,解出感兴趣的参数。从而
LR为什么取log损失函数,又为什么在似然函数计算之后取对数
在学习和做项目的过程中,逐渐加深了对LR的理解。 其中最重要的一点就是为什么取-log函数为损失函数,损失函数的本质就是,如果我们预测对了,能够不惩罚,如果预测错误,会导致损失函数变得很大,也就是惩罚较大,而-log函数在【0,1】之间正好符合这一点,另外还有一点需要说明,LR是一种广义的线性回归模型,平方损失函数的话,对于Sigmoid函数求导计算,无法保证是凸函数,在优化的过程中,求得的解有
贝叶斯公式中的先验概率、后验概率、似然概率
欢迎关注博主 Mindtechnist 或加入【智能科技社区】一起学习和分享Linux、C、C++、Python、Matlab,机器人运动控制、多机器人协作,智能优化算法,滤波估计、多传感器信息融合,机器学习,人工智能等相关领域的知识和技术。关注公粽号 《机器和智能》 回复关键词 “python项目实战” 即可获取美哆商城视频资源! 博主介绍: CSDN博客专家,CSDN优质创作者,CSD
一文搞懂极大似然估计
极大似然估计,通俗理解来说,就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值! 换句话说,极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。 可能有小伙伴就要说了,还是有点抽象呀。我们这样想,一当模型满足某个分布,它的参数值我通过极大似然估计法求出来的话。比如正态分布中公式如下: 如果我通过极大似然估计,得到模型
(八)目标跟踪中参数估计(似然、贝叶斯估计)理论知识
目录 前言 一、统计学基础知识 (一)随机变量 (二)全概率公式 (三)高斯分布及其性质 二、似然是什么? (一)概率和似然 (二)极大似然估计 三、贝叶斯估计 (一)古典统计学与贝叶斯统计学的区别 (二)贝叶斯公式 总结 前言 目标跟踪过程可以看做参数估计的过程,即利用测量信息实时对目标状态进行估计,需要用到很多概率统计的基础知识。在此针对参数估计
《视觉SLAM十四讲》第6讲非线性优化,似然问题P(z,u|x,y)是如何变为最小二乘min J(x,y) (式6-13)的?
最近在学习高翔《视觉SLAM十四讲》中的理论知识,在第六章非线性优化中,解释了为何求解最大概率问题能够转化为最小二乘的优化问题。然而书中有些证明省略掉了,经过请教搞清楚了,特此记在这里。或许能够对其他朋友有帮助。 关键词:如何从求: max P ( z , u ∣ x , y ) \max P(z, u|x, y) maxP(z,u∣x,y) 得到求: min J ( x , y )
机器学习基础--最大似然估计
昨天作报告,讲到机器学习中的基础知识,最大似然估计,老师提了一个问题,就是为什么会写成那个样子,为什么是求argmax,无法回答,于是还是看看概率论吧 机器学习领域,最常用的参数估计准则就是最大似然估计,而且他和我们代价函数最常用的最小均方误差有直接的联系。它的主要思想就是像一位网友说的“眼见为实”。 先说说一个网上的例子,有一个黑箱子里面有100个球,只有黑白两个颜色,一个颜色90个,
先验分布、后验分布、极大似然的一点思考
今天和组里同事聊天的时候,无意中提到了贝叶斯统计里先验分布、后验分布、以及极大似然估计这三个概念。同事专门研究如何利用条件概率做系统辨识的,给我画了一幅图印象非常深刻: 其中k表示时序关系。上面这个图表示后验分布是由先验分布与似然估计一同获得的。 我们经常在代码里给神经网络的最后一层的各个unit的概率值叫likelyhood,其实就是指在当前输入样本下输出各个logit的概率,其含义与极大似
5. 数理统计---极大似然估计
这里写自定义目录标题 5.极大似然估计5.1 似然函数定义5.2 极大似然估计定义5.3 极大似然估计求解的一般过程5.4 极大似然估计的不变性 5.极大似然估计 Fisher的极大似然思想: 随机试验有多个可能结果, 但在一次实验中, 有且只有一个结果会出现. 如果在某次实验中, 结果 ω \omega ω出现了, 则认为该结果(事件{ ω \omega ω})发生的概率 P
基于极大似然算法的系统参数辨识matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 5.完整程序 1.程序功能描述 基于极大似然算法的系统参数辨识。对系统的参数a1,b1,a2,b2分别进行估计,计算估计误差以及估计收敛曲线,然后对比不同信噪比下的估计误差。 2.测试软件版本以及运行结果展示 MATLAB2022a版本运行 3.核心程序
极大似然估计(MLE)和贝叶斯估计(MAP)
极大似然估计(MLE)和贝叶斯估计(MAP) 标签(空格分隔):机器学习笔记 极大似然估计与贝叶斯估计是统计中两种对模型的参数确定的方法,两种参数估计方法使用不同的思想。 前者来自于频率派,认为参数是固定的,我们要做的事情就是根据已经掌握的数据来估计这个参数(上帝眼中参数 θ \theta早已经固定了,带入 xi x_i样本来求 θ \theta,根据样本来求 θ \theta,最大的
概率基础——极大似然估计
概率基础——极大似然估计 引言 极大似然估计(Maximum Likelihood Estimation,简称MLE)是统计学中最常用的参数估计方法之一,它通过最大化样本的似然函数来估计参数值,以使得样本出现的概率最大化。极大似然估计在各个领域都有着广泛的应用,例如机器学习、生物统计学、金融等。本文将介绍极大似然估计的理论基础、公式推导过程,并通过案例和Python代码进行实现和模拟,以帮助读