本文主要是介绍贝叶斯公式中的先验概率、后验概率、似然概率,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

欢迎关注博主 Mindtechnist 或加入【智能科技社区】一起学习和分享Linux、C、C++、Python、Matlab,机器人运动控制、多机器人协作,智能优化算法,滤波估计、多传感器信息融合,机器学习,人工智能等相关领域的知识和技术。关注公粽号 《机器和智能》 回复关键词 “python项目实战” 即可获取美哆商城视频资源!
博主介绍:
CSDN博客专家,CSDN优质创作者,CSDN实力新星,CSDN内容合伙人;
阿里云社区专家博主;
华为云社区云享专家;
51CTO社区入驻博主,掘金社区入驻博主,支付宝社区入驻博主,博客园博主。
贝叶斯公式中的先验概率、后验概率、似然概率
- 贝叶斯公式(bayes)
- 先验概率(prior probability)
- 后验概率(posterior probability)
- 似然概率(likelihood)
专栏:《贝叶斯估计》
贝叶斯公式(bayes)
首先给出贝叶斯(bayes)公式
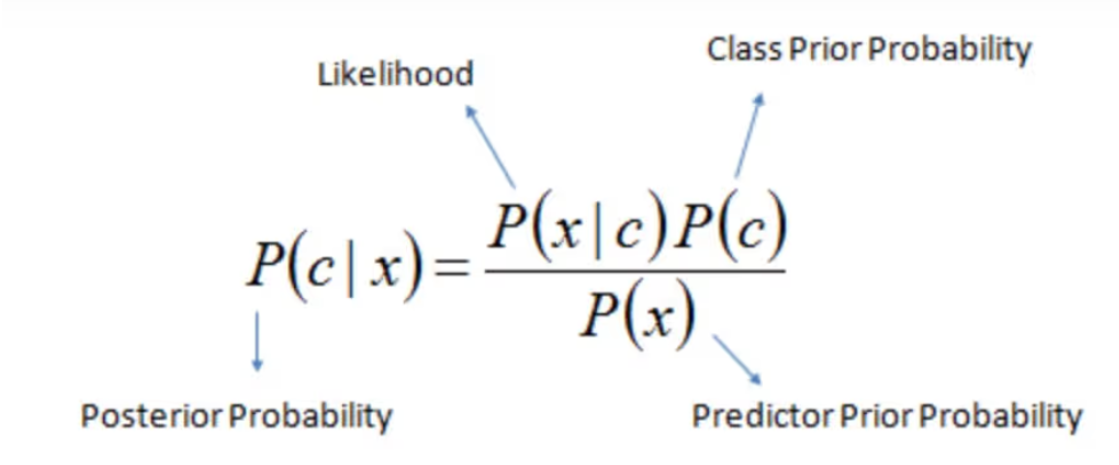
贝叶斯公式为利用搜集到的信息对原有判断进行修正提供了有效手段。
贝叶斯推断的过程通常是这样的:首先,我们有一个未知随机变量的先验分布。然后,我们需要确定观测数据的分布模型,这是一个基于随机变量的条件概率。一旦我们观察到了数据的一个特定值之后,我们就可以开始运用贝叶斯法则去计算随机变量的后验分布。如果是连续型的随机变量,就把上面的概率质量函数替换成概率密度函数就可以了。
贝叶斯方法的核心就是通过先验知识不断更新后验概率密度来分析参数的可能性分布。如果继续进行实验,之前的后验概率密度就变成了先验知识,这样最终就会越来越接近参数的真实分布。需要注意的是,一般来讲如果当前的样本量比先验知识的样本量大很多,那么先验知识就可以忽略不计。另外还有一种先验知识并不是基于早期试验,而是专家意见,这种情况下也可以将其转换为先验概率密度。
先验概率(prior probability)
先验概率(prior probability)是指根据以往经验和分析得到的概率,如全概率公式,它往往作为“由因求果”问题中的“因”出现的概率。在贝叶斯统计中,某一不确定量p的先验概率分布是在考虑“观测数据”前,能表达p不确定性的概率分布。它旨在描述这个不确定量的不确定程度,而不是这个不确定量的随机性。这个不确定量可以是一个参数,或者是一个隐含变量(latent variable)。
也就是说,先验概率是不依靠观测数据的概率分布,也就是与其他因素独立的分布。或者说,先验概率是先于某个事件发生就知道的概率,可以简单理解为经验丰富的专家所进行的纯主观估计(猜测)。以在黑盒中取球为例,假设盒中有9个白球,1个黑球,随机取一个球,拿到的白球的概率是 P(白)=0.9,拿到黑球的概率是 P(黑)0.1,这就是先验概率。
另外,如果利用过去历史资料计算得到的先验概率,称为客观先验概率;如果历史资料无从取得或资料不完全时,凭人们的主观经验来判断而得到的先验概率,称为主观先验概率。 先验概率是通过古典概率模型来定义的,所以也叫做古典概率。古典概率模型要求满足两个条件:试验的所有可能结果是有限的;每一种可能结果出现的可能性(概率)相等。
后验概率(posterior probability)
后验概率(posterior probability)是指在得到“结果”的信息后重新修正的概率,是“执果寻因”问题中的"果"。在贝叶斯统计中,一个随机事件或者一个不确定事件的后验概率是在考虑和给出相关证据或数据后所得到的条件概率。同样,后验概率分布是一个未知量(视为随机变量)基于试验和调查后得到的概率分布。“后验”在本文中代表考虑了被测试事件的相关证据。
也就是说,后验概率是根据贝叶斯(bayes)定理,用先验概率和概率密度函数计算出来的。即”先验概率+观测=后验概率“,通过观测对先验概率更新后即为后验概率。同样以前面提到的黑盒取球为例,后验概率就是在我们已经拿出一个球,以随机变量 x 表示,此时,该球是白球的概率 P(黑|x)就是后验概率。同理,P(黑|观测)和P(白|观测)都是后验概率。
从上面可以看出, 先验概率与后验概率有不可分割的联系,后验概率的计算要以先验概率为基础。事情还没有发生,要求这件事情发生的可能性的大小,是先验概率。事情已经发生,要求这件事情发生的原因是由某个因素引起的可能性的大小,是后验概率。
总结来说,后验概率是在已知”果“的前提下,得到重新修正后的”因“的概率,后验概率也叫做条件概率,可以通过贝叶斯公式来求解。
这里要额外介绍一下最大后验概率(Maximum a posteriori estimation, MAP),最大后验估计是根据经验数据获得对难以观察的量的点估计。与最大似然估计(Maximum likelihood estimation, MLE)类似,但是最大的不同时,最大后验估计的融入了要估计量的先验分布在其中。故最大后验估计可以看做规则化的最大似然估计。
似然概率(likelihood)
在统计学中,似然函数(likelihood function)是一种关于统计模型参数的函数,也称作似然。给定输出 x 时,关于参数 θ 的似然函数 L(θ|x)(在数值上)等于给定参数 θ 后变量 X 的概率: L(θ|x)=P(X=x|θ) 。在数理统计学中,似然函数是一种关于统计模型中的参数的函数,表示模型参数中的似然性(likelihood)。
似然函数在统计推测中发挥重要的作用,因为它是关于统计参数的函数,所以可以用来评估一组统计的参数,也就是说在一组统计方案的参数中,可以用似然函数做筛选。
似然概率其实很好理解,就是说我们现在有一堆数据,现在需要构建一组参数对这些数据建模,以使得模型能够尽可能地拟合这些数据。所以我们要做的就是从很多组参数中选出一组使得模型对数据的拟合程度最高,所以也常常说最大似然概率。
注意“似然”与“概率”意思相近,都是指某种事件发生的可能性,在非正式的语境下,“似然”会和“概率”混着用。但是严格区分的话,在统计上,二者是不同的。不同就在于,观察值 x 与参数 θ 的不同的角色。概率是用于描述一个函数,这个函数是在给定参数值的情况下的关于观察值的函数。而似然是用于在给定一个观察值时,关于用于描述参数的情况。在统计学中,“似然”和“概率”有着明确的区分:“概率”描述了给定模型参数后,描述结果的合理性,而不涉及任何观察到的数据;“似然”描述了给定了特定观测值后,描述模型参数是否合理。比如说抛掷硬币,我们抛掷一枚”均匀“的硬币,总共抛10,有五次为正面的可能性就是概率;如果已经抛了10次,其中5次为正面,那么这枚硬币”均匀“的可能性就是似然。
这里不得不提一下统计学中的两大学派了
频率派:频率派认为样本信息来自总体,通过对样本信息的研究可以合理地推断和估计总体信息。频率派的核心思想是基于大样本理论,将概率看作频率的极限,以样本观测值的频率为基础进行推断。频率派注重数据的重复抽样和统计量的性质,比如点估计、置信区间和假设检验等。频率派认为参数是客观存在的,不会改变,虽然未知,但却是固定值。最典型的便是极大似然估计(MLE)。
贝叶斯派:贝叶斯派认为任何一个未知量都可以看作是随机的,应该用一个概率分布去描述未知参数,而不是频率派认为的固定值。贝叶斯派的核心思想是先验信息与后验信息相结合,通过贝叶斯公式将先验信息与样本数据进行结合,得到后验分布,并以此作为对未知参数的推断。贝叶斯派强调主观先验信息的引入,因此不同人可能会有不同的先验分布,从而导致不同的推断结果。贝叶斯派注重个体的主观判断和背景信息,更加灵活和主观。最典型的便是最大后验估计(MAP)。


这篇关于贝叶斯公式中的先验概率、后验概率、似然概率的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








