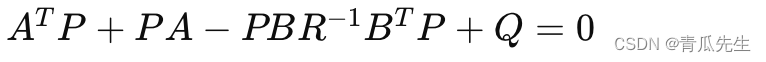二次专题
一些数学经验总结——关于将原一元二次函数增加一些限制条件后最优结果的对比（主要针对公平关切相关的建模）
1.没有分段的情况 原函数为一元二次凹函数（开口向下），如下： 因为要使得其存在正解，必须满足，那么。 上述函数的最优结果为：，。 对应的mathematica代码如下： Clear["Global`*"]f0[x_, a_, b_, c_, d_] := (a*x - b)*(d - c*x);(*(b c+a d)/(2 a c)*)Maximize[{f0[x, a, b,
【线性代数】正定矩阵，二次型函数
本文主要介绍正定矩阵，二次型函数，及其相关的解析证明过程和各个过程的可视化几何解释（深蓝色字体）。 非常喜欢清华大学张颢老师说过的一段话：如果你不能用可视化的方式看到事情的结果，那么你就很难对这个事情有认知，认知就是直觉，解析的东西可以让你理解，但未必能让你形成直觉，因为他太反直觉了。 正定矩阵 定义 给定一个大小为 n×n 的实对称矩阵 A ，若对于任意长度为 n 的非零向量 ，有 恒成
async-http-android框架的介绍和二次封装
1。先谈谈框架吧 相信大家一看，就应该想到是一款异步请求的框架了，也就是说他的网络请求是在非UI线程中执行的，而callback在创建他的线程中，应用了Handler的机制。 项目本生的官方网址：http://loopj.com/android-async-http/， 对应的github地址： https://github.com/loopj/android-async-http
Spark Sql 二次分组排序取TopK
基本需求 用spark sql求出每个院系每个班每个专业前3名 样本数据 数据格式：id,studentId,language,math,english,classId,departmentId，即id，学号，语文，数学，外语，班级，院系 1,111,68,69,90,1班,经济系2,112,73,80,96,1班,经济系3,113,90,74,75,1班,经济系4,
C1-2 ABB二次SDK开发——手把手教登录对应的机器人控制器（图片引导操作）登录机器人控制器和刷新机器人列表
1.完成配置后我们开始进行操作 C1-1 ABB二次SDK开发——C#Window窗体-环境配置（带ABB二次开发SDK资源包）-CSDN博客文章浏览阅读95次。3.记住路径，右键C#引用，然后导入ABB.Robotics.Controllers.PC.dll。2.安装资源文件PCABB二次开发的SDK，并打开安装路径。1.新建VSC#的windowfrom项目。4.在框架代码主界面代码中添加。
最优化方法Python计算：一般凸二次规划的有效集算法
先考虑仅含不等式约束的二次规划 { minimize 1 2 x ⊤ H x + c ⊤ x s.t. A x ≥ b . ( 1 ) \begin{cases} \text{minimize}\quad \frac{1}{2}\boldsymbol{x}^\top\boldsymbol{Hx}+\boldsymbol{c}^\top\boldsymbol{x}\\ \text{s.t.\
最优化方法Python计算：二次规划的拉格朗日算法
目标函数为二次式，约束条件为线性式的最优化问题称为二次规划。其一般形式为 { minimize 1 2 x ⊤ H x + c ⊤ x s.t. A e q x − b e q = o A i q x − b i q ≥ o . \begin{cases} \text{minimize}\quad \frac{1}{2}\boldsymbol{x}^\top\boldsymbol{Hx}+\
C1-1 ABB二次SDK开发——C#Window窗体-环境配置（带ABB二次开发SDK资源包）
一.使用Visual Stdio创建一个项目 1.新建VSC#的windowfrom项目 2.安装资源文件PCABB二次开发的SDK，并打开安装路径 3.记住路径，右键C#引用，然后导入ABB.Robotics.Controllers.PC.dll 4.在框架代码主界面代码中添加 using ABB.Robotics.Controllers;using ABB.Roboti
YoloV10改进策略：卷积篇|基于PConv的二次创新|附结构图|性能和精度得到大幅度提高（独家原创）
文章目录 摘要论文指导PConv在论文中的描述改进YoloV10的描述 改进代码与结构图改进方法测试结果总结 摘要 在PConv的基础上做了二次创新，创新后的模型不仅在精度和速度上有了质的提升，还可以支持Stride为2的降采样。 改进方法简单高效，需要发论文的同学不要错过！ 论文指导 PConv在论文中的描述 论文： 下面我们展示了可以通过利用特征图的冗余来进一步优化成本
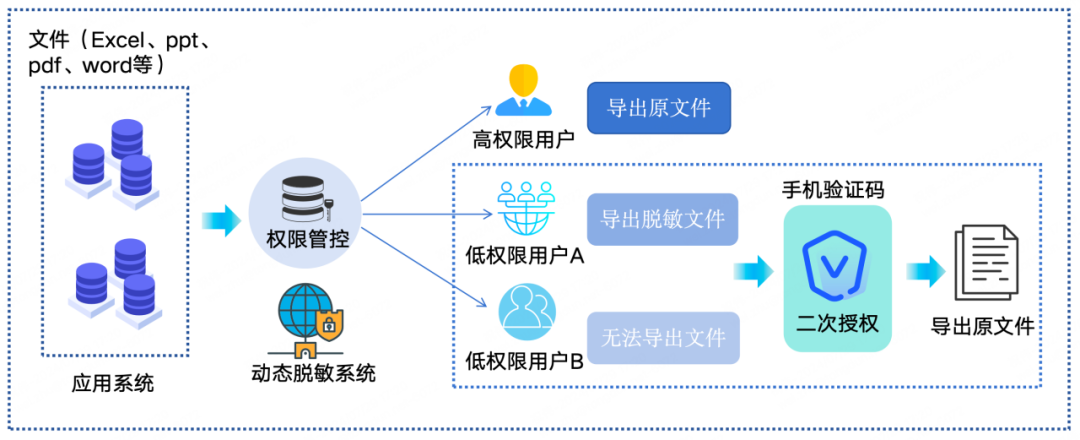
极盾故事|某金融租赁机构应用数据保护新策略：“动态脱敏”“二次授权”
数据的流通使用是创新的动力，但安全和合规是不可逾越的底线。企业如何在这三者之间找到平衡点？ 极盾科技，助力某金融租赁机构，基于极盾·觅踪构建应用数据动态脱敏系统，实现10＋核心应用系统的统一管理，对个人金融信息5大要素（姓名、身份证、手机号、银行卡、地址）基于用户身份实现差异化动态脱敏，并结合“二次授权”策略实现敏感数据访问和文件导出的控制，以满足更多场景的不同需求。 01 数据可用与
《西瓜书》第六章 公式6.6 凸二次规划问题
1. 凸优化问题 对于一般的非线性规划，若目标函数是凸函数，约束集合 D D D 是凸集，则称该非线性规划是凸规划。 若上述约束规划中只含有不等式约束，又 c i ( x ) ( i ∈ I ) c_i(x)(i∈I) ci(x)(i∈I)是凸函数，则约束集 D D D 是凸集。 对于混合约束问题，若 c i ( x ) ( i ∈ E ) c_i(x)(i∈E) ci(x)(i∈E
Python优化算法20——精英反向学习与二次插值改进的黏菌算法(ISMA)
科研里面优化算法都用的多，尤其是各种动物园里面的智能仿生优化算法，但是目前都是MATLAB的代码多，python几乎没有什么包，这次把优化算法系列的代码都从底层手写开始。 需要看以前的优化算法文章可以参考：Python优化算法_阡之尘埃的博客-CSDN博客 算法背景 之前写过黏菌优化算法的文章，现在有很多新的黏菌优化算法，都是进行了一些改进。本次带来的是混沌精英黏菌算法，当然也会和普
Vue3 进阶教程：一文详解 el-table 组件的二次封装技巧！
开发后台管理系统，在业务上接触的最多就是表单（输入）和表格（输出）了。对于使用 Vue 框架进行开发的同学来说，组件库 Element 是肯定会接触的，而其中的 el-table 和 el-form 更是管理系统中的常客。 然而，一旦项目的表格或表单多起来，每个不同的配置，以及多一个字段少一个字段，都要在 template 中重新写一大段组件代码，显得非常麻烦。或许你会考虑将这些代码封装起来，可
HDU5734(二次函数最值)
题目链接 把题目的公式展开后，就是二次函数，然后在对称轴取到最小值 ymin = n*a-a*a/n #include<bits/stdc++.h>using namespace std;#define cl(a,b) memset(a,b,sizeof(a))#define LL long long#define gcd __gcdconst int maxn = 1e4+200;
二次封装useEffect hook,实现页面加载时不触发
首先对useEffect进行二次封装 import { useEffect, useRef } from 'react';type Callback = () => void;function useEffectWithInitialEffect(callback: Callback,deps: React.DependencyList,shouldRunOnInitialRender: boo
笔记整理—uboot启动过程（3）栈的二次设置以及常用名词解析，BL1部分完
前文说到了uboot的lowlevel_init都干了些什么，也就是经过了这项初期的低级启动，使得我们能在串口监视器上看见机器打印出的第一句话“OK”。当lowlevel_init结束后，uboot去做了另一件事情，那就是栈的再次设置。 第一次栈设置发生在lowlevel_init之前，在SRAM中设置的栈，现在要做的是将栈移动到DDR中。（ARM 是满减栈）
c++的二次分发与访问者模式
c++/java/c#等面向对象的编程语言，都是单次分发，有些场景下单次分发已经不能满足要求，因此可以借助访问者设计模式完成二次分发设计： // VisitAccept.h#pragma onceclass Acceptor;class Visitor{public:virtual void visit(Acceptor* acp);};class Visitor1 :public
公共筛选组件（二次封装antd）支持代码提示
如果项目是基于antd组件库为基础搭建，可使用此公共筛选组件 使用到的库 npm i antdnpm i lodash-esnpm i @types/lodash-es -D /components/CommonSearch index.tsx import React from 'react';import { Button, Card, Form } from 'antd'
自动驾驶规划中使用 OSQP 进行二次规划 代码原理详细解读
目录 1 问题描述 什么是稀疏矩阵 CSC 形式 QP Path Planning 问题 1. Cost function 1.1 The first term: 1.2 The second term: 1.3 The thrid term: 1.4 The forth term: 对 Qx''' 矩阵公式的验证 整体 Q 矩阵（就是 P 矩阵，二次项的权重矩阵）
智能优化算法改进策略之局部搜索算子(三)—二次插值法
1、原理介绍 多项式是逼近函数的一种常用工具。在寻求函数极小点的区间（即寻查区间）上，我们可以利用在若干点处的函数值来构成低次插值多项式，用它作为求极小点的函数的近似表达式，并用这个多项式的极小点作为原函数极小点的近似。低次多项式的极小点比较容易计算。常用的插值多项式为二次或三次，一般说来三次插值公式的收敛性好一些，但在导数不变计算时，三点二次插值也是一种常用的方法[1]。 3
《图数据库：理论与实践》书籍销售火爆，二次印刷重磅来袭！
好书共享，就在此刻！ 由创邻科技联合电子工业出版社匠心打磨三年，最终成稿的图数据库书籍《图数据库：理论与实践》发行上线后，获得了广泛好评，各平台销量迅速破千，并荣登京东 “数据库图书榜”热卖榜第二名。 基于广大读者的强烈需求和市场的持续认可，电子工业出版社迅速决定对书籍进行二次印刷，让更多的软件开发人员、数据分析师、图技术爱好者能够了解图技术，学习图技术、用好图技术！ 为什么选择《图数据库
二次规划（Lagrange 方法，起作用集方法）
二次规划是非线性规划中一种特殊情形，它的目标函数是二次实函数，约束是线性的。由于二次规划比较简单，便于求解，且一些非线性规划可以转化为求解一系列二次规划问题，因此二次规划算法较早引起人们的重视，成为求解非线性规划的一个重要通径。二次规划的算法较多，本章介绍其中几个典型的方法，它们是 Lagrange 方法，起作用集方法，Lemke 方法和路径路踪法。 一、Lagrange 方法 考虑二次规划问
线性二次型调节器（LQR）举例
线性二次型调节器（LQR） 线性二次型调节器（LQR）是一种用于最优控制的问题，其中目标是通过最小化某个代价函数来找到最优控制策略。LQR特别适用于线性系统。为了在人形机器人上应用LQR进行建模，主要步骤包括建立系统模型、定义代价函数以及求解最优控制律。以下是详细步骤： 1. 系统建模 首先，建立人形机器人的线性状态空间模型。一般形式如下： 其中，x(t) 是状态向量，u(t) 是控制向量
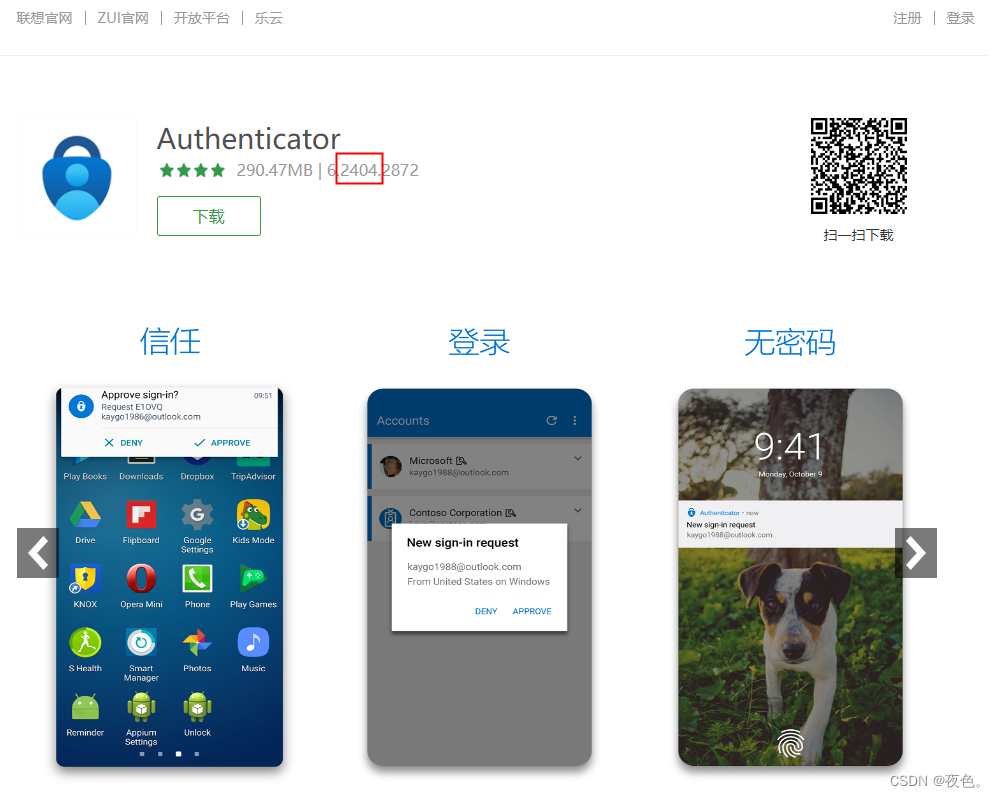
GitHub强制双重验证、二次验证之下载微软Authenticator
Download Microsoft Authenticator 如上图，安卓手机在国内，基本没有下载使用的可能。 下载 Microsoft Authenticator 如上图，找到了国内下载渠道，但仅联想商店的新版本适合使用，下载安装即可。
曲线拟合 | 二次B样条拟合曲线
B 样条曲线拟合实例：能平滑化曲线 1. 实例1 为MASS包中mcycle数据集。它测试了一系列模拟的交通车事故中，头部的加速度，以此来评估头盔的性能。times为撞击时间(ms)，accel为加速度（g）。首先导入数据，并绘制散点图 (1) 关键函数 # bs() ====# bs(x, df = NULL, knots = NULL, degree = 3, intercep
【线性代数】第七章-二次型
文章目录 一. 基本内容与重要结论1. 二次型、二次型矩阵2. 标准型与规范型3. 惯性指数4. 坐标变换5. 矩阵合同6. 正定矩阵与正定二次型 二. 主要定理1. 二次型的坐标变换2. 任意二次型都可变换为标准型3. 实对称矩阵总可以合同一个对角矩阵4. 惯性定理5. 实对称矩阵总可以化成标准形6. 二次型正定的充要条件 二次型的两大板块要复习整理清楚，一个是标准形，另一个是