本文主要是介绍智能优化算法改进策略之局部搜索算子(三)—二次插值法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1、原理介绍
多项式是逼近函数的一种常用工具。在寻求函数极小点的区间(即寻查区间)上,我们可以利用在若干点处的函数值来构成低次插值多项式,用它作为求极小点的函数的近似表达式,并用这个多项式的极小点作为原函数极小点的近似。低次多项式的极小点比较容易计算。常用的插值多项式为二次或三次,一般说来三次插值公式的收敛性好一些,但在导数不变计算时,三点二次插值也是一种常用的方法[1]。


3、仿真实验
以海洋捕食者算法(MPA)为基本算法。考察基于二次插值法的改进海洋捕食者算法(命名为QIMPA) vs. 海洋捕食者算法(MPA)
在Sphere函数上:
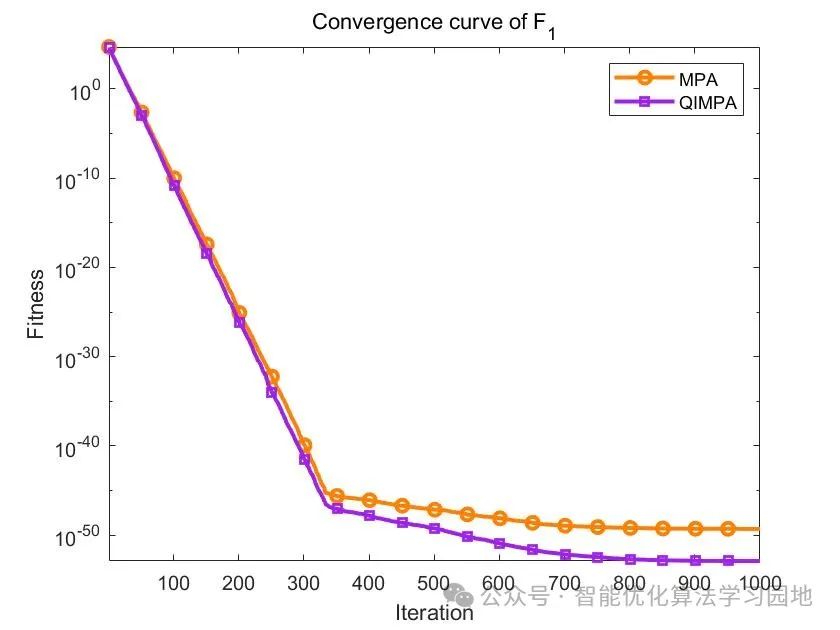
在Schwefel's2.21上:

在CEC2017-5上:
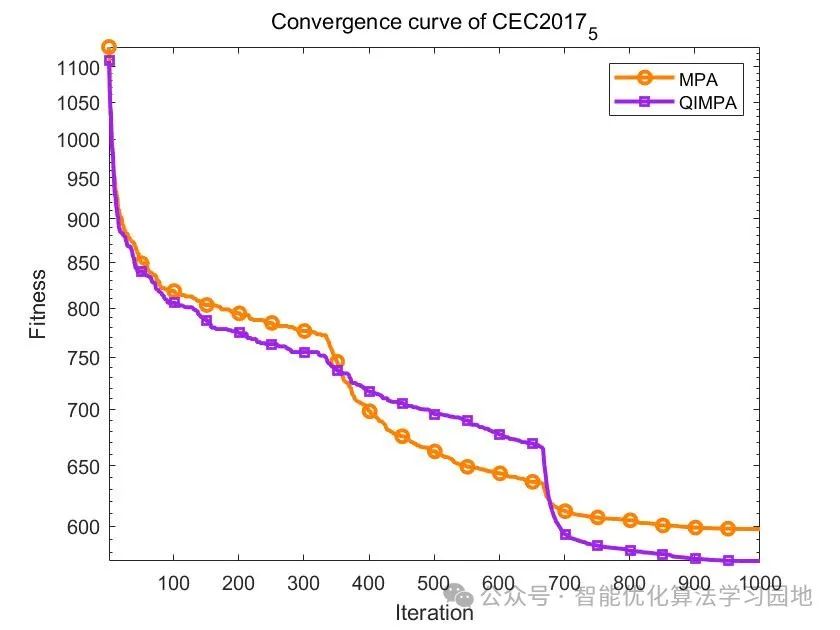
在CEC2017-8上:

在CEC2017-12上:

代码获取:

4、参考文献
[1] Sun W, Yuan Y X. Optimization theory and methods: nonlinear programming[M]. Springer Science & Business Media, 2006.
这篇关于智能优化算法改进策略之局部搜索算子(三)—二次插值法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





