插值法专题
计算方法——插值法程序实现(一)
例题 给出的函数关系表,分别利用线性插值及二次插值计算的近似值。 0.10.20.30.40.51.1051711.2214031.3498591.4918251.648721 参考代码一:Python代码实现(自编码) import math""":parameter用于计算插值多项式的系数"""def Parameters(data_x,data_y,size):param
智能优化算法改进策略之局部搜索算子(三)—二次插值法
1、原理介绍 多项式是逼近函数的一种常用工具。在寻求函数极小点的区间(即寻查区间)上,我们可以利用在若干点处的函数值来构成低次插值多项式,用它作为求极小点的函数的近似表达式,并用这个多项式的极小点作为原函数极小点的近似。低次多项式的极小点比较容易计算。常用的插值多项式为二次或三次,一般说来三次插值公式的收敛性好一些,但在导数不变计算时,三点二次插值也是一种常用的方法[1]。 3
自然数幂和 拉格朗日插值法和第二类斯特林数法
写在这里,目的是在以后需要看的时候不用再去网上抄(划掉) 求 s ( n ) = ∑ i = 1 n i k 求s(n)=\sum_{i=1}^n i^k 求s(n)=i=1∑nik 拉格朗日插值法 给定若干个点值,(x0,y0),(x1,y1),(xn,yn),它们的差值多项式 L ( x ) = ∑ i = 0 n y i ∗ ∏ j ≠ i x − x j x i − x j L(
拉格朗日插值法 C语言实现
/* *作者:KDF5000 *功能:利用拉格朗日插值法求解近似值 *时间:2013.4.15 */ #include <stdio.h> #include <stdlib.h> #include <string.h> //存放插值节点 struct Data{ double x; double y; struct Data *
【图像边缘检测】基于matlab插值法亚像素边缘检测【含Matlab源码 306期】
⛄一、获取代码方式 获取代码方式1: 完整代码已上传我的资源: 【图像边缘检测】基于matlab插值法亚像素边缘检测【含Matlab源码 306期】 (https://download.csdn.net/download/TIQCmatlab/62925370) 点击上面蓝色字体,直接付费下载,即可。 获取代码方式2: 付费专栏Matlab图像处理(初级版) 备注: 点击上面蓝色字体付费专栏
双三次插值法(Bicubic interpolation)
双三次插值法(Bicubic interpolation)相对前两种算法计算过程更为复杂,考虑了待求像素坐标反变换后得到的浮点坐标周围的16个邻近像素。目的坐标M(x,y)和浮点坐标m(i+u,j+v),需要选取插值基函数来拟合数据,最常用的插值基函数是对sin[(πx)/x]的逼近。计算公式 function re_im = dthird(im, p, q)%双三次插值法实现图像缩放,输入
双线性插值法(Bilinear interpolation)
双线性插值法(Bilinear interpolation)是利用待求象素反变换到原图像对应的浮点坐标,邻近的四个象素在两个方向上作线性内插。四邻近像素值的加权平均即为待测点像素值,计算权重反比于浮点在双线性方向上的映射距离。双线性插值是利用了需要处理的原始图像浮点坐标周围的四个像素点的相关性,通过双线性算法计算。同上A中所设,目的坐标M(x,y)和浮点坐标m(i+u,j+v),则: f(M
图像旋转算法双线性插值法详解
双线性插值法是一种常用的插值算法,用于在图像旋转、缩放等操作中估计目标像素的灰度值。它基于近邻像素之间的灰度变化趋势进行推断,从而提供更平滑和精确的结果。 双线性插值算法的基本思想如下: 首先,根据旋转角度确定旋转中心(通常为图像的中心)。然后计算旋转后的图像尺寸,保证不丢失原始图像的任何信息。 对于旋转后的每一个像素位置,根据逆时针旋转方向,将目标图像坐标映射回原图像坐标。 根据目标图
拉格朗日插值法——matlab代码实现
公式: function y=lagrange(x0,y0,x)% 给定一系列点x0,y0 % x是我们要预测的值,由于可以有多个,因此用向量表示% y返回我们的估计值,由于可以有多个,因此用向量表示n = length(x);% 要预测的个数y = zeros(n);% 初始化,并赋初值0for k = 1:length(x0)j_no_k=find((1:length(x0))~=k
HRV去伪影:通过比较当前的RR值与周围10个RR间隔值(medRR)的中位数,可以检测到缺失或额外的节拍,采用的是中位数插值,并不是三样条插值法
java趣味算法:获取数组中第i个值并且周围十个数的中位数 前言提取部分算法:思路 前言 经调研发现,国内外基于脉搏波收集的RRI数据容易产生伪差,受到运动干扰较大,夜间睡眠、静息状态下的数据可能质量相对更好。因为人体交感和副交感神经调节的昼夜节律,白天和夜间静息下的HRV指标也会有波动。所以从Huawei Research直接拿到的数据是会存在一定的伪影数据,不能直接用于计算。
Matlab解决简单4次牛顿差值,Matlab插值法
实验目的: 1.Matlab中多项式的表示及多项式运算 2.用Matlab实现拉格朗日及牛顿插值法 3.用多项式插值法拟合数据 实验要求: 1.掌握多项式的表示和运算 2.拉格朗日插值法的实现(参见吕同富版教材) 3.牛顿插值法的实现(参见吕同富版教材) 实验内容: 1.多项式的表达式和创建;多项式的四则运算、导数与积分。 2.用Matlab实现拉格朗日及牛顿插值法。 3.用多项式插值法拟合数据
布伦特方法(Brent‘s method)---结合二分法、割线法和逆二次插值法的求根方法
基础介绍: 给定给定区间,函数连续且,那么根据介值定理,函数必然在区间内有根。 二分法:将区间不断二分,使端点不断逼近零点。下一次迭代的区间为或,其中。割线法(线性插值):基本思想是用弦的斜率近似代替目标函数的切线斜率,并用割线与横轴交点的横坐标作为方程式的根的近似。即给定两个点,。其割线方程为,那么令,x的值即为下一次迭代的结果。逆二次插值法:为割线法的进化版本。使用三个点确定一个二次函数,
(20200331)双线性插值法(C语言)
参考: 【1】https://blog.csdn.net/sinat_32602421/article/details/98940243 //双线性插值//20200331#define _CRT_SECURE_NO_WARNINGS#include <stdio.h>#include <stdlib.h>#include <math.h>double my_bilinear(dou
拉格朗日插值法-Python
#利用拉格朗日法进行插补import pandas as pd #导入数据分析库Pandasfrom scipy.interpolate import lagrange #导入拉格朗日插值函数 inputfile = 'G:/py/data/data.xls' #销量数据路径outputfile = 'G:/py/tmp/data2.xls' #输出数据路径 data = pd.rea
数学建模之插值法及代码
发现更多知识,欢迎访问Cr不是铬的个人网站 引言 数模比赛中,常常需要根据已知的函数点进行数据、模型的处理和分析,而有时候现有的数据是极少的,不足以支撑分析的进行,这时就需要使用一些数学的方法,“模拟产生”一些新的但又比较靠谱的值来满 足需求,这就是插值的作用。 插值法的定义 插值法的原理 拉格朗日插值法 说在前面,在数学建模比赛中,拉格朗日插值不好,有龙格现象。 不
拉格朗日c语言实验报告,拉格朗日(Lagrange)插值法(C语言)
题目 拉格朗日插值法流程图 (1)二次插值: #include float lagelangri(float x[],float y[],float xx,int n) { int i,j; float *a,yy=0; a=new float[n]; for(i=0;i<=n-1;i++) { a[i]=y[i]; for(j=0;j<=n-1;j++) if(j!=i)a[i]*=(xx
Newton插值法 | matlab实现
function y_p = Newton(x, y, x_p)% x为插值节点的横坐标% y为插值节点的纵坐标% x_p 为需计算的插值函数值的横坐标% y_p 为插值函数值i = length(x) - 1;iter = 1;num = length(x_p);y_i = y(1);y_p = [];%for n = 1: numdif_quo = []; % 存放差商whi
Newton插值法 | 差商 + Newton插值公式 + 插值余项
Newton插值法 Aitken逐次插值法虽然具有承袭性的特点,但其插值公式是递推型的,不便于进行理论分析。为此,可以把n次插值多项式改写成升幂的形式: N n ( x ) = c 0 + c 1 ( x − x 0 ) + c 2 ( x − x ) ( x − x 1 ) + ⋯ + c n ( x − x 0 ) ( x − x 1 ) ⋯ ( x − x n − 1 ) (10) N_
Aitken(埃特金)逐次插值法 | 一次插值、二次插值、k次插值
Aitken(埃特金)逐次插值法 判断离散数据 ( x i , y i ) ( i = 0 , 1 , 2 , ⋯ , n ) (x_i,y_i)(i=0,1,2,\cdots,n) (xi,yi)(i=0,1,2,⋯,n)的插值精度,既可以采用事后误差估计的方法,也可以在插值点x的附近选取部分数据进行插值,然后再增加一些插值节点进行插值。若两次的插值结果之差小于规定的误差,则可认为插值精度
【数值分析】2 - 插值法
文章目录 一、引言1.1 插值法引入1.2 常用插值法1.3 插值法定义 二、插值法研究的问题2.1 插值多项式存在的唯一性2.2 如何构造n次多项式2.2.1 待定系数法2.2.2 拉格朗日插值法2.2.2.1 拉格朗日多项式2.2.2.2 拉格朗日插值余项2.2.2.3 例题2.2.2.4 拉格朗日插值法的问题 2.2.3 牛顿插值法2.2.3.1 牛顿插值思想2.2.3.2 差商的定义
【Python】用Python绘制折线图(插值法平滑曲线)
目录 利用绘制图表:matplotlib官网 1. 小试牛刀——柱状图 1.1 matplotlib库默认英文字体 2. 折线图绘制 2.1 读取exal方法 2.1.1 数据处理常用库:pandas 2.1.2 找到pandas在pathon安装的位置Lib->site-package 2.2 提取列表数组 3. 论文图片的类型和格式 4. Python绘制折线
RBF(Radial-Basis Function)网路之一:多元插值法
1 插值:在离散数学的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点。(来自百度百科)插值除了给定的离散数据点外,连续曲线的其他点都属于“插入”进来的,所以称插值。 在多维空间的插值法定义为: 给定N个不同的点集和一组相对应的N个实数集合,找到一个函数满足如下的条件:
Lagrange插值法实验:求拉格朗日插值多项式和对应x的近似值matlab实现(内附代码)
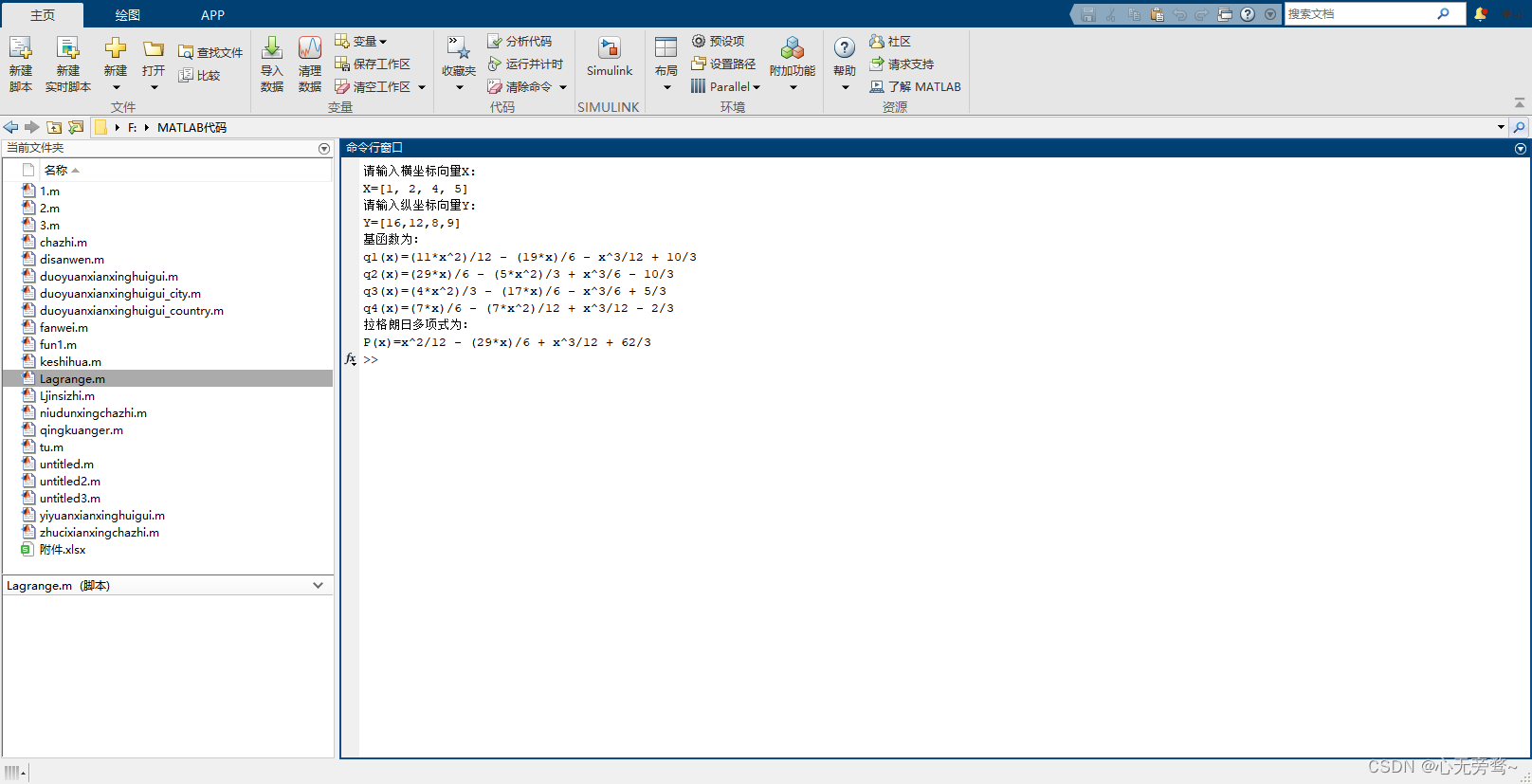
一、实验要求 已知函数表: 求出Lagrange 插值多项式,并计算x=1.2处的y的近似值。 二、MATLAB代码 求解多项式: X = input('请输入横坐标向量X:\nX='); % 获取用户输入的横坐标向量Y = input('请输入纵坐标向量Y:\nY='); % 获取用户输入的纵坐标向量m = length(X); % 获取节点个数L = ones(m, m)
Lagrange插值法实验:求拉格朗日插值多项式和对应x的近似值matlab实现(内附代码)
一、实验要求 已知函数表: 求出Lagrange 插值多项式,并计算x=1.2处的y的近似值。 二、MATLAB代码 求解多项式: X = input('请输入横坐标向量X:\nX='); % 获取用户输入的横坐标向量Y = input('请输入纵坐标向量Y:\nY='); % 获取用户输入的纵坐标向量m = length(X); % 获取节点个数L = ones(m, m)