本文主要是介绍线性二次型调节器(LQR)举例,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
线性二次型调节器(LQR)
线性二次型调节器(LQR)是一种用于最优控制的问题,其中目标是通过最小化某个代价函数来找到最优控制策略。LQR特别适用于线性系统。为了在人形机器人上应用LQR进行建模,主要步骤包括建立系统模型、定义代价函数以及求解最优控制律。以下是详细步骤:
1. 系统建模
首先,建立人形机器人的线性状态空间模型。一般形式如下:
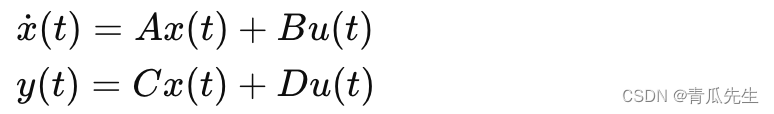
其中,x(t) 是状态向量,u(t) 是控制向量,A 是系统矩阵,B 是输入矩阵,C 是输出矩阵,D 是直接传输矩阵。
2. 定义代价函数
LQR的目标是最小化以下二次型代价函数:

3. 求解Riccati方程
为了找到最优控制律,需要求解Riccati方程:
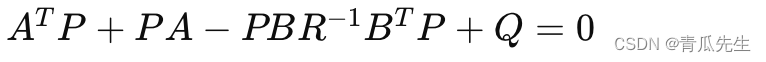
通过求解此方程可以得到矩阵 P。
4. 最优控制律
最优控制律为:
这篇关于线性二次型调节器(LQR)举例的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






