lqr专题
【自动驾驶】控制算法(五)连续方程离散化与离散LQR原理
写在前面: 🌟 欢迎光临 清流君 的博客小天地,这里是我分享技术与心得的温馨角落。📝 个人主页:清流君_CSDN博客,期待与您一同探索 移动机器人 领域的无限可能。 🔍 本文系 清流君 原创之作,荣幸在CSDN首发🐒 若您觉得内容有价值,还请评论告知一声,以便更多人受益。 转载请注明出处,尊重原创,从我做起。 👍 点赞、评论、收藏,三连走一波,让我们一起养成好习惯😜 在这里,您将
线性二次型调节器(LQR)举例
线性二次型调节器(LQR) 线性二次型调节器(LQR)是一种用于最优控制的问题,其中目标是通过最小化某个代价函数来找到最优控制策略。LQR特别适用于线性系统。为了在人形机器人上应用LQR进行建模,主要步骤包括建立系统模型、定义代价函数以及求解最优控制律。以下是详细步骤: 1. 系统建模 首先,建立人形机器人的线性状态空间模型。一般形式如下: 其中,x(t) 是状态向量,u(t) 是控制向量
基于LQR控制算法的电磁减振控制系统simulink建模与仿真
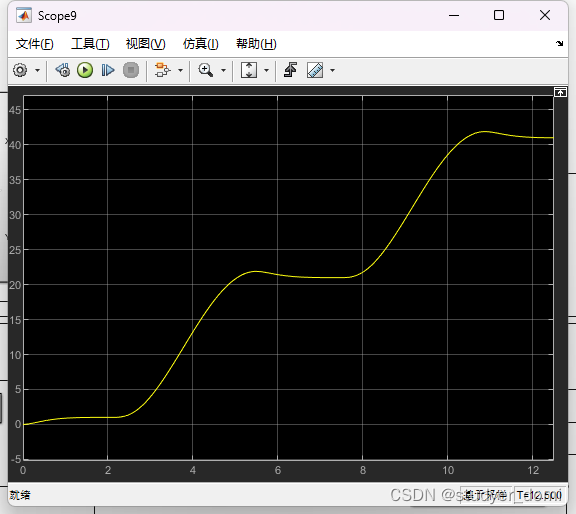
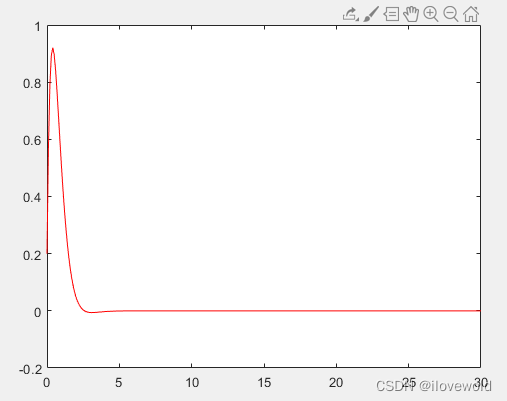
目录 1.课题概述 2.系统仿真结果 3.核心程序与模型 4.系统原理简介 5.完整工程文件 1.课题概述 基于LQR控制算法的电磁减振控制系统simulink建模与仿真。仿真输出控制器的收敛曲线。 2.系统仿真结果 3.核心程序与模型 版本:MATLAB2022a 08_029m 4.系统原理简介 电磁减振控制系统采用线性二次型调节器
车辆运动模型中LQR代码实现
一、前言 最近看到关于架构和算法两者关系的一个描述,我觉得非常认同,分享给大家。 1、好架构起到两个作用:合理的分解功能、合理的适配算法; 2、好的架构是好的功能的必要条件,不是充分条件,一味追求架构的完美是不可取的,并且不存在完美的架构,只存在合适的架构; 3、好的架构可以一定层度上提升算法的能力,但功能开发不能将重心全放在框架上,应该追求框架+算法的适配,从而实现 1+1 > 2 。 *
差速机器人模型LQR 控制仿真(c++ opencv显示)
1 差速机器人状态方程构建 1.1差速机器人运动学模型 1.2模型线性化 1.3模型离散化 2离散LQR迭代计算 注意1:P值的初值为Q。见链接中的: 注意2:Q, R参数调节 注意3:LQR一般只做横向控制,不做纵向控制。LQR输出的速度为速度差,需要进一步转换 3点镇定路径跟踪 通过调整参考路径,实现分段LQR路径跟踪: ①先旋转; ②直线跟踪到目标点; ③
机器人控制系统中LQG与LQR
LQG控制,也被称为线性二次高斯问题的最优控制,是随机控制理论中对具有高斯噪声的随机线性系统使二次性能指标取最小值的一类控制。LQG控制是对确定性情形的LQ问题的最优控制(见极大值原理)相对于随机情形的推广,具有良好的结构性质(中性、分离性、确定性等价)。 LQR(线性二次型调节器)则是一种基于状态反馈的最优控制策略。其原理主要包括确定状态方程模型、线性化处理、定义目标函数以及优化目标函数等步骤
轨迹规划 | 图解最优控制LQR算法(附ROS C++/Python/Matlab仿真)
目录 0 专栏介绍1 最优控制理论2 线性二次型问题3 LQR的价值迭代推导4 基于差速模型的LQR控制5 仿真实现5.1 ROS C++实现5.2 Python实现5.3 Matlab实现 0 专栏介绍 🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(
学习下控制 LQR加上观测器
这里主要参考B站上的,DR_CAN,极力推荐看下,这里主要是结合观测器和LQR的设计。在观测器基础上引入LQR 这里的Y的C=[1 0],可知X1输出是可以用实际值的,可以不用的X1hat
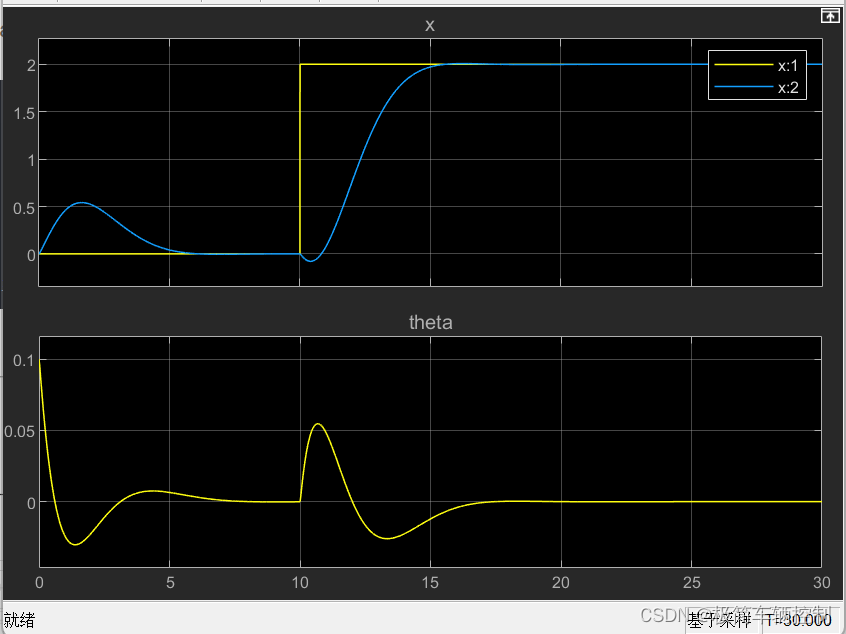
小车倒立摆系统极点配置,LQR闭环控制
在之前直流电机控制仿真里有讲过状态控制的基本架构,有兴趣的同学可以再回去看看,链接如下好玩的直流电机调速实验、PID、极点配置、LQR、观测器;不讲大道理_lqr控制器观测器-CSDN博客 在专栏的前三篇文章 小车倒立摆物理建模与simulink仿真-CSDN博客 小车倒立摆系统线性化,离散化处理-CSDN博客 小车倒立摆系统能控和能观性分析-CSDN博客 我们建立的小车的状态空间方
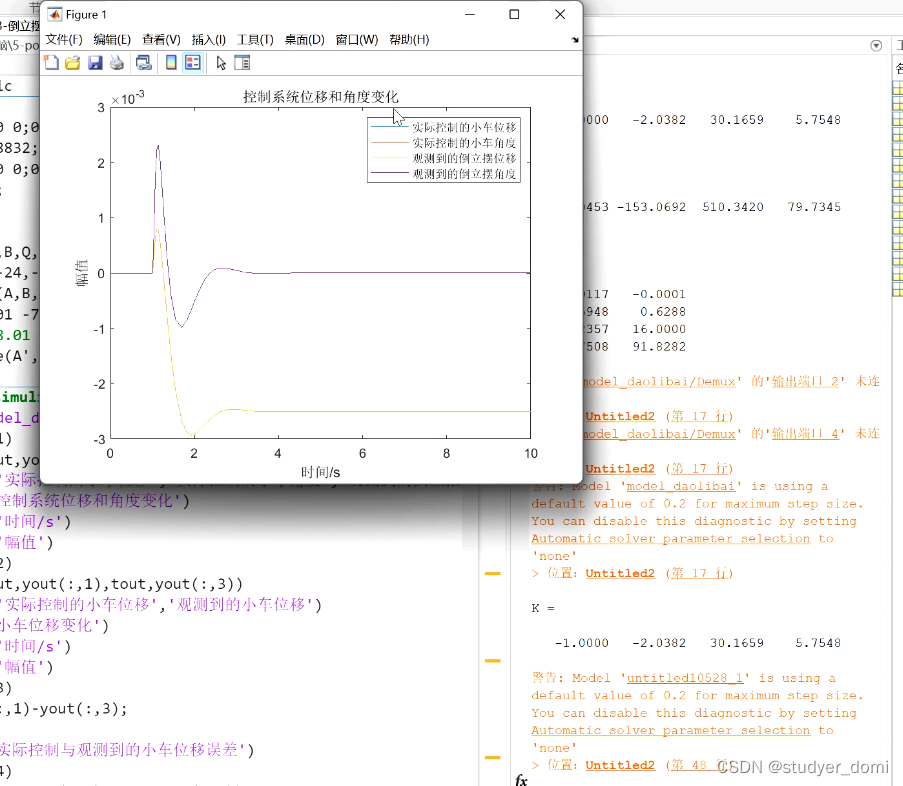
matlab simulink 一阶倒立摆LQR控制
1、内容简介 略 80-可以交流、咨询、答疑 一阶倒立摆LQR控制 2、内容说明 略 一级倒立摆系统的数学模型 系统的组成系统由小 车、小球和轻质杆组成。 倒摆通过转动关节安装在 驱动小车上,杆子的一端 固定在小车上,另一端可 以自由的左右倒下。通过 对小车施加一定的外部驱 动力,使倒摆保持一定的 姿势。 小车质量 ;
Constrained Iterative LQR 自动驾驶中使用的经典控制算法
Motion planning 运动规划在自动驾驶领域是一个比较有挑战的部分。它既要接受来自上层的行为理解和决策的输出,也要考虑一个包含道路结构和感知所检测到的所有障碍物状态的动态世界模型。最终生成一个满足安全性和可行性约束并且具有理想驾驶体验的轨迹。 通常,motion planners中对collision avoidance的约束的表示比较复杂。因为为了处理具有高度动态的驾驶交互场景流,需
无人机|LQR控制算法及其无人机控制中的应用仿真
前言 LQR全称Linear Quadratic Regulator(线性二次调节器),顾名思义用于解决形如 x ˙ = A x + B u y = C x + D u \begin{aligned}\dot{x}&=Ax+Bu\\y&=Cx+Du\end{aligned} x˙y=Ax+Bu=Cx+Du 线性时不变系统的一种线性控制方法,是最优控制方法的一种。 LQR通过全状态反馈将不同
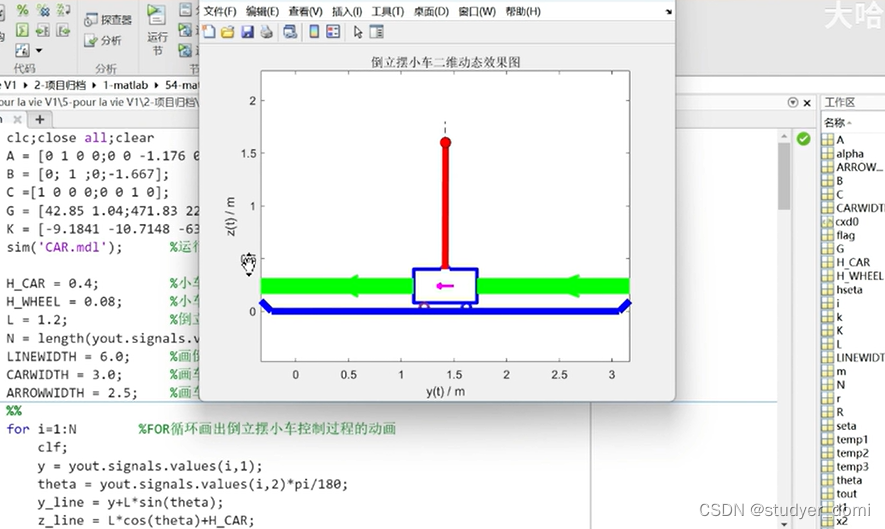
matlab倒立摆小车LQR控制动画
1、内容简介 略 54-可以交流、咨询、答疑 2、内容说明 略 摆杆长度为 L,质量为 m 的单级倒立摆(摆杆的质心在杆的中心处),小车的质量为 M。在水平方向施加控制力 u,相对参考系产生位移为 y。为了简化问题并且保其实质不变,忽略执行电机的惯性以及摆轴、轮轴、轮与接触面之间的摩擦力及风力。 3、仿真分析 略 matlab倒立摆小车LQR控制动画_哔
无人驾驶控制算法LQR和MPC的仿真实现
1. LQR控制器 1.1 问题陈述 考虑一个质量为 m m m 的滑块在光滑的一维地面上运动。初始时,滑块的位置和速度均为 0 0 0。我们的目标是设计一个控制器,基于传感器测得的滑块位置 x x x,为滑块提供外力 u u u,使其能够跟随参考点 x r x_r xr 运动。 为建立动力学模型,我们采用以下微分方程: x ¨ = u m \ddot x = \frac
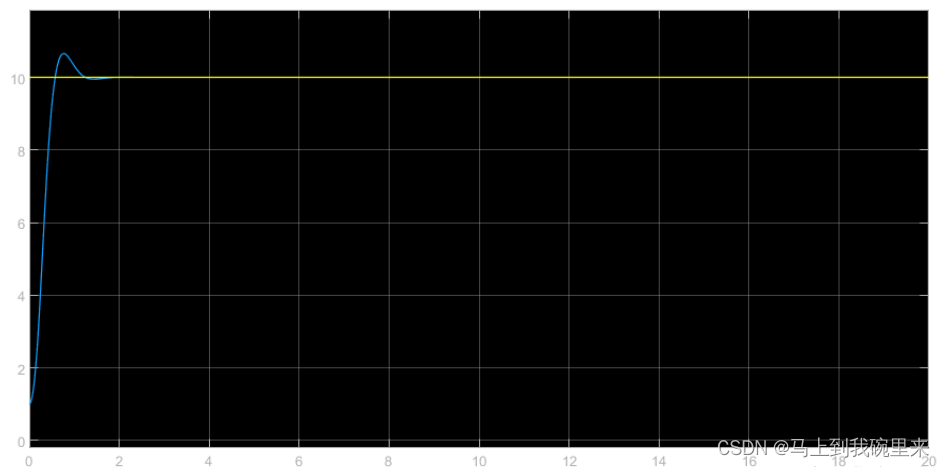
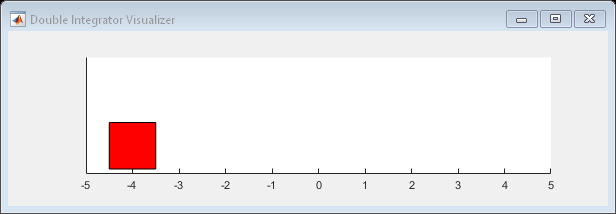
MATLAB - 比较 DDPG Agent 和 LQR 控制器
系列文章目录 前言 本示例展示了如何训练深度确定性策略梯度(DDPG)Agent,以控制 MATLAB® 中建模的二阶线性动态系统。该示例还将 DDPG Agent 与 LQR 控制器进行了比较。 有关 DDPG 代理的更多信息,请参阅深度确定性策略梯度 (DDPG) 代理。有关如何在 Simulink® 中训练 DDPG agent 的示例,请参阅训练 DDPG agent 向上摆
[足式机器人]Part2 Dr. CAN学习笔记-Advanced控制理论 Ch04-7 LQR控制器 Linear Quadratic Regulator
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记-Advanced控制理论 Ch04-7 LQR控制器 Linear Quadratic Regulator 线性控制器设计-轨迹跟踪(Fellow a Desired Path)
matlab基于线性二次调节器(LQR)法实现机器人路径规划可变轨迹跟踪
1、内容简介 略 可以交流、咨询、答疑 2、内容说明 基于线性二次调节器(LQR)法实现机器人路径规划可变轨迹跟踪 3、仿真分析 略 load path.mat%% 轨迹处理% 定义参考轨迹refPos_x = path(:,1);refPos_y = path(:,2);refPos = [refPos_x, refPos_y];% 计算航向角和曲率diff_x =
基于LQR算法跟踪圆形轨迹,MATLAB 代码
希望做一个分享者 轨迹跟踪效果图 位姿误差图 参考博文 LQR 的直观推导及简单应用_白巧克力亦唯心的博客-CSDN博客_lqr算法 关键词:泰勒展开;黎卡提方程求解;状态反馈 clear all;close all;clc;%% 参数ts=0.1;t=30;d=1.45;%% 初始状态x(1)=0;y(1)=0;xita(1)=0;v=3;w=
基于Matlab simulink的自动驾驶车道保持adas辅助模型,后续会继续此模型更新,把pid换成LQR或者MPC
基于Matlab simulink的自动驾驶车道保持adas辅助模型,后续会继续此模型更新,把pid换成LQR或者MPC。 需要的自取,可以为模型 需要版本Matlab2021a YID:9249665214165236

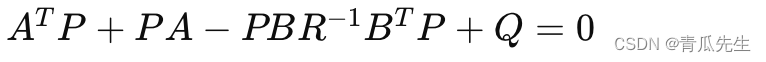






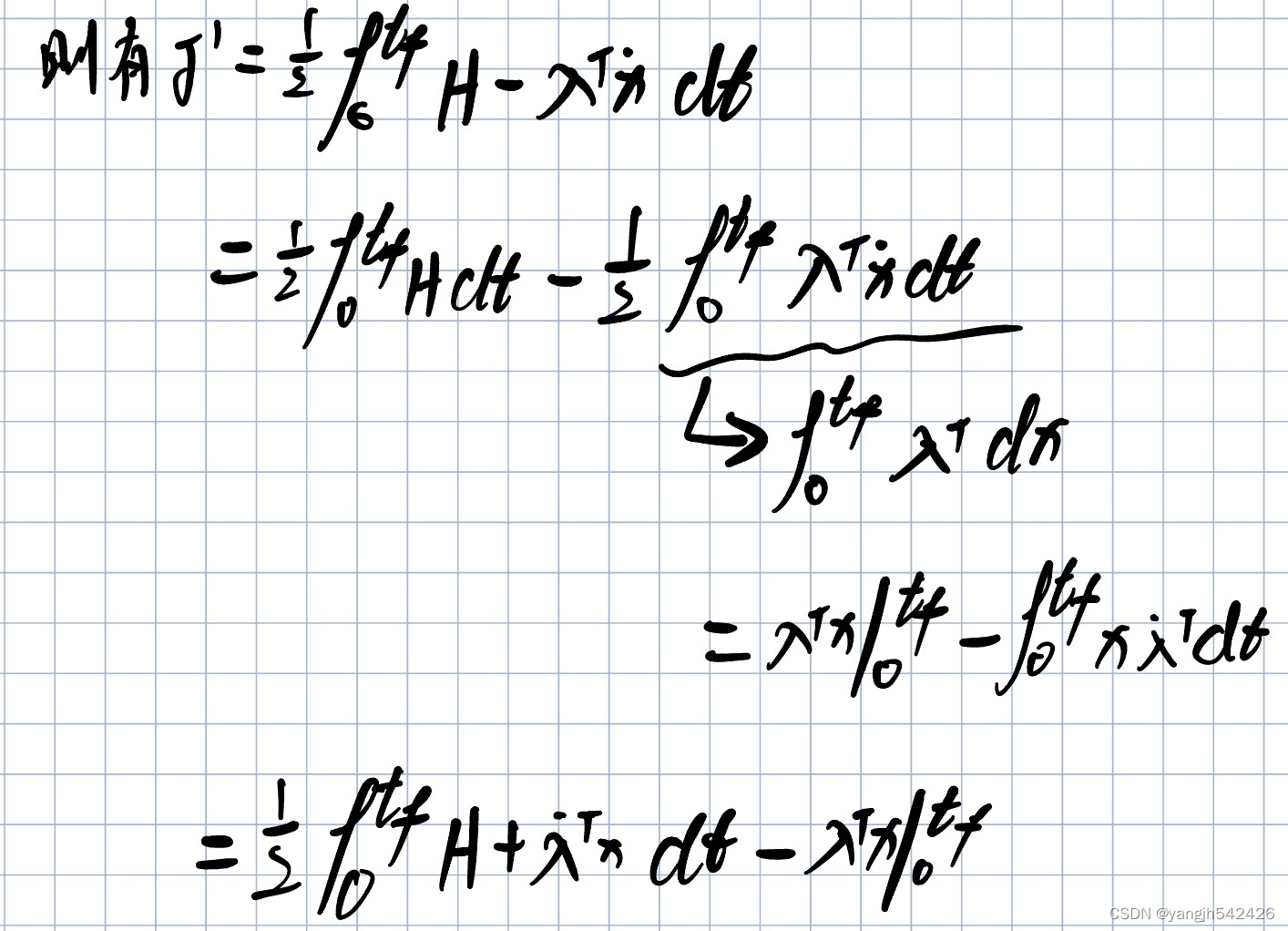
![[足式机器人]Part2 Dr. CAN学习笔记-Advanced控制理论 Ch04-7 LQR控制器 Linear Quadratic Regulator](https://img-blog.csdnimg.cn/direct/10eaecbbeb514e9995a5ccaee8562098.png#pic_center)