基于LQR算法跟踪圆形轨迹，MATLAB 代码

希望做一个分享者

轨迹跟踪效果图

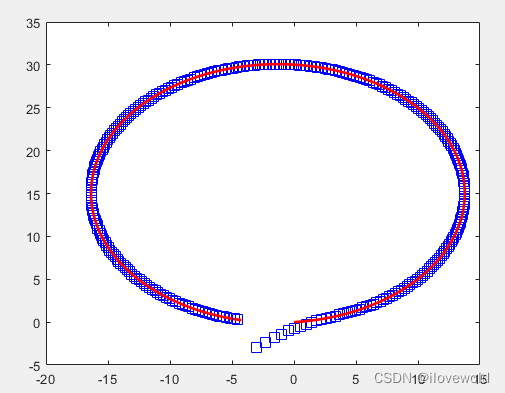
位姿误差图

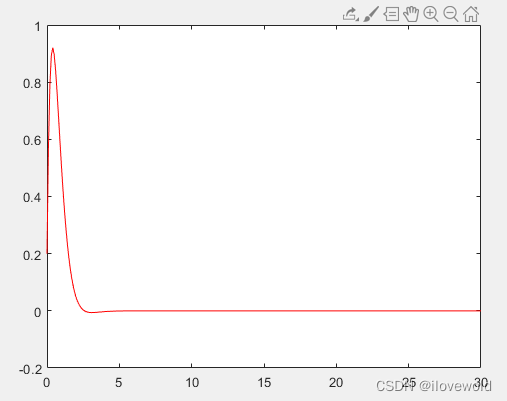
参考博文

LQR 的直观推导及简单应用_白巧克力亦唯心的博客-CSDN博客_lqr算法

关键词：泰勒展开；黎卡提方程求解；状态反馈

clear all;
close all;
clc;%% 参数
ts=0.1;
t=30;
d=1.45;%% 初始状态
x(1)=0;
y(1)=0;
xita(1)=0;
v=3;
w=0.2;
u=[v;w];
Z(:,1)=[-3;-3;0.2];
for k=1:1:t/tstimes(k+1)=k*ts;X(:,k)=[cos(xita(k)) -d*sin(xita(k));sin(xita(k)) d*cos(xita(k));0 1]*u;%% 状态更新x(k+1)=x(k)+X(1,k)*ts;y(k+1)=y(k)+X(2,k)*ts;xita(k+1)=xita(k)+X(3,k)*ts;A=[0 0 -v*sin(xita(k))-d*w*cos(xita(k));0 0 v*cos(xita(k))-d*w*sin(xita(k));0 0 0];B=[cos(xita(k)) -d*sin(xita(k));sin(xita(k)) d*cos(xita(k));0 1];Q=[2 0 0;0 2 0;0 0 2];R=[1 0; 0 1];K=lqr(A,B,Q,R);Z_=(A-B*K)*Z(:,k);%每秒变化率Z(:,k+1)=Z(:,k)+Z_*ts;%每步变化率xc(k)=Z(1,k)+x(k);yc(k)=Z(2,k)+y(k);
endfigure(1)
for k=1:1:length(xc)
plot(x,y,'r','Linewidth',2);
hold on;
plot(xc(k),yc(k),'sb','MarkerSize',10);
pause(0.1);
end
figure(2)
plot(times,Z(1,:),'r');
figure(3)
plot(times,Z(2,:),'r');
figure(4);
plot(times,Z(3,:),'r');