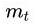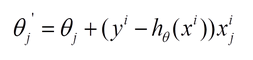sgd专题

AI学习指南深度学习篇-SGD的变种算法

AI学习指南深度学习篇 - SGD的变种算法深度学习是人工智能领域中最为重要的一个分支，而在深度学习的训练过程中，优化算法起着至关重要的作用。随机梯度下降（SGD，Stochastic Gradient Descent）是最基本的优化算法之一。然而，纯SGD在训练深度神经网络时可能会面临收敛速度慢和陷入局部最优的问题。因此，许多变种SGD算法应运而生，极大地提高了模型的训练效率和效果。本文

AI学习指南深度学习篇-随机梯度下降法（Stochastic Gradient Descent，SGD）简介

AI学习指南深度学习篇-随机梯度下降法（Stochastic Gradient Descent，SGD）简介在深度学习领域，优化算法是至关重要的一部分。其中，随机梯度下降法（Stochastic Gradient Descent，SGD）是最为常用且有效的优化算法之一。本篇将介绍SGD的背景和在深度学习中的重要性，解释SGD相对于传统梯度下降法的优势和适用场景，并提供详细的示例说明。 1.

【ShuQiHere】SGD vs BGD：搞清楚它们的区别和适用场景

【ShuQiHere】在机器学习中，优化模型是构建准确预测模型的关键步骤。优化算法帮助我们调整模型的参数，使其更好地拟合训练数据，减少预测误差。在众多优化算法中，梯度下降法是一种最为常见且有效的手段。梯度下降法主要有两种变体：批量梯度下降（Batch Gradient Descent, BGD）和随机梯度下降（Stochastic Gradient Descent, SGD）。这两者

SGD，Momentum，AdaGrad，RMSProp，Adam等优化算法发展历程

各种优化算法层出不穷，看的眼花缭乱，如果不能理清楚其中他们的关系及发展历程，必然会记得很混乱及模糊最开始做神经网络的时候大家更新参数的时候都是把所有数据计算一遍，求所以数据的平均梯度再进行参数调节，后来觉得这样太慢了，干脆就计算一条数据就调节一次，这就叫随机梯度下降了（SGD），随机两字的由来是因为每条数据可能调节的方向都不一样，下降的过程会很震荡。这都是两个极

Scaling SGD Batch Size to 32K for ImageNet Training

为了充分利用GPU计算,加快训练速度,通常采取的方法是增大batch size.然而增大batch size的同时,又要保证精度不下降,目前的state of the art 方法是等比例与batch size增加学习率,并采Sqrt Scaling Rule,Linear Scaling Rule,Warmup Schem等策略来更新学来率. 在训练过程中,通过控制学习率,便可以在训练的时候采

随机梯度下降（SGD）

随机梯度下降（SGD）随机梯度下降（Stochastic Gradient Descent，SGD）是一种用于优化机器学习模型的基本算法。SGD通过迭代地调整模型参数，使损失函数达到最小，从而优化模型性能。它是深度学习中最常用的优化算法之一，尤其适用于大规模数据集和高维度参数空间。 SGD的基本思想 SGD的核心思想是通过每次仅使用一个样本或一小部分样本（称为mini-batch）来估计梯

随机梯度下降SGD的理解和现象分析

Pytorch常用的函数(八)常见优化器SGD,Adagrad,RMSprop,Adam,AdamW总结

Pytorch常用的函数(八)常见优化器SGD,Adagrad,RMSprop,Adam,AdamW总结在深度学习中，优化器的目标是通过调整模型的参数，最小化（或最大化）一个损失函数。优化器使用梯度下降等迭代方法来更新模型的参数，以使损失函数达到最优或接近最优。如下图，优化算法可分为一阶算法和二阶算法，常用的是一阶算法，今天主要介绍下一阶优化相关的优化器。 1 SGD优化

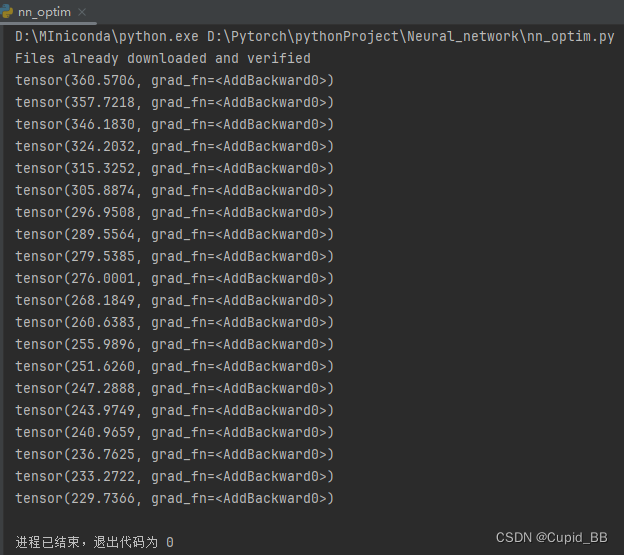
torch.optim的灵活使用(包括重写SGD，加上L1正则)

torch.optim的灵活使用 1. 基本用法：要构建一个优化器Optimizer，必须给它一个包含参数的迭代器来优化，然后，我们可以指定特定的优化选项，例如学习速率，重量衰减值等。注：如果要把model放在GPU中，需要在构建一个Optimizer之前就执行model.cuda()，确保优化器里面的参数也是在GPU中。例子： optimizer = optim.SGD(mod

PyTorch的十个优化器（SGD，ASGD，Rprop，Adagrad，Adadelta，RMSprop，Adam(AMSGrad)，Adamax，SparseAdam，LBFGS）

本文截取自《PyTorch 模型训练实用教程》，获取全文pdf请点击：https://github.com/tensor-yu/PyTorch_Tutorial 文章目录 1 torch.optim.SGD 2 torch.optim.ASGD 3 torch.optim.Rprop 4 torch.optim.Adagrad 5 torch.optim.Adadelta 6 torch.op

Mxnet (27): 小批量随机梯度下降（Minibatch-SGD）

目前为止，梯度学习的方法中有两个极端：一次使用所有的数据计算梯度和更新参数；一次计算一次梯度。 1 向量化和缓存决定使用小批量的主要原因是计算效率。当考虑并行化到多个GPU和多个服务器时很好解释。我们需要向每一个GPU至少发送一个图像，假设每个服务器8个GPU一共16个服务器，那么我们的最小批次已经达到了128。在单个GPU甚至CPU来看，情况更加微妙。设备的内存类型千奇百怪，用于计算

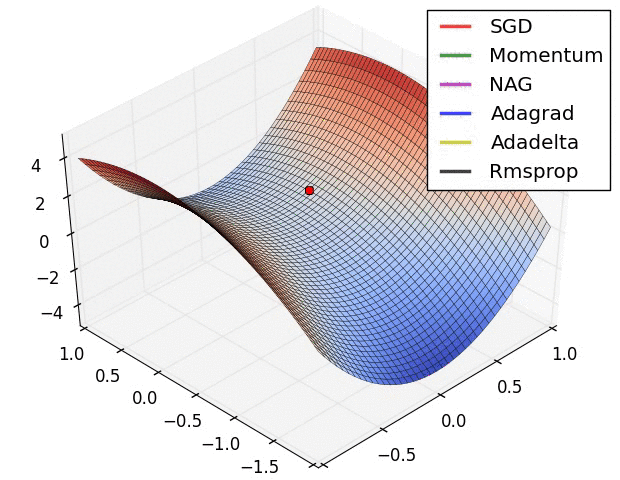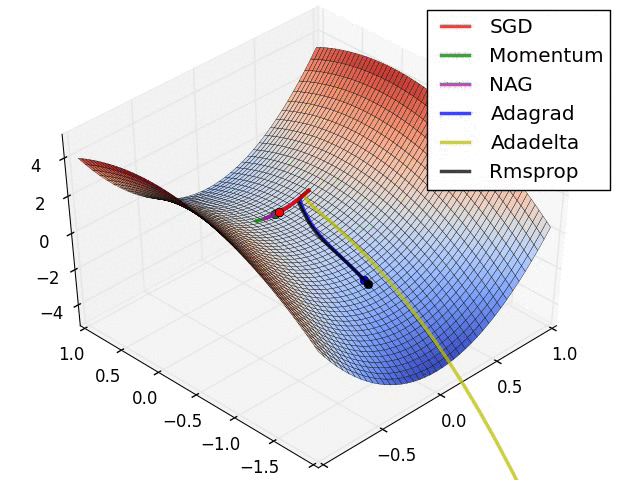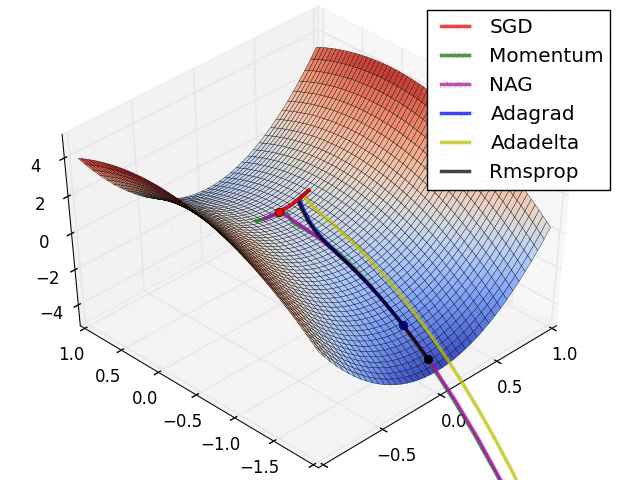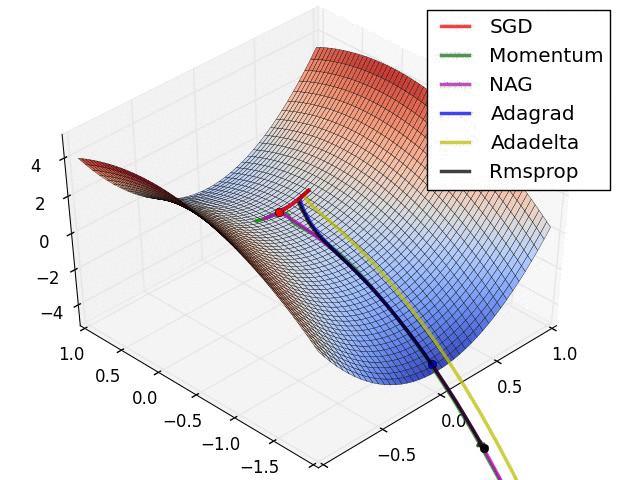
sgd Momentum Vanilla SGD RMSprop adam等优化算法在寻找简单logistic分类中的的应用

参考博文 (4条消息) sgd Momentum Vanilla SGD RMSprop adam等优化算法在寻找函数最值的应用_tcuuuqladvvmm454的博客-CSDN博客在这里随机选择一些数据生成两类核心代码如下： def __init__(self, loss,

sgd Momentum Vanilla SGD RMSprop adam等优化算法在寻找函数最值的应用

1\sgd q=q-a*gt a是学习率 gt是函数的梯度也就是沿着梯度的反方向得到下降最快的，最快能找到函数的最值 2 Momentum 然后q=q-mt 3 RMSprop 4 Adam Adam[6] 可以认为是 RMSprop 和 Momentum 的结合。和 RMSprop 对二阶动量使用指数移动平均类似，Adam 中对一阶动量也是用指

转载的损失函数MSE L1 优化函数ADAM SGD 优化算法等

如有侵权，请联系删除！ pytorch框架中损失函数与优化器介绍：目录 1. 损失函数： 1.1　nn.L1Loss 1.2　nn.SmoothL1Loss 1.3　nn.MSELoss 1.4　nn.BCELoss 1.5　nn.CrossEntropyLoss 1.6　nn.NLLLoss 1.7　nn.NLLLoss2d 2.优化器Optim 2.1 使用 2

Adagrad求sqrt SGD Momentum Adagrad Adam AdamW RMSProp LAMB Lion 推导

随机梯度下降（Stochastic Gradient Descent）SGD 经典的梯度下降法每次对模型参数更新时，需要遍历所有的训练数据。随机梯度下降法用单个训练样本的损失来近似平均损失。 θ t + 1 = θ t − η g t ( 公式 1 ) \theta_{t+1} = \theta_{t}-\eta g_t (公式1) θt+1=θt−ηgt(公式1) 小批量梯度下降法（

torch.optim.SGD 和 torch.optim.Adam的区别？

目录 torch.optim.SGD优点缺点适合的场景 torch.optim.Adam优点缺点适合的场景 Adam优化器和SGD（随机梯度下降）优化器是深度学习中常用的两种优化算法，它们在优化模型参数方面有一些区别。 torch.optim.SGD SGD优化器是基于随机梯度下降的算法，它以每个样本的梯度为基准来更新模型的参数。优点计算简单，对大规模数据集可扩展性强

自适应学习速率SGD优化方法比较（SGD，Adagrad，Adadelta，Adam，Adamax，Nadam）

深度学习最全优化方法总结比较（SGD，Adagrad，Adadelta，Adam，Adamax，Nadam）前言（标题不能再中二了）本文仅对一些常见的优化方法进行直观介绍和简单的比较，各种优化方法的详细内容及公式只好去认真啃论文了，在此我就不赘述了。 SGD 此处的SGD指mini-batch gradient descent，关于batch gradient desc

GraphSAIL 贝叶斯公式 epoch batch iteration区别 GD与SGD 一些代码问题

目录 2021.05.25 看论文GraphSAIL2021.05.26 写论文2021.05.27 论文注意点题目摘要本机安装包 2021.07.02 论文审稿回顾代码贝叶斯公式2021.07.05函数epoch batch iteration 2021.07.06GD和SGD 2021.07.072021.07.132021.07.18看论文随手记英文 2021.08.02

各类优化方法总结（从SGD到FTRL）

目录目录各类优化方法总结 1. SGD2. Momentum3. Nesterov4. Adagrad5. Adadelta6. Adam7. FTRL 参考资料各类优化方法总结为了方便描述，假设第 t t t轮要更新的某参数是wtwtw_t， loss l o s s loss函数关于 wt w t w_t的偏导数表示为 gt g t g_t，即：

深度学习笔记（六）——网络优化（2）：参数更新优化器SGD、SGDM、AdaGrad、RMSProp、Adam

文中程序以Tensorflow-2.6.0为例部分概念包含笔者个人理解，如有遗漏或错误，欢迎评论或私信指正。截图和程序部分引用自北京大学机器学习公开课在前面的博文中已经学习了构建神经网络的基础需求，搭建了一个简单的双层网络结构来实现数据的分类。并且了解了激活函数和损失函数在神经网络中发挥的重要用途，其中，激活函数优化了神经元的输出能力，损失函数优化了反向传播时参数更新的趋势。我们知

优化器（一）torch.optim.SGD-随机梯度下降法

torch.optim.SGD-随机梯度下降法 import torchimport torchvision.datasetsfrom torch import nnfrom torch.utils.data import DataLoaderdataset = torchvision.datasets.CIFAR10(root='./data', train=False, downloa

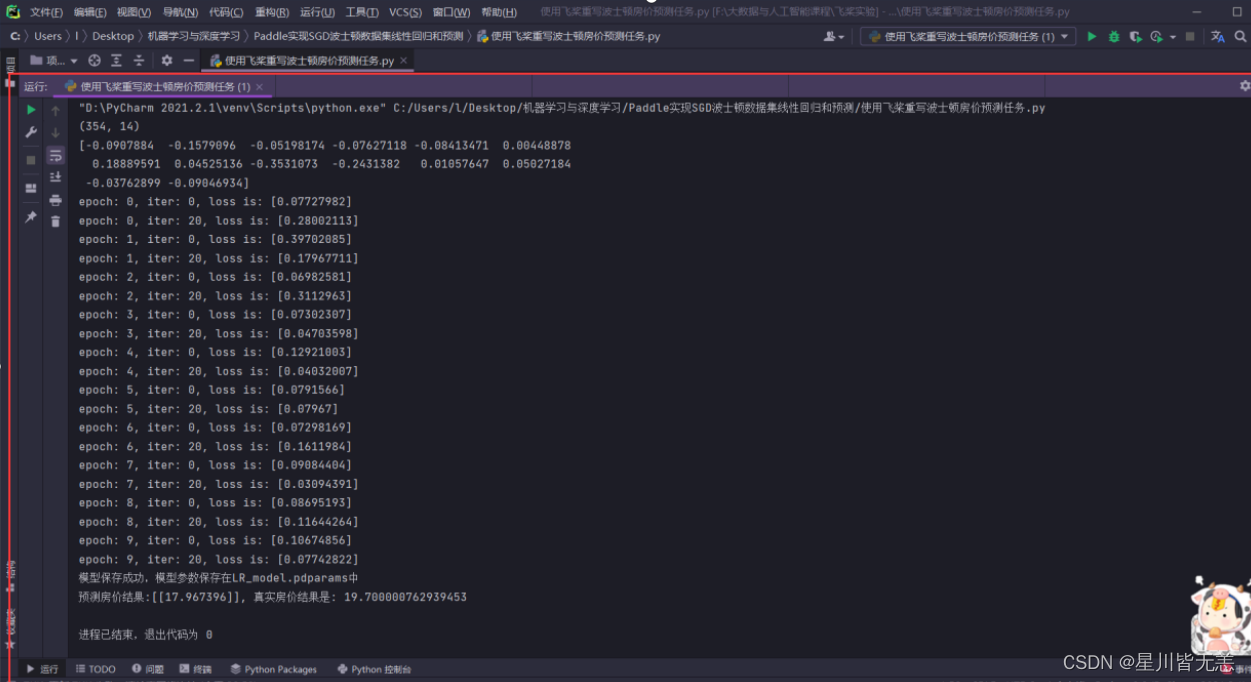
机器学习与深度学习——使用paddle实现随机梯度下降算法SGD对波士顿房价数据进行线性回归和预测

文章目录机器学习与深度学习——使用paddle实现随机梯度下降算法SGD对波士顿房价数据进行线性回归和预测一、任务二、流程三、完整代码四、代码解析五、效果截图机器学习与深度学习——使用paddle实现随机梯度下降算法SGD对波士顿房价数据进行线性回归和预测随机梯度下降（SGD）也称为增量梯度下降，是一种迭代方法，用于优化可微分目标函数。该方法通过在小批量数据上计算损失函数

梯度下降、随机梯度下降(SGD)、批量梯度下降(BGD)的对比

转载自：http://blog.csdn.net/lilyth_lilyth/article/details/8973972 梯度下降（GD）是最小化风险函数、损失函数的一种常用方法，随机梯度下降和批量梯度下降是两种不同的迭代求解思路，下面从公式和实现的角度对两者进行分析。下面的h(x)是要拟合的函数，J(theta)损失函数，theta是参数，要迭代求解的值，theta求解出来了那最终要拟

SGD-adam-adamw

title: SGD && Adam && Adamw的C语言实现以及对比总结 date: 2023-03-08 17:08:50 tags: SGD && Adam && Adamw的C语言实现以及对比总结文章目录 title: SGD && Adam && Adamw的C语言实现以及对比总结 date: 2023-03-08 17:08:50 tags: SGD && Adam

神经网络优化算法如何选择Adam，SGD

链接：https://blog.csdn.net/u014381600/article/details/72867109/ Adam更适合于稀疏矩阵的优化。之前在tensorflow上和caffe上都折腾过CNN用来做视频处理，在学习tensorflow例子的时候代码里面给的优化方案默认很多情况下都是直接用的AdamOptimizer优化算法，如下： optimizer = tf.trai

斯坦福机器学习 Lecture2 （假设函数、参数、样本等等术语，还有批量梯度下降法、随机梯度下降法 SGD 以及它们的相关推导，还有正态方程）

假设函数定义假设函数，猜一个 x->y 的类型，比如 y = ax + b，随后监督学习的任务就是找到误差最低的 a 和 b 参数有时候我们可以定义 x0 = 1，来让假设函数的整个表达式一致统一如上图是机器学习中的一些术语额外的符号，使用 (xi, yi) 表示第 i 个样本 n 表示特征数量（在房屋价格预测问题中，属性/特征有两个：房子面积和卧室数量，因此这里 n =