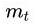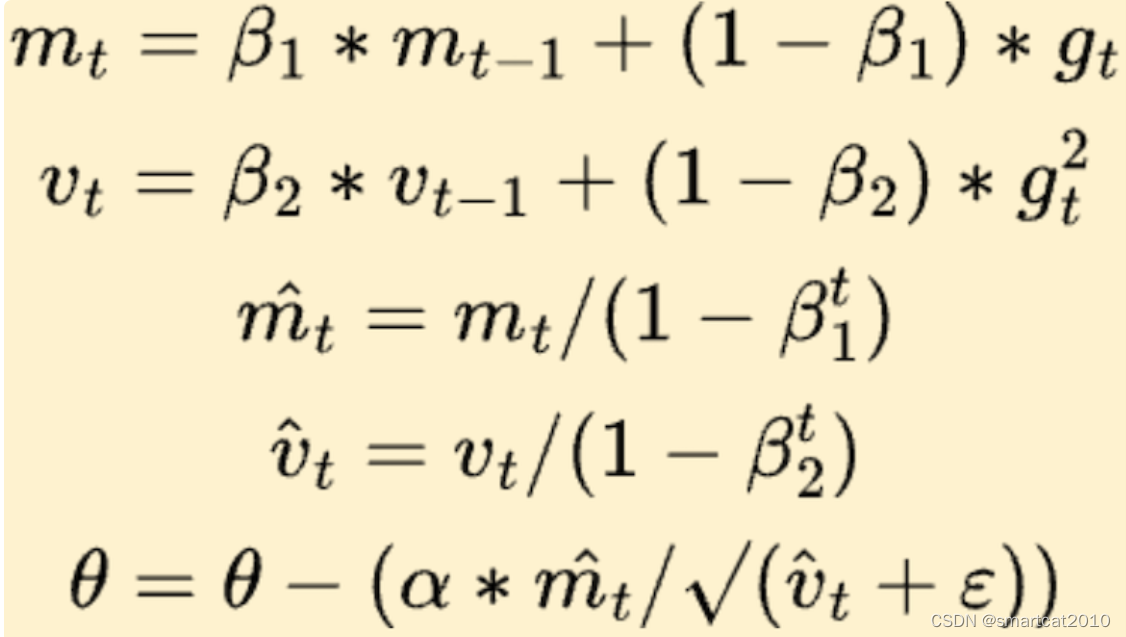SGD-adam-adamw

title: SGD && Adam && Adamw的C语言实现以及对比总结
date: 2023-03-08 17:08:50
tags:

SGD && Adam && Adamw的C语言实现以及对比总结

SGD(随机梯度下降法，stochastic gradient descent)

概述：大多数机器学习或者深度学习的算法都涉及某种形式的优化。优化指的是通过改变x的值来最大化或最小化f(x)的任务。我们通常以最小化f(x)来指代大多数的优化问题。最大化可经由最小化算法-f(x)实现。

我们把要最小化或最大化的函数称为目标函数或准则。 当我们对其进行最小化时，我们也把它称为代价函数、损失函数或误差函数。

下面我们假设一个损失函数：
$$J(\theta )=\frac{1}{2}(h(x)-y{)}^2$$
其中，
$$h_{\theta }(x)={\theta }_0+{\theta }_{1x_1}+{\theta }_{2x_2}+\dots +{\theta }_{n{x}_n}$$
然后要使得最小化它。

$$梯度下降：我们知道曲面上方向导数的最大值的方向就代表了梯度的方向，因此我们在做梯度下降的时候，应该是沿着梯度的反方向进行权重的更新，可以有效的找到全局的最优解。这个{\theta }_i的更新过程可以描述为：$$

$${\theta }_j={\theta }_j-\alpha \frac{({\partial \frac{1}{2}{h}_{\theta }(x)-y)}^2}{\partial {\theta }_i}$$

$$=(h{}_{\theta }x-y)x_j$$

(中间推导过程省略，只给出结果)
$$其中\alpha 指的是学习率（步长），我把它设为0.01$$
下面给出题目，用SGD求解在x = 5附近 f(x) 的极值。
$$f(x)=sin(x{)}^2+cos(x)+5$$
给出C语言实现的代码

#include<math.h>
#include<stdio.h>
#include<stdlib.h>
//原函数y = sin(x)^2 + cos(x) + 5
double function(double x){double y = pow(sin(x),2) + cos(x) + 5;return y;
}//偏导数
double d_x(double x){double d_y = 2*sin(x)*cos(x) - sin(x);return d_y;
}int main(){int step = 0;double rate = 1e-2, y_new, new_theta=6, theta = 6, eps = 0.000002,lamita = 0.00001;while(fabs(d_x(new_theta)) > eps) {new_theta = theta - rate * d_x(theta);theta = new_theta;y_new = function(theta);printf("step: %d: x=%.5lf, y=%.5lf\n", step++, theta, y_new);}	return 0;
}

这里注意：当学习率过大时，可能导致在不能最优值之间收敛，忽略了最优值的位置。

而学习率过小时，收敛速度过慢，有可能陷入局部最优解，而忽略了全局最优解。

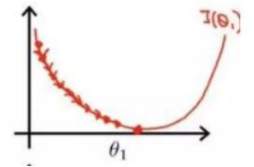
Adam

adam伪代码

Adam与经典的随机梯度下降法是不同的。随机梯度下降保持一个单一的学习速率(称为alpha)，用于所有的权重更新，并且在训练过程中学习速率不会改变。每一个网络权重(参数)都保持一个学习速率，并随着学习的展开而单独地进行调整。该方法从梯度的第一次和第二次矩的预算来计算不同参数的自适应学习速率。

在梯度变化比较大时，学习率变化较快。在梯度变化比较小时，学习率变化比较慢。

这里给出题目：
$$f(x)=sin(x{)}^2+cos(x)+5$$
下面给出C语言实现公式：

#include<stdio.h>
#include<stdlib.h>
#include<math.h>//原函数y = sin(x)^2 + cos(x) + 5
double function(double x){double y = pow(sin(x),2) + cos(x) + 5;return y;
}//偏导数
double d_x(double x){double d_y = 2*sin(x)*cos(x) - sin(x);return d_y;
}int main(){int step = 0;double mt , m = 1 , m_1 , vt , v = 1 ,v_1, beita_1 = 0.9 , beita_2 = 0.999;double rate = 1e-3, y_new, new_theta=6, theta = 6, eps = 0.000002,lamita = 0.00001;while(fabs(d_x(new_theta)) > eps) {step ++;mt = beita_1 * m + (1-beita_1)*d_x(theta);m = mt;vt = beita_2 * v + (1-beita_2)*pow(d_x(theta),2);v = vt;m_1 = mt / (1 + pow(beita_1,step));v_1 = vt / (1 - pow(beita_2,step));new_theta = theta - rate * mt/(sqrt(vt)+1e-8 );theta = new_theta;y_new = function(theta);printf("step: %d: x=%.5lf, y=%.5lf\n", step, theta, y_new);}	return 0;
}

Adamw

下面来看Adamw 的伪代码

以及具体的C语言实现：

#include<stdio.h>
#include<math.h>
#define PI 3.14159265358979//原函数y = sin(x)^2 + cos(x) + 5
double function(double x){double y = pow(sin(x),2) + cos(x) + 5;return y;
}//偏导数
double d_x(double x){double d_y = 2*sin(x)*cos(x) - sin(x);return d_y;
}int main(){int step = 0;double mt , m = 1 , m_1 , vt , v = 1 ,v_1, beita_1 = 0.9 , beita_2 = 0.999;double rate = 1e-2, y_new, new_theta=6, theta = 6, eps = 0.000002,lamita = 0.00001;while(fabs(d_x(new_theta)) > eps) {step ++;mt = beita_1 * m + (1-beita_1)*d_x(theta);m = mt;vt = beita_2 * v + (1-beita_2)*pow(d_x(theta),2);v = vt;m_1 = mt / (1 + pow(beita_1,step));v_1 = vt / (1 - pow(beita_2,step));new_theta = theta - rate * (mt/(sqrt(vt)+rate + 0.0001 * theta));theta = new_theta;y_new = function(theta);printf("step: %d: x=%.5lf, y=%.5lf\n", step, theta, y_new);}	return 0;
}

SGD && Adam && Adamw之间比较

首先在速度方面，很显然：SGD < adam < adamw

SGD最大的缺点是下降速度慢，而且可能会在沟壑的两边持续震荡，停留在一个局部最优点。

下面是上述测试SGD运行的情况：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VZkWiK7x-1678443875709)(/home/thy/.config/Typora/typora-user-images/image-20230310174329559.png)]

adam测试结果：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BPOI9iRS-1678443875709)(/home/thy/.config/Typora/typora-user-images/image-20230310174623272.png)]

adamw测试结果：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EYLvf92W-1678443875710)(/home/thy/.config/Typora/typora-user-images/image-20230310174902193.png)]

SGD缺点：容易困在局部最优的沟壑里面。

Adam缺点：
Adam缺点一：可能不收敛

SGD没有用到二阶动量，因此学习率是恒定的。而Adam的二阶动量随着固定时间窗口内的积累，使得vt可能会时大时小，不是单调变化。这就可能在训练后期引起学习率的震荡，导致模型无法收敛。

Adam缺点二：可能错过全局最优解

在训练时包含大量的参数，在这样一个维度极高的空间内，非凸的目标函数往往起起伏伏，拥有无数个高地和洼地。有的是高峰，通过引入动量可能很容易越过；但有些是高原，可能探索很多次都出不来，于是停止了训练。