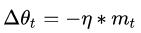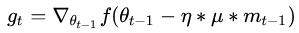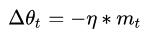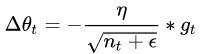本文主要是介绍SGD,Momentum,AdaGrad,RMSProp,Adam等优化算法发展历程,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
各种优化算法层出不穷,看的眼花缭乱,如果不能理清楚其中他们的关系及发展历程,必然会记得很混乱及模糊
最开始做神经网络的时候大家更新参数的时候都是把所有数据计算一遍,求所以数据的平均梯度再进行参数调节,后来觉得这样太慢了,干脆就计算一条数据就调节一次,这就叫随机梯度下降了(SGD),随机两字的由来是因为每条数据可能调节的方向都不一样,下降的过程会很震荡。
这都是两个极端,后来就干脆折中一点,MIni batch进行一次调整,就是算出来了一个批次后调整一次,就是批梯度下降了。
然后可以想象一个石头落下山的时候肯定中间会收到阻力,忽而慢、忽而快,在我们这里就好比如,如果前面的批次都是朝着一个方向进行调整,突然有个异常数据方向完全相反或又差异,岂不是一种干扰,辛辛苦苦调整了半天又回去了,这个时候一个大神就想到了物理里面的动量,模拟石头下山的一个过程,一路顺畅则越下越快,有阻碍则减速,这就是动量下降法(Momentum)
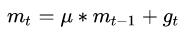
但是如果都是一路顺畅,会下降的过快,在达到终点的时候可能会溢出,所以又改进了一点产生了牛顿动量法(Nesterov),其核心思想是:注意到 momentum 方法,如果只看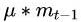
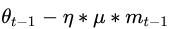
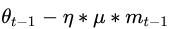
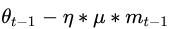
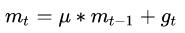
在约束完梯度后,就开始对学习率进行改进了
AdaGrad 对于出现频率较低参数采用较大的α更新;相反,对于出现频率较高的参数采用较小的α更新。
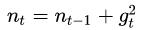
随着训练次数的增加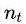
RMSprop算法 AdaGrad 是学习率除以梯度的平方和开根号,RMs则变为了求梯度平方和的平均数开根号(均方根)
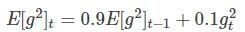
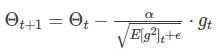
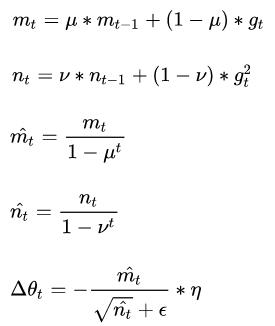
其中,,分别是对梯度的一阶矩估计和二阶矩估计,可以看作对期望,的估计;,是对,的校正,这样可以近似为对期望的无偏估计,为什么要进行这么一个无偏估计呢,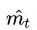
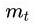
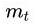
这篇关于SGD,Momentum,AdaGrad,RMSProp,Adam等优化算法发展历程的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!