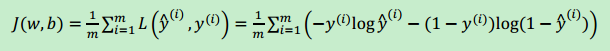logistic专题

【ML--04】第四课 logistic回归

1、什么是逻辑回归？当要预测的y值不是连续的实数（连续变量），而是定性变量（离散变量），例如某个客户是否购买某件商品，这时线性回归模型不能直接作用，我们就需要用到logistic模型。逻辑回归是一种分类的算法，它用给定的输入变量（X）来预测二元的结果（Y）（1/0,是/不是，真/假）。我们一般用虚拟变量来表示二元/类别结果。你可以把逻辑回归看成一种特殊的线性回归，只是因为最后的结果是类别变

NumPy实现logistic回归

1.sklearn实现 import numpy as npimport matplotlib.pyplot as pltimport pandas as pdimport osimport sysfrom sklearn.model_selection import train_test_splitfrom sklearn.preprocessing import Standard

初学logistic回归

一、简介假设现在有一些数据点，我们用一条直线对这些点进行拟合，这个拟合的过程就称作回归。Logistic回归的主要思想是：根据现有数据对分类边界线建立回归方式，以此进行分类。这是一个二值型输出分类器。由于需要进行距离计算，以此要求数据类型为数值型。二、基本思想我们想要的函数是能够接受所有的输入然后预测出类别。我们此处用的函数是Sigmoid函数，Sigmoid函数具体的计算方式

Logistic Regression本质上还是Linear Regression的一种，只是用了一个Logistic Function将线性回归的连续值映射到了 { 0 , 1 } \{0, 1\} {0,1}空间。因此Linear Regression只能对具有线性边界的分类问题有很好的预测效果，对于非线性的边界是无能为力的。至于下面这张很经典的大家常用的图，只是做了一个feature map

ython机器学习分类算法（六）-- 逻辑回归（Logistic Regression）

逻辑回归原理逻辑回归虽然名为“回归”，但实际上是一种用于处理二分类或多分类问题的分类算法。其核心思想是，利用线性回归模型的预测结果逼近真实标记的对数几率（log odds），因此得名“逻辑回归”。具体来说，逻辑回归通过引入sigmoid函数（或称为逻辑函数），将线性回归模型的输出值映射到0和1之间，从而可以将其解释为某个类别发生的概率。对于二分类问题，假设输

如何通俗理解逻辑回归(Logistic Regression)

首先, 什么是逻辑回归呢? 我们先来看一下逻辑回归的公式: t = w T X + b y = s i g m o i d ( t ) s i g m o i d ( t ) = 1 1 + e − t t = w^TX+b\\ y = sigmoid(t)\\ sigmoid(t) = \frac1{1+e^{-t}} t=wTX+by=sigmoid(t)sigmoid(t)=1+e−t1

第100+11步 ChatGPT学习：R实现Logistic分类

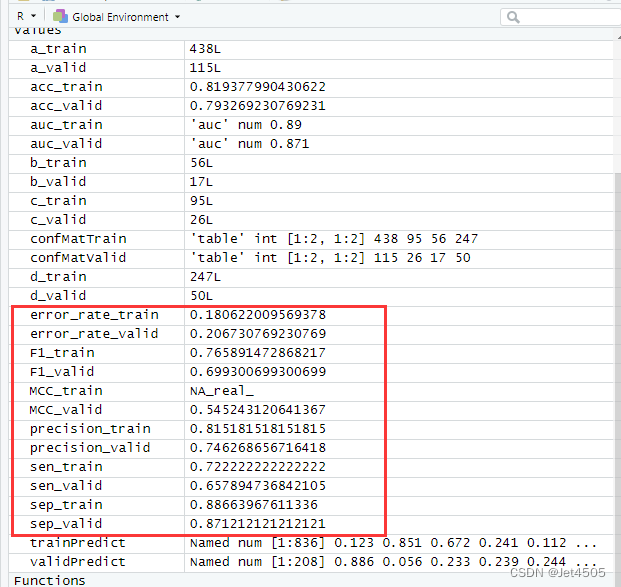
基于R 4.2.2版本演示一、写在前面有不少大佬问做机器学习分类能不能用R语言，不想学Python咯。答曰：可！用GPT或者Kimi转一下就得了呗。加上最近也没啥内容写了，就帮各位搬运一下吧。二、R代码实现Logistic分类（1）导入数据我习惯用RStudio自带的导入功能：（2）建立LR模型 # Load necessary libraries

Logistic函数与Logistic回归

Logistic函数与Logistic回归 Logistic函数的表示形式如下：它的函数图像如下，由于函数图像很像一个“S”型，所以该函数又叫 sigmoid 函数。满足的性质： 1.对称性，关于(0,0.5)中心对称 2.逻辑斯谛方程即微分方程最早logistic函数是皮埃尔·弗朗索瓦·韦吕勒在1844或1845年在研究它与人口增长的关

联合数据库，申请出战！新指标“超级老人”揭示老年健康新视角，仅用logistic分析发文二区...

说到老年数据库，大家最熟悉的肯定是Charls，实际上类似免费好用的老年数据库还有很多，在没有思路的时候我们不妨看一下其他数据库的文章，说不定能找到新的思路或者切入点。今天介绍的这篇文章就提出来一个新的概念-“超级老人”，并联合了多个数据库发文二区！让我们一起往下看吧！ 2024年6月1日，外国学者做了一项研究，在期刊《Journals of Gerontology Series B-psy

史上最直白的logistic regression教程之二

实现线性拟合我们用python2.7实现上一篇的推导结果。请先安装python matplotlib包和numpy包。具体代码如下: #!/usr/bin/env python #! -*- coding:utf-8 -*-import matplotlib.pyplot as pltfrom numpy import *#创建数据集def load_dataset():n = 1

【python】python化妆品销售logistic逻辑回归预测分析可视化（源码+课程论文+数据集）【独一无二】

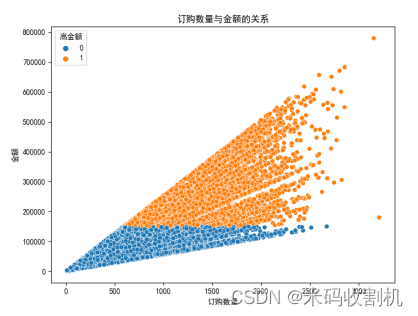
👉博__主👈：米码收割机 👉技__能👈：C++/Python语言 👉公众号👈：测试开发自动化【获取源码+商业合作】 👉荣__誉👈：阿里云博客专家博主、51CTO技术博主 👉专__注👈：专注主流机器人、人工智能等相关领域的开发、测试技术。系列文章目录目录系列文章目录一、功能设计项目代码设计重点提取二、数据可视化三、逻辑回归模型构建与评估

PyTorch学习5：Logistic回归

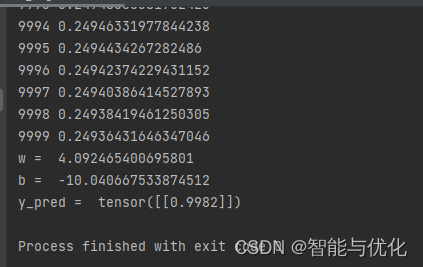
文章目录前言一、分类问题简介二、示例1.示例步骤2.示例代码总结前言介绍利用PyTorch实现Logistic回归的分类问题一、分类问题简介分类问题的输出为属于每一个类别的概率，概率值最大的即为所属类别。最常见的Sigmoid函数：Logistic函数。二、示例 1.示例步骤 1.构建模型 class LogisticRegressionModel(t

Logistic回归（对数几率回归）笔记

回归：假设有一些数据点，用一条直线对这些点进行拟合的过程(成为最佳拟合直线)，叫做回归。 Logistic回归进行分类的思想是：根据现有数据对分类边界建立回归公式，以此进行分类。训练分类器时的做法就是寻找最佳拟合参数，使用的是最优化算法。 i i i表示第?个训练样本， y ^ \widehat{y} y 表示预测值。损失函数（误差函数）： L ( y ^ , y ) = −

Logistic逻辑回归模型(LR)基础

逻辑回归(Logistic Regression, LR)模型其实仅在线性回归的基础上，套用了一个逻辑函数，但也就由于这个逻辑函数，使得逻辑回归模型成为了机器学习领域一颗耀眼的明星，更是计算广告学的核心。本文主要详述逻辑回归模型的基础，至于逻辑回归模型的优化、逻辑回归与计算广告学等，请关注后续文章。 1 逻辑回归模型回归是一种极易理解的模型，就相当于y=f(x)，表明自变量x与

算法金 | 你真的完全理解 Logistic 回归算法了吗

大侠幸会，在下全网同名「算法金」 0 基础转 AI 上岸，多个算法赛 Top 「日更万日，让更多人享受智能乐趣」今日 178/10000 1. 引言吴恩达：机器学习的六个核心算法！，通透！！十大回归算法模型最强总结，突破最强算法模型，决策树算法！！急匆匆把逻辑回归给落下了，今天我们杀他个回马枪，再战三百回合逻辑回归 Logistic 回归是一种用于分类问题

【逻辑回归】Logistic Regression逻辑回归模型学习笔记

文章目录序言1. 线性回归2. 逻辑回归2.1 引入逻辑回归的原因2.2 逻辑回归2.3 逻辑回归的应用 3. 逻辑函数3.1 sigmoid函数3.2 sigmoid函数的性质3.3 决策边界3.4 对数几率 4. 损失函数4.1 为什么说逻辑回归时概率类模型4.2 为什么要进行极大似然估计4.3 利用MLE如何推导出损失函数4.4 损失函数/代价函数/目标函数 5. 最优化问题6. s

使用logistic regression 处理良/恶性肿瘤分类任务案例

1.读入数据 2.随机切分数据集，把数据集切分成训练集和测试集 3.对数据集进行标准化 4.创建logistic regression 模型，在训练集上训练数据 5.在测试集上进行预测分类 logistic regression 预测的准确率：0.9883040935672515 # -*- coding:utf-8 -*-import pandas as pdimport num

机器学习模型以及优缺点——logistic

logistic回归核心：通过sigmoid函数或者softmax函数将线性模型拟合值映射到分类概率上，并通过最大似然或者最小化交叉熵函数来获得最优系数优点： 1.模型简单，训练速度较快，分类的时候，计算量仅仅只和特征的数目相关 2.较好的可解释性，参数的正负、绝对值大小代表了对应特征对于预测类别的重要性 3.极好的可并行性，优化目标相对参数的凸函数有全局最优解缺点： 1.不能用Logi

机器学习笔记5：Softmax分类器的logistic回归

在logistic回归模型中，我们只是讲了二分类问题，但是在我们的实际分类应用中，还涉及多分类问题，那么，这个时候，就需要用到softmax分类器了。如下图：有绿三角、红叉和蓝矩形三个类别要分类，我们是通过三个分类器先分别将绿三角、红叉、蓝矩形分类出来，这样处理多分类问题的，所以对每个类别c，训练一个logistic回归分类器 f w c ( x ) f_{\textbf{w}}^{c}(\t

机器学习笔记4：Logistic 回归模型

Logistic回归的基本原理logistic回归的优化算法前言：在分类任务中，我们是通过从输入 x x x到输出 y y y的映射 f f f的模型得出来的：　　　　　　　　　　　 y ^ = f ( x ) = a r g m a x p ( y = c ∣ x , D ) \hat{y}=f(x)=arg maxp(y=c|\mathbf{x},D) y^=f(x)=argmaxp

数字水印 | 混沌逻辑斯谛映射（Chaotic Logistic Map）基本原理及 Python 代码实现

目录 1 基本原理2 代码实现3 分岔图代码实现 1 基本原理参考：维基百科 - 逻辑斯谛映射逻辑斯谛映射（Logistic Map）是一种二次多项式的映射递推关系式，是一个由简单非线性方程式产生混沌现象的经典范例。其数学表达为： x n + 1 = μ x n ( 1 − x n ) x_{n+1}=\mu x_n(1-x_n) xn+1=μxn(1−x

【机器学习】三、逻辑回归(Logistic Regression)

目录背景逻辑回归算法目标算法推演逻辑函数（Logstic Function) 假设函数代价函数（Cost Function) 梯度下降函数算法实现案例案例分析及代码实现读取数据特征选择参数theta定义代价函数梯度下降最小化拟合主函数结果验证图形化展示背景本文内容所使用的python包及别名：（pytho

【机器学习读书笔记】Logistic回归

【机器学习读书笔记】Logistic回归四、Logistic回归 Logistic回归属于广义线性回归模型，通过历史数据的表现对未来结果发生的概率进行预测，它属于分类和预测算法中的一种。他是用来解决二值分类（binary classification）,AndrewNG忠告：不要用线性回归去解决分类问题。逻辑回归的回归方程和线性回归相比，在其基础上增加了一个逻辑函数（logistic函数

Python大数据分析——Logistic回归模型

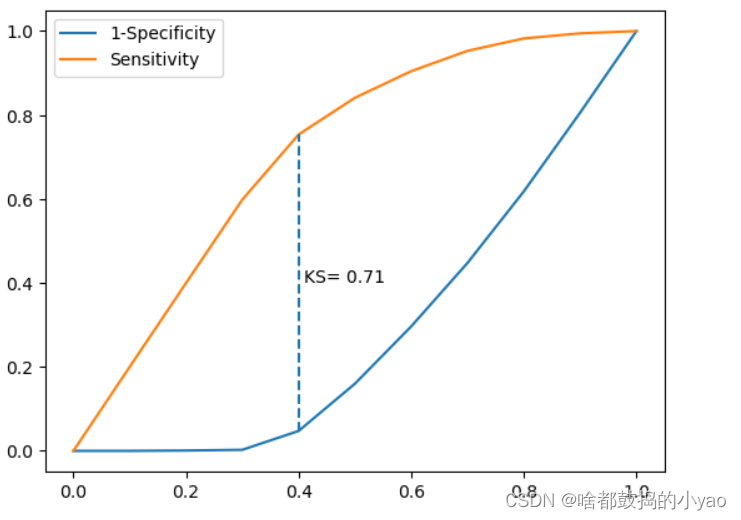
Logistic回归模型概念理论分析模型评估混淆矩阵ROC曲线KS曲线函数示例概念之前的回归的变量是连续的数值变量；而Logistics回归是二元离散值，用来解决二分类问题。理论分析上式中的hβ(X)也被称为Loqistic回归模型，它是将线性回归模型的预测值经过非线性的Logit函数转换为[0,1]之间的概率值。其函数图像为：其中，z∈(-∞,+∞)。

deeplearning.ai 吴恩达网上课程学习（四）——Logistic代码实战，基于Linux，Python 3.4

此文章偏向于实践和自己的理解，本文讲述了Python代码的一些基本操作，由浅入深最后实现logistic的代码。(原文中代码实现基于jupyter notebook，文中代码实现基于之前搭建的Linux的Python平台，二者代码会有细小的区别。搭建平台的链接深度学习（一）：搭建TensorFlow) 原创内容来自： https://www.missshi.cn/api/view/blog

MLA Review之四：logistic回归

终于来到logistic回归，logistic回归其实很简单，之前的说到的神经网络就用到了这个方法，其中最重要的就是使用了sigmoid损失函数。当然使用的方法也就最简单的梯度下降法，这里并没有使用之前神经网络的随机梯度下降法，也是为了简单起见。因为之前在神经网络里面使用过了，所以这篇文章就略微介绍下。 logistic回归是属于广义线性回归的一种，基本形式： z=w0+w1*x