机器学习笔记5：Softmax分类器的logistic回归

本文主要是介绍机器学习笔记5：Softmax分类器的logistic回归，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在logistic回归模型中，我们只是讲了二分类问题，但是在我们的实际分类应用中，还涉及多分类问题，那么，这个时候，就需要用到softmax分类器了。如下图：

有绿三角、红叉和蓝矩形三个类别要分类，我们是通过三个分类器先分别将绿三角、红叉、蓝矩形分类出来，这样处理多分类问题的，所以对每个类别c，训练一个logistic回归分类器$f_{\text{w}}^c(\text{x})$，预测概率为y=c；当输入一个新的$\text{x}$时，选择使的$f_{\text{w}}^c(\text{x})$最大的类别作为其预测。
那么，对于我们的分类器，将从sigmoid(对应二项分布)扩展为softmax函数(对应多项分布Cat):
　　　　　　　
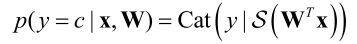
softmax函数类似取最大函数：$S(\eta {)}_c=\frac{exp({\eta }_c)}{{\sum }_{c^{\prime }=1}^{C}exp({\eta }_{c^{\prime }})}$
综合起来：
　　　　　　　　
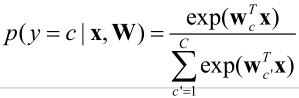
softmax回归
引入记号：
　　　　　　　　
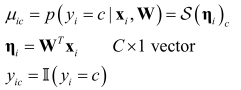
则负似然函数：
　　　　　　
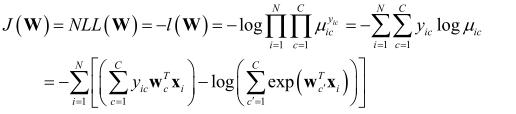
梯度：
　　　　　　
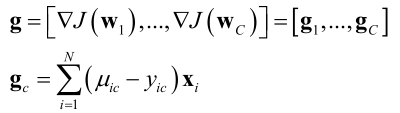
Hessian矩阵为正定：
　　　　　　
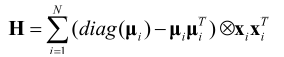
softmax分类器能够实现多分类功能，是对logistic回归在两分类上的扩展，其优化算法与两类分的logistic回归类似，这里就不累述了。

这篇关于机器学习笔记5：Softmax分类器的logistic回归的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---