分类器专题
理解分类器(linear)为什么可以做语义方向的指导?(解纠缠)
Attribute Manipulation(属性编辑)、disentanglement(解纠缠)常用的两种做法:线性探针和PCA_disentanglement和alignment-CSDN博客 在解纠缠的过程中,有一种非常简单的方法来引导G向某个方向进行生成,然后我们通过向不同的方向进行行走,那么就会得到这个属性上的图像。那么你利用多个方向进行生成,便得到了各种方向的图像,每个方向对应了很多
Spark2.x 入门:决策树分类器
一、方法简介 决策树(decision tree)是一种基本的分类与回归方法,这里主要介绍用于分类的决策树。决策树模式呈树形结构,其中每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。学习时利用训练数据,根据损失函数最小化的原则建立决策树模型;预测时,对新的数据,利用决策树模型进行分类。 决策树学习通常包括3个步骤:特征选择、决策树的生成和决策树的剪枝。
用opencv的traincascade.exe训练行人的HAAR、LBP和HOG特征的xml文件,并对分类器进行加载和检测
看到一篇论文上讲到可以用adaboost分类器进行行人检测,就想自己动手训练一下分类器,折腾了两周终于训练成功了。。。 opencv中有两个函数可以训练分类器opencv_haartraining.exe和opencv_traincascade.exe,前者只能训练haar特征,后者可以用HAAR、LBP和HOG特征训练分类器。这两个函数都可以在opencv\build\x86\vc10\bin
NLP-信息抽取:关系抽取【即:三元组抽取,主要用于抽取实体间的关系】【基于命名实体识别、分词、词性标注、依存句法分析、语义角色标注】【自定义模板/规则、监督学习(分类器)、半监督学习、无监督学习】
信息抽取主要包括三个子任务: 实体抽取与链指:也就是命名实体识别关系抽取:通常我们说的三元组(triple)抽取,主要用于抽取实体间的关系事件抽取:相当于一种多元关系的抽取 一、关系抽取概述 关系抽取通常在实体抽取与实体链指之后。在识别出句子中的关键实体后,还需要抽取两个实体或多个实体之间的语义关系。语义关系通常用于连接两个实体,并与实体一起表达文本的主要含义。常见的关系抽取结果
KNN分类器-Java实现
KNN,即K近邻算法。其基本思想或者说是实现步骤如下: (1)计算样本数据点到每个已知类别的数据集中点的距离 (2)将(1)中得到的距离按递增顺序排列 (3)选取(2)中前K个点(即与当前样本距离最小的K个已知类别的数据点) (4)统计(3)中得到的K个点所在类别的出现频率 (5)返回(4)中出现频率最高的类别作为样本点的预测类别 在给出具体实现代码之前,说明一点:Java下的矩阵操作
libtorch---day02[第一个分类器]
参考pytorch。 加载数据集CIFAR10 因为例程中使用的是torchvision加载数据集CIFAR10,但是torchvision的c++版本提供的功能太少,不考虑使用了,直接下载bin文件进行读取加载,CIFAR10数据格式: CIFAR-10 数据集的图像数据以二进制格式存储。数据集中每张图像由以下几个部分组成: 标签 (1 byte): 表示图像所属的类别(0-9)。
Darknet训练分类器
Table of Contents 一:安装darknet 二:数据处理,准备train.list test.list labels.txt 三:制作数据集配置文件 四:制作网络 五:开始训练 六:测试及验证 七:中断后重新训练 一:安装darknet git clone https://github.com/AlexeyAB/darknet/cd darknetma
智能优化特征选择|基于鲸鱼WOA优化算法实现的特征选择研究Matlab程序(XGBoost分类器)
智能优化特征选择|基于鲸鱼WOA优化算法实现的特征选择研究Matlab程序(XGBoost分类器) 文章目录 一、基本原理鲸鱼智能优化特征选择流程 二、实验结果三、核心代码四、代码获取五、总结 智能优化特征选择|基于鲸鱼WOA优化算法实现的特征选择研究Matlab程序(XGBoost分类器) 一、基本原理 当然,这里是鲸鱼智能优化算法(WOA)与XGBoost分类器结
机器学习——贝叶斯分类器
一、贝叶斯决策论 贝叶斯决策论是概率框架下实施决策的基本方法。 假设有 N N N种可能的类别标记,即 Y = { c 1 , c 2 , . . . , c N } Y=\{c_1,c_2,...,c_N \} Y={c1,c2,...,cN}, λ i j \lambda_{ij} λij是将一个真实标记为 c j c_j cj的样本误分类为 c i c_i ci所产生的
sklearn光速入门实践[1]——实现一个简单的SVM分类器
python的sklearn库封装了许多常用的机器学习算法,而且入门简单,调用方便。下面我们用sklearn库和简单的几个点作为数据集,来实现一个简单的SVM分类器。 首先,准备好数据。我们把(2,0),(0,2),(0,0)这三个点当作类别1;(3,0),(0,3),(3,3)这三个点当作类别2,训练好SVM分类器之后,我们预测(-1,-1),(4,4)这两个点所属的类别。示意图如下: 1
六. 部署分类器-int8-calibration
目录 前言0. 简述1. 案例运行2. 补充说明3. 代码分析3.1 main.cpp3.2 trt_model.cpp3.3 trt_calibrator.hpp3.4 trt_calibrator.cpp 4. 校准精度影响因素结语下载链接参考 前言 自动驾驶之心推出的 《CUDA与TensorRT部署实战课程》,链接。记录下个人学习笔记,仅供自己参考 本次课程我们来学习
从零开始学习深度学习库-6:集成新的自动微分模块和MNIST数字分类器
在上一篇文章中,我们完成了自动微分模块的代码。深度学习库依赖于自动微分模块来处理模型训练期间的反向传播过程。然而,我们的库目前还是“手工”计算权重导数。现在我们拥有了自己的自动微分模块,接下来让我们的库使用它来执行反向传播吧! 此外,我们还将构建一个数字分类器来测试一切是否正常工作。 使用自动微分模块并非必要,不使用这个模块也没事,用原本的方法也能很好地工作。 然而,当我们开始在库中实现更复
SVM(Support Vector Machine)分类器详解
1. 拉格朗日乘子(Lagrange multiplier)法求解条件极值 1.1 拉格朗日乘子的简单描述 简单的条件极值问题可以描述为:求函数 z = f ( x , y ) z=f(x,y) z=f(x,y)的最大值,且 x , y x,y x,y满足约束条件 φ ( x , y ) = M \varphi (x,y)=M φ(x,y)=M( M M M已知)。 拉格朗日乘子的求解步骤为:
Naive Bayes分类器详解
##1. 贝叶斯定理 假设随机事件 A A A发生的概率是 P ( A ) P(A) P(A),随机事件 B B B发生的概率为 P ( B ) P(B) P(B),则在已知事件 A A A发生的条件下,事件 B B B发生的概率为: P ( B ∣ A ) = P ( A ∣ B ) P ( B ) P ( A ) P(B|A) = \frac {P(A|B)P(B)}{P(A)} P(B∣A
AI学习指南机器学习篇-朴素贝叶斯分类器
AI学习指南机器学习篇-朴素贝叶斯分类器 1. 介绍 在机器学习中,朴素贝叶斯分类器是一种简单而有效的分类算法。它基于贝叶斯定理和特征条件独立性假设,可以被用来解决多种分类问题。本篇博客将深入探讨朴素贝叶斯分类器的基本原理,包括如何进行分类预测,以及“朴素”的含义和特征条件独立性的假设。 2. 基本原理 2.1 贝叶斯定理 贝叶斯定理是描述随机事件发生概率的公式,它表达了在已知某一事件发
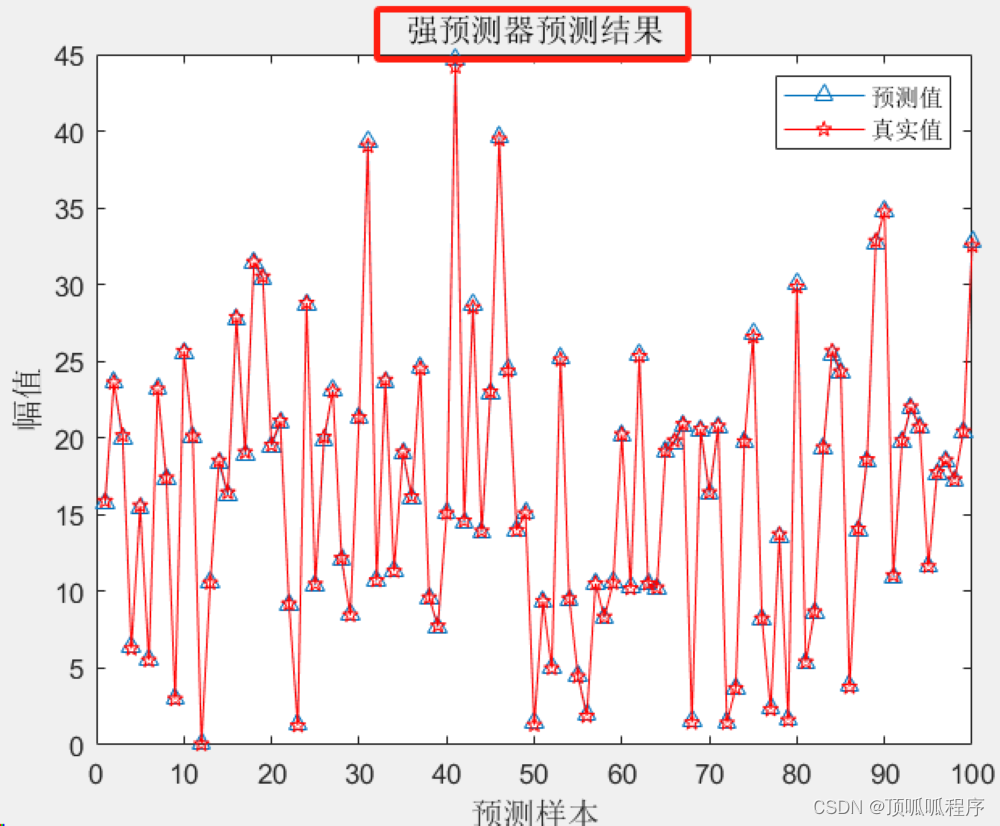
2-11 基于matlab的BP-Adaboost的强分类器分类预测
基于matlab的BP-Adaboost的强分类器分类预测,Adaboost是一种迭代分类算法,其在同一训练集采用不同方法训练不同分类器(弱分类器),并根据弱分类器的误差分配不同权重,然后将这些弱分类器组合成一个更强的最终分类器(强分类器),并一直迭代,直到分类的错误率达到之前设定的阈值或者迭代次数达到设定最大迭代次数。程序已调通,可直接运行。 2-11 BP-Adaboost 分类器分类预
三种特征分类器Haar、LBP和HOG
最常用到的三种特征分别为Haar特征、LBP特征及HOG特征,三种特征描述了三种不同的局部信息: Haar描述的是图像在局部范围内像素值明暗变换信息; LBP描述的是图像在局部范围内对应的纹理信息; HOG描述的则是图像在局部范围内对应的形状边缘梯度信息。 三种特征在图像处理和机器学习领域都得到了广泛的应用,在此做一个总结,方便后面复习。 版本历程 1) Haar:因为之前
官方文档-opencv训练级联分类器
indexnext |previous |OpenCV 2.3.2 documentation »OpenCV用户指南 » 级联分类器训练 介绍 级联分类器包括两部分:训练和检测。检测部分在OpenCV objdetect 模块的文档中有介绍,在那文档中给出了一些级联分类器的基本介绍。这个指南是描述如何训练分类器:准备训练数据和运行训练程序。 重点注意事项 OpenCV中有两
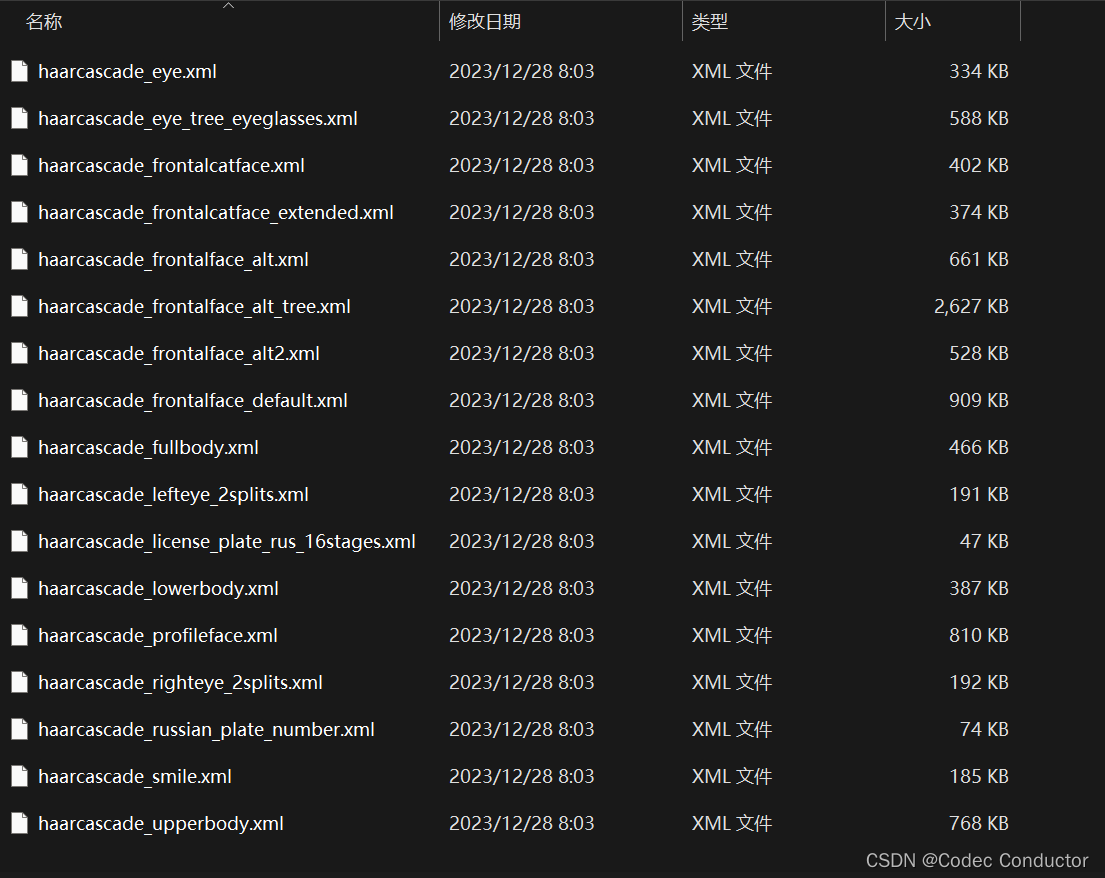
OpenCV中 haarcascades 级联分类器各种模型.xml文件介绍
haarcascades Haar Cascades 是一种用于对象检测的机器学习模型,特别是在OpenCV库中广泛使用。这些模型通过训练大量的正样本(包含目标对象的图像)和负样本(不包含目标对象的图像)来识别图像中的对象。Haar Cascades 模型通常以XML文件的形式提供,可以直接加载到OpenCV程序中使用。 OpenCV中已经包含了许多预先训练好的Haar Cascades分类器
朴素贝叶斯分类器 #数据挖掘 #Python
朴素贝叶斯分类器是一种基于概率统计的简单但强大的机器学习算法。它假设特征之间是相互独立的(“朴素”),尽管在现实世界中这通常不成立,但在许多情况下这种简化假设仍能提供良好的性能。 基本原理:朴素贝叶斯分类器利用贝叶斯定理,计算给定输入特征条件下属于某个类别的概率,并选择具有最高概率的那个类别作为预测结果。计算公式:对于特征向量 ( x ) 和类别 ( C ),朴素贝叶斯估计为 ( P(C|X)
【深度学习】Transformer分类器,CICIDS2017,入侵检测,随机森林、RFE、全连接神经网络
文章目录 1 前言2 随机森林训练3 递归特征消除 RFE Recursive feature elimination4 DNN5 Transformer5.1. 输入嵌入层(Input Embedding Layer)5.2. 位置编码层(Positional Encoding Layer)5.3. Transformer编码器层(Transformer Encoder Layer)5.4
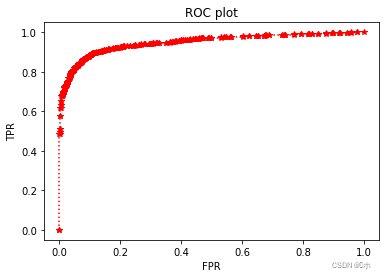
模式识别分类器评价指标之ROC曲线
ROC(Receiver Operating Characteristic Curve)接收器操作特性曲线,原先主要用于评价雷达中的漏报虚警等事件的指标,其中漏报表示雷达监控的空域中有敌机出现,而雷达没能检测出来;虚警则表示雷达监控的空域中没有敌机出现,而雷达却发出警报。后来ROC曲线又用在了医学分类指标中,主要是二分类,即有病/没病,后逐渐扩展到模式识别的多分类中,用来评价分类器的好坏。在ROC
分类器模型评价指标之ROC曲线
来源:分类器模型评价指标 An introduction to ROC analysis Spark mllib 自带了许多机器学习算法,它能够用来进行模型的训练和预测。当使用这些算法来构建模型的时候,我们需要一些指标来评估这些模型的性能,这取决于应用和和其要求的性能。Spark mllib 也提供一套指标用来评估这些机器学习模型。 具体的机器学习算法归入更广泛类型的机器学习应用,例如:分
模式识别分类器评价指标之CMC曲线
CMC曲线全称是Cumulative Match Characteristic (CMC) curve,也就是累积匹配曲线,同ROC曲线Receiver Operating Characteristic (ROC) curve一样,是模式识别系统,如人脸,指纹,虹膜等的重要评价指标,尤其是在生物特征识别系统中,一般同ROC曲线一起给出,能够综合评价出算法的好坏。如下图所示: 那么,CMC曲
深度学习 --- stanford cs231 编程作业(assignment1,Q2: SVM分类器)
stanford cs231 编程作业之SVM分类器 写在最前面: 深度学习,或者是广义上的任何学习,都是“行千里路”胜过“读万卷书”的学识。这两天光是学了斯坦福cs231n的一些基础理论,越往后学越觉得没什么。但听的云里雾里的地方也越来越多。昨天无意中在这门课的官网上无意中看到了对应的assignments。里面的问题和code都设计的极好!自己在做作业的时候,也才
Matlab分类器大全
train_data是训练特征数据, train_label是分类标签。 Predict_label是预测的标签。 MatLab训练数据, 得到语义标签向量 Scores(概率输出)。 1.逻辑回归(多项式MultiNomial logistic Regression) Factor = mnrfit(train_data, train_label);Scores = mnrval(Fa




![libtorch---day02[第一个分类器]](https://i-blog.csdnimg.cn/direct/dfedb2b2bafd40eebd42ce0b9bd27193.png)


![sklearn光速入门实践[1]——实现一个简单的SVM分类器](https://i-blog.csdnimg.cn/blog_migrate/37b1cd9f70b70b7a88429c60af5e31b8.png)