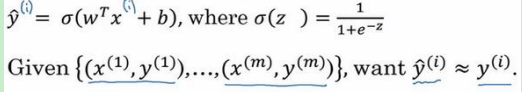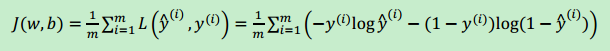本文主要是介绍Logistic回归(对数几率回归)笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
回归:假设有一些数据点,用一条直线对这些点进行拟合的过程(成为最佳拟合直线),叫做回归。
Logistic回归进行分类的思想是:根据现有数据对分类边界建立回归公式,以此进行分类。
训练分类器时的做法就是寻找最佳拟合参数,使用的是最优化算法。
i i i表示第?个训练样本, y ^ \widehat{y} y 表示预测值。
损失函数(误差函数):
L ( y ^ , y ) = − y l o g ( y ^ ) − ( 1 − y ) l o g ( 1 − y ^ ) L(\widehat{y}, y) = -ylog(\widehat{y}) - (1-y)log(1-\widehat{y}) L(y ,y)=−ylog(y )−(1−y)log(1−y )
损失函数是在单个训练样本中定义的,它衡量的是算法在单个训练样本中表现如何,
代价函数(成本函数):为了衡量算法在全部训练样本上的表现如何,算法的代价函数是对?个样本的损失函数求和然后除以?:
损失函数只适用于像这样的单个训练样本,而代价函数是参数的总代价,所以在训练逻
辑回归模型时候,我们需要找到合适的?和?,来让代价函数 ? 的总代价降到最低。
Logistic回归分类器实现:
在每个特征上都乘以一个回归系数,将所有的结果相加,总和代入Sigmoid函数中,得到范围在0~1之间的数值。任何大于0.5的数据分为1类,小于0.5分为0类。所以,Logistic回归也可以被看成一种概率估计。
y = 1 1 + e − z y=\frac{1}{1 + e^{-z}} y=1+e−z1
y = 1 1 + e − ( W T X + b ) y=\frac{1}{1 + e^{-(W^TX+b)}} y=1+e−(WTX+b)1
向量W就是最佳参数
基于最优化方法的最佳回归系数确定
Sigmoid函数的输入记为z:
z = w 0 x 0 + w 1 x 1 + w 2 x 2 + . . . + w n x n = W T X z=w_{0}x_{0}+w_{1}x_{1}+w_{2}x_{2}+...+w_{n}x_{n}=W^{T}X z=w0x0+w1x1+w2x2+...+wnxn=WTX
向量x是分类器的输入数据,向量w是需要找到的最佳参数。
梯度下降法
假定代价函数 ?(?) 只有一个参数?,即用一维曲线代替多维曲线,这样可以更好画出图像
w : = w − a d J ( w ) d w w :=w - a\frac{dJ(w)}{dw} w:=w−adwdJ(w)
b : = b − a d J ( b ) d b b := b - a\frac{dJ(b)}{db} b:=b−adbdJ(b)
? 表示学习率(learning rate),用来控制步长(step),即向下走一步的长度,
d J ( w ) d w \frac{dJ(w)}{dw} dwdJ(w)就是函数?(?)对? 求导(derivative)。
梯度算子总是指向函数值减小最快的方向,a为步长,该公式将一直被迭代执行,直至达到某个停止条件为止,比如迭代次数达到某个值或算法达到可以允许的范围误差。
随机梯度下降法
梯度下降法在每次更新回归系数时都要遍历整个数据集,计算量大。一种改进方法是一次仅用一个样本点来更新回归系数,称为随机梯度下降法。由于可以在新样本到来时对分类器进行增量式更新,所以是一个在线学习算法,一次处理所有数据被称为“批处理”。
伪代码:
每个回归系数初始化为1
对数据中的每个样本
计算该样本的梯度
使用alpha * gradient更新回归系数的向量
返回回归系数
mini-batch 梯度下降法
batchsize = ? => batch梯度下降法
batchsize = 1 => 随机梯度下降法
m为训练集样本数量
参考:
DeepLearning.ai 深度学习课程笔记(V5.47) 黄海广
Machine Learning in Action 机器学习实战 【美】Peter Harrington
这篇关于Logistic回归(对数几率回归)笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!