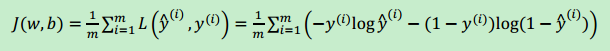对数专题
Flink实时计算指标对数方案
来源:大数据技术与架构读者投稿 作者:诸葛子房 点击右侧关注,大数据开发领域最强公众号! 点击右侧关注,暴走大数据! By 大数据技术与架构 作者简介: 诸葛子房 ,目前就职于一线互联网公司,从事大数据相关工作,了解互联网、大数据相关内容,一直在学习的路上 。
数据结构基础之《(2)—对数器》
一、认识对数器 1、你在网上找到了某个公司的面试题,你想了好久,感觉自己会做,但是你找不到在线测试, 2、你和朋友交流面试题,你想了好久,感觉自己会做,但是你找不到在线测试 3、你在网上做笔试,但是前几个测试用例都过了,突然一个巨大无比数据量来了,结果你的代码报错了,如此大的数据量根本看不出哪错了 二、对数器怎么用 1、你想要测的方法a(你设计的流程时间复杂度低,但是不知道对不对) 2、实现
【HDU】5958 New Signal Decomposition【离散对数下的FFT】
题目链接:【HDU】5958 New Signal Decomposition 在此先感谢小q对我的指导,没有q老师的帮助,估计永远也做不出来了。 首先我们考虑对这个式子做离散对数。令 g g为pp的某个原根,则有: bi=∑p−1j=0aj⋅r(i,j) \quad b_i=\sum_{j=0}^{p-1}a_j\cdot r(i,j) bi=∑p−1j=0aj⋅2sin32πi⋅j
Xilinx实现对数运算
简介 本章节实现任意底数和真数值的转换,设计中一般有两种实现方法: 1、在外部直接算好对数值,按照数值范围做个表,存在ram里,到时候查表。为了减少表深度,提高资源利用率,可以考虑去掉部分低位数值,损失一定的精度。 2、log10(x)=ln(x) * log10(e) , log10(e)是常数可以手动先计算好,其中LN(X)使用IP实现计算
用Python解决预测问题_对数线性模型模板
对数线性模型(Log-linear model)是统计学中用于分析计数数据或频率数据的一类模型,特别是在多维列联表(contingency tables)分析中非常常见。这种模型通过取对数将乘法关系转换为加法关系,从而简化了数据分析。 在对数线性模型中,我们通常对观测频数的对数进行建模,模型的形式可以表示为: 对数线性模型可以用于检验因子之间的独立性,以及估计不同因子水平组合下的预期频数。
pytorch负对数似然损失函数介绍
nn.NLLLoss(负对数似然损失)是 PyTorch 中的一种损失函数,常用于分类任务,特别是在模型的输出已经经过了 log-softmax 的情况下。与 nn.CrossEntropyLoss 不同的是,nn.NLLLoss 期望输入的是对数概率值(即 log-softmax 的输出),而不是未经过处理的 logits。 Log-Softmax函数是对Softmax函数的对数版本,它在
opencv实现对数log灰度变换
我的思路太窄了,想了一个遍历的方法。也可以先做通道分解,分析单个通道的log变换。 菜鸟一个,若是有好的想法,还请赐教。 Mat log_image;log_image.create(512,512,CV_8UC1);cvtColor(input_image, input_image, CV_BGR2GRAY);for (int i = 0; i <512; i++){for (
复分析——第3章——亚纯函数和对数(E.M. Stein R. Shakarchi)
第3章 亚纯函数和对数 (Meromorphic Functions and the Logarithm) One knows that the differential calculus, which has contributed so much to the progress of analysis, is founded on the consideration of diffe
编写程序,键盘输入x和y的值,计算并输出表达式 ln(3x-1)/y的值。要求设置异常处理,对除0、负数求对数两种情况进行异常捕捉处理(math.log)
a=ln(3x-1)/ydef except_test(x,y):try: #检查是否为0或复数if y<=0:print("不好意思,请输入大于0的数字")result=math.log(3*x-1)/yreturn resultexcept ValueError as e:print(f"报错信息为:{e}")except Exception as e:print(f"异常信息为:{e
力扣2300.咒语和药水的成功对数
力扣2300.咒语和药水的成功对数 排序 + 二分 对于能整除的数 -1以后一起处理可以在原数组直接修改 class Solution {public:vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {sort(potions.begin(),potions
hdu 4911 归并 求逆序对对数(Java实现)
网页链接 Inversion Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others) Total Submission(s): 1962 Accepted Submission(s): 765 Problem Description bobo ha
Logistic回归(对数几率回归)笔记
回归:假设有一些数据点,用一条直线对这些点进行拟合的过程(成为最佳拟合直线),叫做回归。 Logistic回归进行分类的思想是:根据现有数据对分类边界建立回归公式,以此进行分类。 训练分类器时的做法就是寻找最佳拟合参数,使用的是最优化算法。 i i i表示第?个训练样本, y ^ \widehat{y} y 表示预测值。 损失函数(误差函数): L ( y ^ , y ) = −
算法学习笔记——对数器
对数器 对数器的实现: 你想要测的方法a(最优解)实现复杂度不好但是容易实现的方法b(暴力解)实现一个随机样本产生器(长度也随机、值也随机)把方法a和方法b跑相同的输入样本,看看得到的结果是否一样如果有一个随机样本使得比对结果不一致,打印这个出错的样本进行人工干预,改对方法a和方法b当样本数量很多时比对测试依然正确,可以确定方法a(最优解)已经正确。 关键是第5步,找到一个数据量小的错误样本
二分查找,查找第一个大于目标元素target所对应的下标-2300. 咒语和药水的成功对数
题目链接及描述 2300. 咒语和药水的成功对数 - 力扣(LeetCode) 题目分析 这道题目作为一个典型的二分查找,题目中所述,找到每一个spells[i]在positions中对应的元素positions[i]使其乘积大于给定元素sucess,并统计每一个spell[i]所对应的positions中所查找元素的个数,并将其返回。 本题本质思想并不
LeetCode2300咒语和药水的成功对数
题目描述 解析 先对药水排序后每个咒语去二分查找最低满足的药水的位置。 class Solution {public int[] successfulPairs(int[] spells, int[] potions, long success) {int n = spells.length, m = potions.length;Arrays.sort(potions);for
Android Audio System线性音量和对数音量的转换
Android的音频系统的代码中,应用程序对每个音频流的音量做出调整后,最终会转换为一个系数K,所有的音频数据在输出到硬件之前,都要乘以系数K,只要应用程序发出调整音量的调用,中间层的Audio System就会重新计算系数K的值。对应用程序来说,音量控制通常都是按照线性进行调整的,比如对于具有15级音量的音频流来说,我们预期每级的音量变化都是相当的,也就是说:从第5级调到第6级,和从第7级调到第
Code13 数组中左边大于2倍右边数的总对数
数组 [6,4,2,1] 其中(6,2)(6,1)(4,1)这3个组合是满足左边大于右边数的两倍 核心代码块,建立在归并排序的基础上 int ans = 0;int windowR = M+1;for (int j = L;j<=M;j++){while (windowR <= R && arr[j] > (arr[windowR]*2)){windowR ++;}ans += window
Java Math函数中的指数与对数之旅
1. 概述 Java中的Math类包含了一组用于执行指数与对数运算的方法。这些方法允许我们计算数值的指数、自然对数、常用对数以及幂运算。这些函数在数学计算、物理模拟、工程分析以及金融计算等领域都有广泛的应用。 2. 用途 指数和对数函数在数学和科学计算中起着基础而重要的作用。指数函数用于描述增长和衰减过程,而对数函数则用于解决与比例、对数尺度相关的问题。幂运算则是更一般化的指数运算,用于
matlab 对数坐标画图,及在曲线上加竖直线
matlab 对数坐标画图 方法一:直接对x、y值取对数,然后画图 plot(log(x), log(y), 'm', 'LineWidth',1, 'Marker','.');% ,'Color','#EDB120' 方法二:将x、y轴刻度改为对数形式 plot(x, y, 'r', 'LineWidth',1, 'Marker','+');ax = gca();% 获取当前坐标句柄
西瓜书学习——对数几率回归
对数几率回归(Logistic Regression)是一种广泛应用于分类问题的统计方法,特别是用于二分类问题。尽管它的名字中包含“回归”,但它实际上是一种分类算法,用于估计一个样本属于某个类别的概率。 对数几率回归的核心是使用逻辑函数(Logistic Function),也称为 sigmoid 函数,将线性回归的输出映射到 0 和 1 之间的概率。sigmoid 函数定义为: S ( x
灰度变换,gama变换,对数,反对数变换
学习DIP第2天 灰度变换,及按照一定规则对像素点的灰度值进行变换,变换的结果可以增强对比度,或者达到其他的效果(例如二值化,或者伽马变换),由于灰度变换为针对单个像素点的灰度值进行变换,素以算法复杂度一般为O(W*H)(图像宽和高) 完整内容迁移至 https://face2ai.com/DIP-1-2-灰度变换-gama变换-对数-反对数变换/ http://www.to
LR为什么取log损失函数,又为什么在似然函数计算之后取对数
在学习和做项目的过程中,逐渐加深了对LR的理解。 其中最重要的一点就是为什么取-log函数为损失函数,损失函数的本质就是,如果我们预测对了,能够不惩罚,如果预测错误,会导致损失函数变得很大,也就是惩罚较大,而-log函数在【0,1】之间正好符合这一点,另外还有一点需要说明,LR是一种广义的线性回归模型,平方损失函数的话,对于Sigmoid函数求导计算,无法保证是凸函数,在优化的过程中,求得的解有
对拍器/对数器 赛前抱佛脚
“对拍器/对数器的使用前提是该题你会暴力解法,如果不会,那么对拍器/对数器也没啥用。” 对拍器/对数器 应用背景 你有一个绝对对的暴力cpp代码,但时间会T,只适用于小范围的数据。所以你写了一个聪明的非暴力cpp代码,但是不知道对不对。 如果非暴力代码是对的,那么在同一份数据上,非暴力代码和暴力代码的结果应该是一样的。根据这个我们就需要一个随机生成数据的mkd.cpp代码了。 工作流
蓝桥杯练习:友好的对数
时间限制:1.0s 内存限制:256.0MB 问题描述 有两个整数,如果每个整数的约数和(除了它本身以外)等于对方,我们就称这对数是友好的。例如: 9的约数和有:1+3=4 4的约数和有:1+2=3 所以9和4不是友好的。 220的约数和有:1 2 4 5 10 11 20 22 44 55 110=284 284的约数和有:1 2 4 71 142=220 所以220