本文主要是介绍机器学习笔记4:Logistic 回归模型,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
- Logistic回归的基本原理
- logistic回归的优化算法
前言:
在分类任务中,我们是通过从输入 x x x到输出 y y y的映射 f f f的模型得出来的:
y ^ = f ( x ) = a r g m a x p ( y = c ∣ x , D ) \hat{y}=f(x)=arg maxp(y=c|\mathbf{x},D) y^=f(x)=argmaxp(y=c∣x,D)
其中,我们定义 y y y为离散值,其取值范围称之为标签空间: y = { 1 , 2 , . . , C } y=\left \{ 1,2,..,C \right \} y={1,2,..,C}; 当 C = 2 C=2 C=2为二分类问题,这时候的分布为bernoulli分布,该分布的概率表示:
p ( y ∣ x ) = B e r ( y ∣ μ ( x ) ) p(y|\mathbf{x})=Ber(y|\mu (\textbf{x})) p(y∣x)=Ber(y∣μ(x))
其中 μ ( x ) = E ( y ∣ x ) = p ( y = 1 ∣ x ) \mu(\mathbf{x})=E(y|\mathbf{x})=p(y=1|\mathbf{x}) μ(x)=E(y∣x)=p(y=1∣x)
我们复习下Bernoulli分布的概念:
Bernoulli分布又称两点分布或0-1分布。若是Bernoulli试验成功,则Bernoulli随机变量 X X X取值为1,否则为0。记试验成功的概率为 θ \theta θ,我们称 X X X服从参数为 θ \theta θ的Bernoulli分布,记为 X B e r ( θ ) X~Ber(\theta) X Ber(θ),概率函数(pmf)为:
p ( x ) = θ x ( 1 − θ ) ( 1 − x ) = { θ i f x = 1 1 − θ i f x = 0 } p(x)=\theta^{x}(1-\theta)^{(1-x)}=\begin{Bmatrix} \theta & if x=1 \\ 1-\theta& ifx=0 \end{Bmatrix} p(x)=θx(1−θ)(1−x)={θ1−θifx=1ifx=0}
其中 Bernoulli分布的均值: μ = θ \mu=\theta μ=θ,方差: σ 2 = θ ∗ ( 1 − θ ) \sigma ^{2}=\theta \ast (1-\theta) σ2=θ∗(1−θ)
1、logistic的基本原理
Logistic回归模型跟线性回归模型一样,也是线性模型,只是其条件概率 p ( y ∣ x ) p(y|\mathbf{x}) p(y∣x)的形式不同:
p ( y ∣ x ) = B e r ( y ∣ μ ( x ) ) p(y|\textbf{x})=Ber(y|\mu (\textbf{x})) p(y∣x)=Ber(y∣μ(x))
μ ( x ) = σ ( w T x ) \mu (\textbf{x})=\sigma (\textbf{w}^{T}\textbf{x}) μ(x)=σ(wTx)
其中sigmoid函数(S函数,图如下)定义为
σ ( a ) = 1 1 + e x p ( − a ) \sigma (a)=\frac{1}{1+exp(-a)} σ(a)=1+exp(−a)1
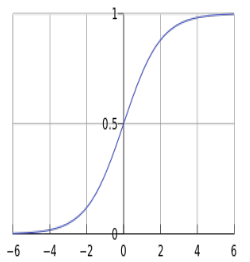
上述函数我们亦可以称为logistic函数或者logit函数,将实数 a a a变切换到[0,1]区间。而且有因为该函数取值在[0,1]区间,所以logistic回归又被称为logit回归。
为什么使用logistic函数呢,因为在神经科学中,神经元的对其输入进行加权和: f ( x ) = w T x f(x)=\textbf{w}^{T}\textbf{x} f(x)=wTx,如果该和大于某个阈值(即: f ( x ) > τ f(x)>\tau f(x)>τ)的话,则神经元发放脉冲。而且,在logistic回归中,我们定义Log Odds Radio:
L O R ( x ) = log p ( 1 ∣ x , w ) p ( 0 ∣ x , w ) = log [ 1 1 + e x p ( − w T x ) 1 + e x p ( − w T x ) e x p ( − w T x ) ] LOR(\textbf{x})=\log\frac{p(1|\textbf{x},\textbf{w})}{p(0|\textbf{x},\textbf{w})}=\log[\frac{1}{1+exp(-\textbf{w}^{T}\textbf{x})}\frac{1+exp(-\textbf{w}^{T}\textbf{x})}{exp(-\textbf{w}^{T}\textbf{x})}] LOR(x)=logp(0∣x,w)p(1∣x,w)=log[1+exp(−wTx)1exp(−wTx)1+exp(−wTx)]
= log ( e x p ( w T x ) = w T x =\log(exp(\textbf{w}^{T}\textbf{x})=\textbf{w}^{T}\textbf{x} =log(exp(wTx)=wTx
因此,如果 L O R ( x ) = w T x > 0 LOR(\textbf{x})=\textbf{w}^{T}\textbf{x}>0 LOR(x)=wTx>0,则神经元发放脉冲,即 p ( 1 ∣ x , w ) > p ( 0 ∣ x , w ) p(1|\textbf{x},\textbf{w})>p(0|\textbf{x},\textbf{w}) p(1∣x,w)>p(0∣x,w)
那么在logistic回归中,当:
L O R ( x ) = w T x > 0 LOR(\textbf{x})=\textbf{w}^{T}\textbf{x}>0 LOR(x)=wTx>0 时, y ^ = 1 \hat{y}=1 y^=1
L O R ( x ) = w T x < 0 LOR(\textbf{x})=\textbf{w}^{T}\textbf{x}<0 LOR(x)=wTx<0 时, y ^ = 0 \hat{y}=0 y^=0
w T x = 0 \textbf{w}^{T}\textbf{x}=0 wTx=0时为决策面。因此 a ( x ) = w T x a(\textbf{x})=\textbf{w}^{T}\textbf{x} a(x)=wTx为分类决策面,故logistic回归是一个线性分类器。
2、logistic回归的优化算法
我们知道logistic回归的概率函数为: p ( y ∣ x ) = B e r ( y ∣ μ ( x ) ) p(y|\textbf{x})=Ber(y|\mu (\textbf{x})) p(y∣x)=Ber(y∣μ(x)),则令 μ i = μ ( x i ) \mu_{i}=\mu(\textbf{x}_{i}) μi=μ(xi),则负log似然为:
J ( w ) = N L L ( w ) = − ∑ i = 1 N log [ ( μ i ) y i ∗ ( 1 − μ i ) ( 1 − y i ) ] J(\textbf{w})=NLL(\textbf{w})=-\sum_{i=1}^{N}\log[(\mu_{i})^{y_{i}}\ast(1-\mu_{i})^{(1-y_{i})} ] J(w)=NLL(w)=−∑i=1Nlog[(μi)yi∗(1−μi)(1−yi)]
= ∑ i = 1 N − [ y i log ( μ i ) + ( 1 − y i ) log ( 1 − μ i ) ] =\sum_{i=1}^{N}-[y_{i}\log(\mu_{i})+(1-y_{i})\log(1-\mu_{i})] =∑i=1N−[yilog(μi)+(1−yi)log(1−μi)]
极大似然估计 等价于 最小logistic损失。那么 J ( w ) J(\textbf{w}) J(w)的优化求解可以使用梯度下降法或者牛顿法。
(1)梯度下降法

求解
其中:
算法与线性回归 g ( w ) = ∑ i = 1 N ( f ( x i ) − y i ) x i g(\textbf{w})=\sum_{i=1}^{N}(f(\textbf{x}_{i})-y_{i})\textbf{x}_{i} g(w)=∑i=1N(f(xi)−yi)xi看起来一样,只是 f ( x ) f(x) f(x)不一样,事实上所有的线性回归模型的梯度都是如此。

(2)牛顿法
牛顿法,其原则是使用函数 f ( x ) f(x) f(x)的泰勒级数的前几项来寻找方程 f ( x ) = 0 f(x)=0 f(x)=0的根。
我们知道一阶泰勒展开式: f ( x ) = f ( x t ) + f ′ ( x t ) ( x − x t ) f(x)=f(x^{t})+{f}'(x^{t})(x-x^{t}) f(x)=f(xt)+f′(xt)(x−xt)
所以,我们将导数 g ( w ) g(\textbf{w}) g(w)在 w t \textbf{w}^{t} wt处进行泰勒展开:
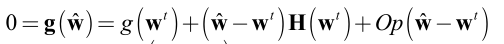
去掉高阶无穷小 O p ( w ^ − w t ) Op(\hat{\textbf{w}}-\textbf{w}^{t}) Op(w^−wt),得到:
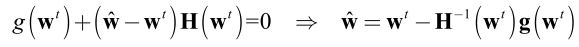
因此得到的迭代机制:
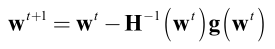
所以牛顿法又可以称为二阶梯度下降法,移动方向为: d = − ( H ( w t ) ) − 1 g ( w t ) d=-(H(\textbf{w}^{t}))^{-1}g(\textbf{w}^{t}) d=−(H(wt))−1g(wt);对比我们一阶梯度下降法,移动方向: d = − g ( w t ) d=-g(\textbf{w}^{t}) d=−g(wt)
损失函数的求解过程,我们还需要了解迭代在加权最小二乘(iterative reweighted least squares,IRLS)原则,何谓IRLS,上述我们以得出:
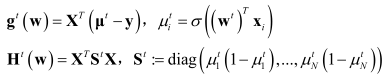
根据牛顿法的结果: 
所以IRLS:权重矩阵 S \textbf{S} S不是常数,而且依赖参数向量 w \textbf{w} w,我们必须使用标准方程来迭代计算,每次使用新的权重向量 w \textbf{w} w来修正权重矩阵 S \textbf{S} S。因此该算法称之为迭代再加权最小二乘,IRLS。
如下便是具体的公式迭代过程:

当然,上述是logistic回归没有正则化的过程,正则化logistic就是在 J ( w ) J(\textbf{w}) J(w)加上 λ ∣ ∣ w ∣ ∣ 2 \lambda ||\textbf{w}||^{2} λ∣∣w∣∣2(l2正则)或者 λ ∣ w ∣ \lambda |\textbf{w}| λ∣w∣(l1正则),同理求解过程结合线性回归模型的求解和上述不带正则的logistic回归的求解即可。
这篇关于机器学习笔记4:Logistic 回归模型的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







