ICP in PCL Registration

ICP in PCL Registration
点云配准是什么，维基百科上这样介绍：

Point cloud registration, is the process of finding a spatial transformation that aligns two point clouds. The purpose is to merge point clouds of multiple views into a globally consistent model.

在我的理解，有两个点集，source和target，target不变，source经过旋转（Rotation）和平移（Translation）甚至加上尺度（Scale）变换，使得变换后的source点集尽量和target点集重合，这个变换的过程就叫点集配准。 In the algorithm, target point cloud, is kept fixed, while the other one, the source, is transformed

to best match the reference. The algorithm iteratively revises the transformation (combination of

translation and rotation) needed to minimize the distance from the source to the reference point cloud.

    而ICP是最广泛应用的配准方法，也就是KinectFusion论文中所提到的ICP（ Iterative Closest Point ）， 最近邻迭代算法。icp利用迭代一步步地算出正确对应关系。

先上例子, 下面是用PCL中的icp配准两个点云：
void PairwiseICP(const pcl::PointCloud::Ptr &cloud_target, const pcl::PointCloud::Ptr &cloud_source, pcl::PointCloud::Ptr &output )
{
PointCloud::Ptr src(new PointCloud);
PointCloud::Ptr tgt(new PointCloud);

tgt = cloud_target;
src = cloud_source;pcl::IterativeClosestPoint<PointT, PointT> icp;
icp.setMaxCorrespondenceDistance(0.1);
icp.setTransformationEpsilon(1e-10);
icp.setEuclideanFitnessEpsilon(0.01);
icp.setMaximumIterations (100);icp.setInputSource (src);
icp.setInputTarget (tgt);
icp.align (*output);

// std::cout << “has converged:” << icp.hasConverged() << " score: " <<icp.getFitnessScore() << std::endl;

output->resize(tgt->size()+output->size());
for (int i=0;i<tgt->size();i++)
{output->push_back(tgt->points[i]);
}
cout<<"After registration using ICP:"<<output->size()<<endl;

}

   源码pcl.h里给出了Usage example， 源码从github上下载之后可以在这个目录找到 .\pcl-master\registration\include\pcl\registration。 这里可以看到两个重要信息：

一是PCL的icp里的transformation estimation是基于SVD的， SVD是奇异值分解，Singular Value Decomposition，后面我们会提到；
二是使用之前要至少set三个参数：
setMaximumIterations， 最大迭代次数，icp是一个迭代的方法，最多迭代这些次；
setTransformationEpsilon， 前一个变换矩阵和当前变换矩阵的差异小于阈值时，就认为已经收敛了，是一条收敛条件；
setEuclideanFitnessEpsilon， 还有一条收敛条件是均方误差和小于阈值， 停止迭代。
/** \brief @b IterativeClosestPoint provides a base implementation of the Iterative Closest Point algorithm.
* The transformation is estimated based on Singular Value Decomposition (SVD).
*
* The algorithm has several termination criteria:
*
*

• Number of iterations has reached the maximum user imposed number of iterations (via \ref setMaximumIterations)
• 
  *
• The epsilon (difference) between the previous transformation and the current estimated transformation is smaller than an user imposed value (via \ref setTransformationEpsilon)
• 
  *
• The sum of Euclidean squared errors is smaller than a user defined threshold (via \ref setEuclideanFitnessEpsilon)
• 
  *
  * Usage example:
  * …
  * \author Radu B. Rusu, Michael Dixon
  **/

      运行上面的代码就能得到两个点云配准的结果了，先不管结果好不好，看看他内部做了什么，实际配准算法都在aign里实现。icp.h里看到IterativeClosestPoint类是Registration的子类，icp.h给出了icp类的定义，而align的具体实现在上面的registration文件夹下的impl下的icp.hpp里，都说align with initial guess，如果可以从一个好的初始猜想变换矩阵开始迭代，那么算法将会在比较少的迭代之后就收敛，配准结果也较好，当像我们这里没有指定初始guess时，就默认使用单位阵Matrix4::Identity() ，迭代部分就像下面这样：
  

  // Repeat until convergence
  do
  {
  // Get blob data if needed
  PCLPointCloud2::Ptr input_transformed_blob;
  if (need_source_blob_)
  {
  input_transformed_blob.reset (new PCLPointCloud2);
  toPCLPointCloud2 (*input_transformed, *input_transformed_blob);
  }
  // Save the previously estimated transformation
  previous_transformation_ = transformation_;

  // Set the source each iteration, to ensure the dirty flag is updated
  correspondence_estimation_->setInputSource (input_transformed);
  if (correspondence_estimation_->requiresSourceNormals ())correspondence_estimation_->setSourceNormals (input_transformed_blob);
  // Estimate correspondences
  if (use_reciprocal_correspondence_)correspondence_estimation_->determineReciprocalCorrespondences (*correspondences_, corr_dist_threshold_);
  elsecorrespondence_estimation_->determineCorrespondences (*correspondences_, corr_dist_threshold_);//...size_t cnt = correspondences_->size ();
  // Check whether we have enough correspondences
  if (cnt < min_number_correspondences_)
  {PCL_ERROR ("[pcl::%s::computeTransformation] Not enough correspondences found. Relax your threshold parameters.\n", getClassName ().c_str ());convergence_criteria_->setConvergenceState(pcl::registration::DefaultConvergenceCriteria<Scalar>::CONVERGENCE_CRITERIA_NO_CORRESPONDENCES);converged_ = false;break;
  }// Estimate the transform
  transformation_estimation_->estimateRigidTransformation (*input_transformed, *target_, *correspondences_, transformation_);// Tranform the data
  transformCloud (*input_transformed, *input_transformed, transformation_);// Obtain the final transformation    
  final_transformation_ = transformation_ * final_transformation_;++nr_iterations_;converged_ = static_cast<bool> ((*convergence_criteria_));
  

  }
  while (!converged_);

  这里的 transformation_estimation_->estimateRigidTransformation (*input_transformed, *target_, *correspondences_, transformation_);做了最重要的估计变换矩阵， 实际是用pcl::registration::TransformationEstimationSVD类来实现的，这里至少有两个信息量，
  第一，SVD奇异值分解在pcl里是直接调用Eigen内部的Umeyama实现的，我看了一眼，太过数学，暂时跳过，在另一篇博客中提过，Eigen是专门处理矩阵运算的库，pcl用的3rdParty之一，pcl用了很多第三方，这也是为什么当初配环境如此痛苦的原因之一，毕竟pcl这个库最开始只是一个德国博士的毕业论文顺手写出来的； 另外还可以看到，这里的实现除了用SVD还有另一种方法，else里提到的是先算两个点云的3D Centeroid, 再getTransformationFromCorrelation. 后面我们再来提这种思路。
  第二， final_transformation = current_transformation * final_transformation, 这和KinFu那篇论文提到的“变换矩阵不断叠加，最终得到唯一的全局摄像头位置（global camera pose）”是一致的。

  template <typename PointSource, typename PointTarget, typename Scalar> inline void
  pcl::registration::TransformationEstimationSVD<PointSource, PointTarget, Scalar>::estimateRigidTransformation (
  ConstCloudIterator& source_it,
  ConstCloudIterator& target_it,
  Matrix4 &transformation_matrix) const
  {
  // Convert to Eigen format
  const int npts = static_cast (source_it.size ());

  if (use_umeyama_)
  {
  Eigen::Matrix<Scalar, 3, Eigen::Dynamic> cloud_src (3, npts);
  Eigen::Matrix<Scalar, 3, Eigen::Dynamic> cloud_tgt (3, npts);

  for (int i = 0; i < npts; ++i)
  {cloud_src (0, i) = source_it->x;cloud_src (1, i) = source_it->y;cloud_src (2, i) = source_it->z;++source_it;cloud_tgt (0, i) = target_it->x;cloud_tgt (1, i) = target_it->y;cloud_tgt (2, i) = target_it->z;++target_it;
  }// Call Umeyama directly from Eigen (PCL patched version until Eigen is released)
  transformation_matrix = pcl::umeyama (cloud_src, cloud_tgt, false);
  

  }
  else
  {
  source_it.reset (); target_it.reset ();
  // <cloud_src,cloud_src> is the source dataset
  transformation_matrix.setIdentity ();

  Eigen::Matrix<Scalar, 4, 1> centroid_src, centroid_tgt;
  // Estimate the centroids of source, target
  compute3DCentroid (source_it, centroid_src);
  compute3DCentroid (target_it, centroid_tgt);
  source_it.reset (); target_it.reset ();// Subtract the centroids from source, target
  Eigen::Matrix<Scalar, Eigen::Dynamic, Eigen::Dynamic> cloud_src_demean, cloud_tgt_demean;
  demeanPointCloud (source_it, centroid_src, cloud_src_demean);
  demeanPointCloud (target_it, centroid_tgt, cloud_tgt_demean);getTransformationFromCorrelation (cloud_src_demean, centroid_src, cloud_tgt_demean, centroid_tgt, transformation_matrix);
  

  }
  }

      到这里，pcl的算法基本上也捋清楚了，我们大概总结一下：首先icp是一步一步迭代得到较好的结果，解的过程其实是一个优化问题，并不能达到绝对正解。这个过程中求两个点云之间变换矩阵是最重要的，PCL里是用奇异值分解SVD实现的。 
  

  二. 各种ICP变种
  ICP有很多变种，有point-to-point的，也有point-to-plain的，一般后者的计算速度快一些，是基于法向量的，需要输入数据有较好的法向量，而法向量估计目前我对于自己的输入数据还没有很好的解决，具体使用时建议根据自己的需要及可用的输入数据选择具体方法。

  PCL里有很多ICP可以用 pcl::GeneralizedIterativeClosestPoint< PointSource, PointTarget >
  is an ICP variant that implements the generalized iterative closest point algorithm as described by Alex Segal et al.
  pcl::IterativeClosestPoint< PointSource, PointTarget, Scalar >
  provides a base implementation of the Iterative Closest Point algorithm.
  pcl::IterativeClosestPointWithNormals< PointSource, PointTarget, Scalar >
  is a special case of IterativeClosestPoint , that uses a transformation estimated based on Point to Plane distances by default.
  pcl::IterativeClosestPointNonLinear< PointSource, PointTarget, Scalar >
  is an ICP variant that uses Levenberg-Marquardt optimization backend.
  pcl::JointIterativeClosestPoint< PointSource, PointTarget, Scalar >
  extends ICP to multiple frames which share the same transform. pcl::registration::IncrementalICP< PointT, Scalar >
  This class provides a way to register a stream of clouds where each cloud will be aligned to the previous cloud.
  三. 广义配准Registration
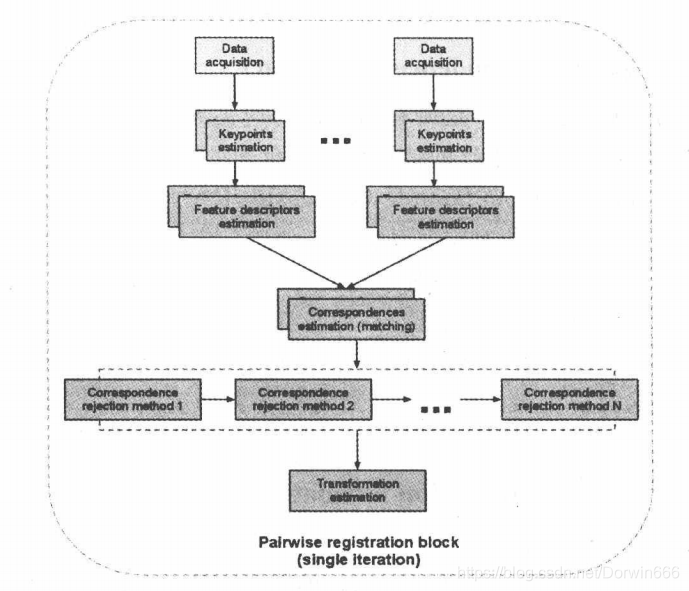
  Pairwise registration
  两个点集的对应，输出通常是一个4×4刚性变换矩阵：代表旋转和平移，它应用于源数据集，结果是完全与目标数据集匹配。下图是“双对应”算法中一次迭代的步骤：

  对两个数据源a，b匹配运算步骤如下：

  从其中一个数据源a出发，分析其最能代表两个数据源场景共同点的关键点k
  在每个关键点ki处，算出一个特征描述子fi
  从这组特征描述子{fi}和他们在a和b中的XYZ坐标位置，基于fi和xyz的相似度，找出一组对应
  由于实际数据源是有噪的，所以不是所有的对应都有效，这就需要一步一步排除对匹配起负作用的对应
  从剩下的较好对应中，估计出一个变换
  匹配过程中模块
  Keypoints（关键点）
  关键点是场景中有特殊性质的部分，一本书的边角，书上印的字母P都可以称作关键点。PCL中提供的关键点算法如NARF，SIFT，FAST。你可以选用所有点或者它的子集作为关键点，但需要考虑的是按毎帧有300k点来算，就有300k^2种对应组合。

  Feature descriptors（特征描述子）
  根据选取的关键点生成特征描述。把有用信息集合在向量里，进行比较。方法有：NARF, FPFH, BRIEF 或SIFT.

  Correspondences estimation（对应关系估计）
  已知从两个不同的扫描图中抽取的特征向量，找出相关特征，进而找出数据中重叠的部分。根据特征的类型，可以选用不同的方法。

  点匹配（point matching， 用xyz坐标作为特征），无论数据有无重组，都有如下方法：

  brute force matching（强制匹配）,
  kd-tree nearest neighbor search (FLANN)（kd树最近邻搜索）,
  searching in the image space of organized data（在图像空间搜索有组织的数据）,
  searching in the index space of organized data（按索引搜索有组织的数据）.
  特征匹配（feature matching， 用特征做为特征），只有下面两种方法：

  brute force matching （强制匹配）
  kd-tree nearest neighbor search (FLANN)（kd树最近邻搜索）.
  除了搜索法，还有两种著名对应估计：

  直接估计对应关系（默认），对点云A中的每一点，搜索在B中的对应关系
  “Reciprocal” 相互对应关系估计，只用A，B重叠部分，先从A到B找对应，再从B到A找对应。
  Correspondences rejection（剔除错误估计）
  剔除错误估计，可用 RANSAC 算法，或减少数量，只用一部分对应关系。有一种特殊的一到多对应，即模型中一个点对应源中的一堆点。这种情况可以用最短路径对应或检查附近的其他匹配过滤掉。

  Transformation estimation（最后一步，计算变换）
  基于上述匹配评估错误测量值；
  评估相机不同pose之间所作的刚性变换（运动估计），使错误测量值最小化；
  优化点云结构；
  E.g, - SVD 运动估计; - Levenberg-Marquardt用不同内核作运动估计；
  用刚性变换旋转/平移源数据到目标位置，可能需要对所有点/部分点/关键点内部运行ICP迭代循环；
  迭代，直到满足某些收敛标准。
  匹配流程总结