337专题

代码随想录Day39：198.打家劫舍、213.打家劫舍II、337.打家劫舍III

198. 打家劫舍题目链接：LeetCode198.打家劫舍文档讲解：代码随想录LeetCode198.打家劫舍题解 dp[i]偷或不偷，取决于dp[i-1]和dp[i-2]是否偷 class Solution {public:int rob(vector<int>& nums) {if (nums.size() == 1)return nums[0];vector<i

代码随想录算法训练营第三十九天 | 198.打家劫舍， 213.打家劫舍II ， 337.打家劫舍III

目录 198.打家劫舍思路 1.确定dp数组（dp table）以及下标的含义 2.确定递推公式 3.dp数组如何初始化 4.确定遍历顺序 5.举例推导dp数组方法一：动态规划-一维方法二：动态规划-二维方法三：动态规划-两个变量 213.打家劫舍II 思路方法一：动态规划- 方法二：动态规划-二维方法三：动态规划-不封装函数 337.打家劫舍III

【代码随想录训练营第42期 Day39打卡 - 打家劫舍问题 - LeetCode 198.打家劫舍 213.打家劫舍II 337.打家劫舍III

目录一、做题心得二、题目与题解题目一：198.打家劫舍题目链接题解：动态规划题目二：213.打家劫舍II 题目链接题解：动态规划题目三：337.打家劫舍III 题目链接题解：动态规划三、小结一、做题心得今天是打家劫舍的一天，来到了动态规划章节的Part7。打家劫舍问题是动态规划算法很经典的一个应用，今天将从三道题目对其进行探讨。

24暑假算法刷题 | Day39 | 动态规划 VII | LeetCode 198. 打家劫舍，213. 打家劫舍 II，337. 打家劫舍 III

目录 198. 打家劫舍题目描述题解 213. 打家劫舍 II题目描述题解 337. 打家劫舍 III题目描述题解打家劫舍的一天 😈 198. 打家劫舍点此跳转题目链接题目描述你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动

leetcode刷题（94）——337. 打家劫舍 III

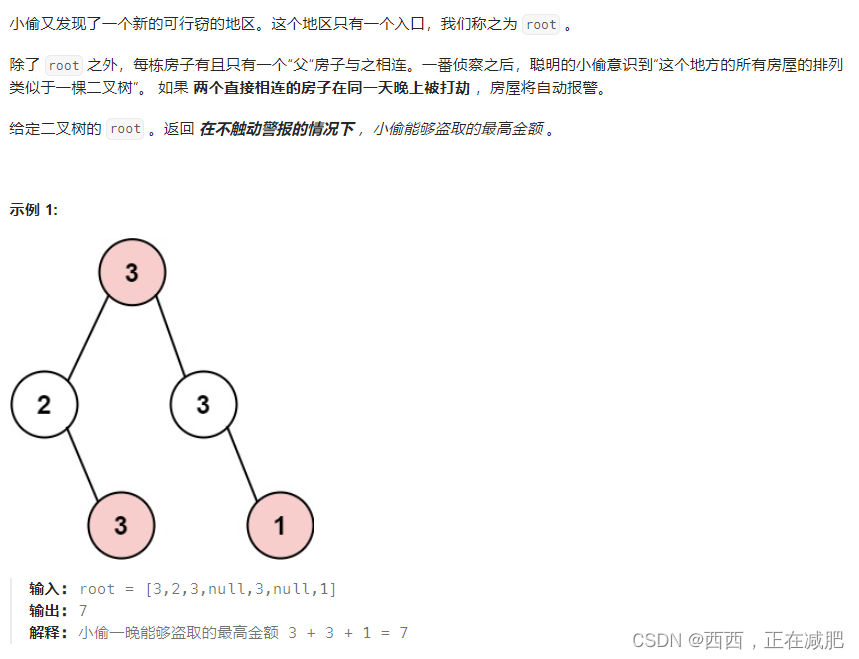
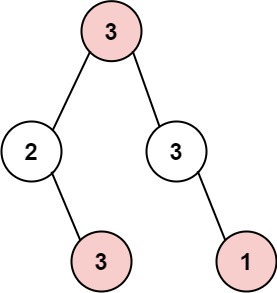
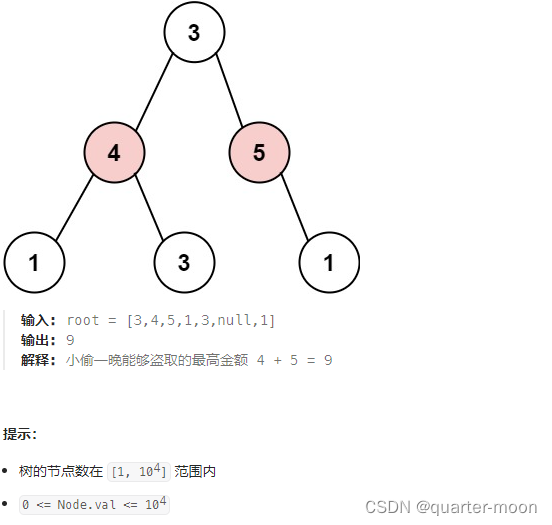
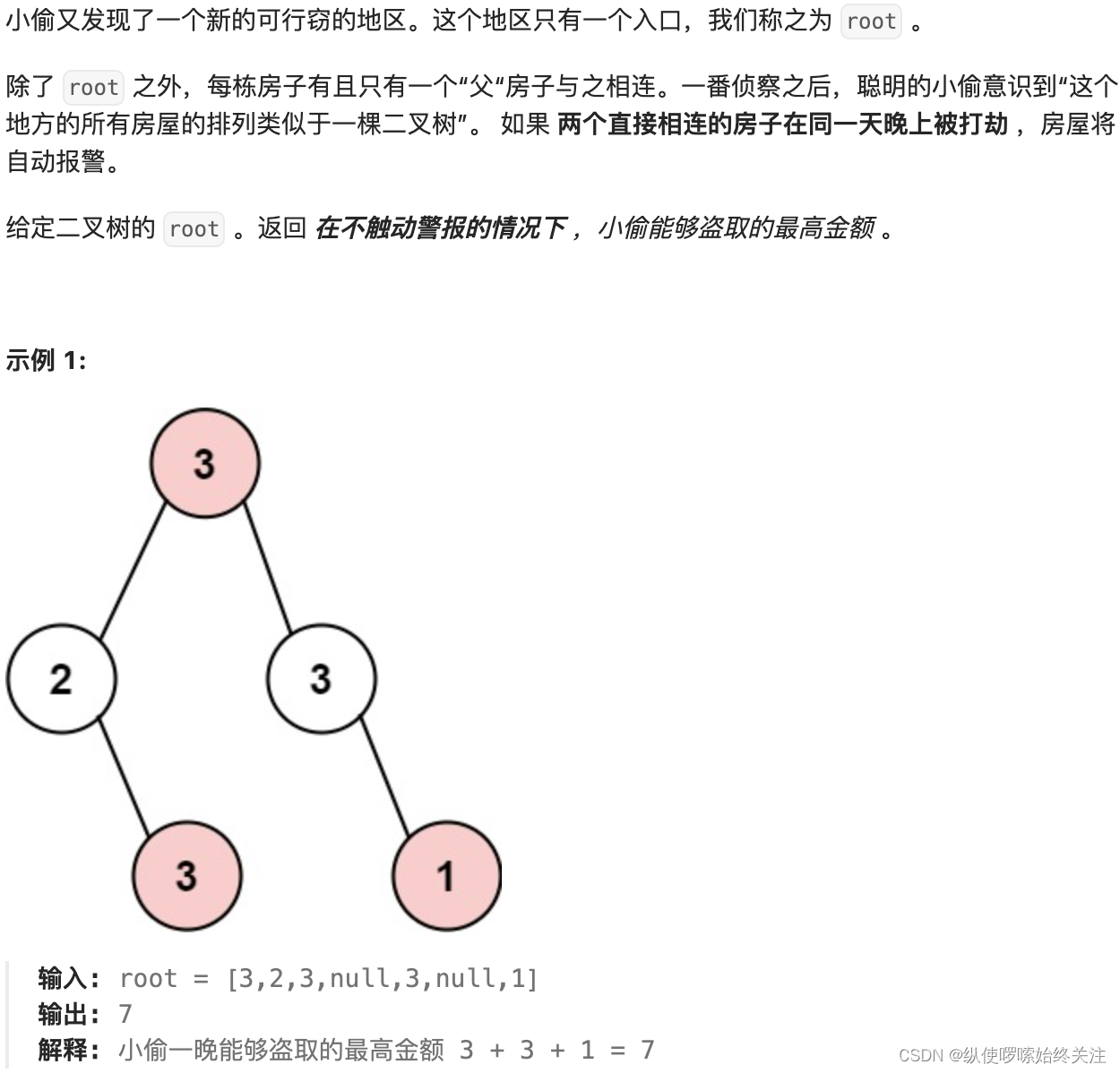
在上次打劫完一条街道之后和一圈房屋后，小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为“根”。除了“根”之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。如果两个直接相连的房子在同一天晚上被打劫，房屋将自动报警。计算在不触动警报的情况下，小偷一晚能够盗取的最高金额。示例 1: 输入: [3,2,

算法训练 | 动态规划Part7 | 198.打家劫舍、213.打家劫舍II、337.打家劫舍III

目录 198.打家劫舍（线性）动态规划法 213.打家劫舍II（环形）动态规划法 337.打家劫舍III（二叉树）动态规划法 198.打家劫舍（线性）题目链接：198. 打家劫舍 - 力扣（LeetCode）文章讲解：代码随想录动态规划法解题思路当前房屋偷与不偷取决于前一个房屋和前两个房屋是否被偷了。所以这里就更感觉到，当前状态和前面状态会有

代码随想录算法训练营第45天 [ 198.打家劫舍 213.打家劫舍II 337.打家劫舍III ]

代码随想录算法训练营第45天 [ 198.打家劫舍 213.打家劫舍II 337.打家劫舍III ] 一、198.打家劫舍链接: 代码随想录. 思路： dp[i]表示偷第i间房能获得的最大价值为dp[i] dp[0] = nums[0] dp[1] = max(nums[0],nums[1]) dp[i] = max(dp[i-2]+nums[i],dp[i-1]) 做题状态：看解析后

代码随想录算法训练营Day45|198.打家劫舍I、213.打家劫舍II、337.打家劫舍III

打家劫舍I 198. 打家劫舍 - 力扣（LeetCode）动态规划动态数组dp[i]表示在前i+1个房屋能偷到的最大金额。由于相邻不能偷的原则，dp[i] = max(dp[i-2]+nums[i],dp[i-1])，即为若要偷当前房屋，则比较前一个房屋dp[i-1]和不偷前一个房屋，但偷当前房屋的金额dp[i-2]+nums[i]的较大值。对dp数组的初始化，从dp数组的推导

代码随想录算法训练营第四十五天 | 198.打家劫舍、213.打家劫舍II、337.打家劫舍 III

198.打家劫舍题目链接：https://leetcode.cn/problems/house-robber/ 文档讲解：https://www.programmercarl.com/0198.%E6%89%93%E5%AE%B6%E5%8A%AB%E8%88%8D.html 视频讲解：https://www.bilibili.com/video/BV1Te411N7SX 思路确定

【代码随想录算法训练营第四十五天|198.打家劫舍、213.打家劫舍II、337.打家劫舍III】

文章目录 198.打家劫舍213.打家劫舍II337.打家劫舍III 198.打家劫舍 dp数组在这里是抢前i个房屋的最大受益，初始化头两个dp，推导的时候从前往后推，在前一位dp和前两位dp+现在的房子的受益中找最大值。（代码随想录里给了nums=[]，的判断其实不需要，leetcode上给出nums长度大于等于1了。 class Solution:def rob(self,

2024/06/18--代码随想录算法7/17|198.打家劫舍、213.打家劫舍II、337.打家劫舍III

198.打家劫舍力扣链接动态规划5步曲确定dp数组（dp table）以及下标的含义： dp[i]: 下标i内（包括i）的房屋，最多可以偷到的金额为dp[i]确定递推公式 dp[i] = max(dp[i-1], dp[i-2]+nums[i]）dp数组如何初始化 dp[0] = nums[0] dp[1]= max(nums[0], nums[1])确定遍历顺序:dp[i] 是根据

算法训练营第五十天 | LeetCode 198 打家劫舍、LeetCode 213 打家劫舍II、LeetCode 337 打家劫舍III

LeetCode 198 打家劫舍代码如下： class Solution {public:int rob(vector<int>& nums) {vector<int> dp(nums.size() + 1, 0);dp[1] = nums[0];for (int i = 2; i <= nums.size(); i++) {dp[i] = max(dp[i - 1] ,dp[i -

代码随想录训练营Day 50|力扣198.打家劫舍、213.打家劫舍II、337.打家劫舍III

1.打家劫舍视频讲解：动态规划，偷不偷这个房间呢？| LeetCode：198.打家劫舍_哔哩哔哩_bilibili 代码随想录代码： class Solution {public:int rob(vector<int>& nums) {if(nums.size() == 1) return nums[0];// dp数组定义及初始化vector<int> dp(nums

代码随想录Day 41|Leetcode|Python|198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III

198.打家劫舍你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你不触动警报装置的情况下，一夜之内能够偷窃到的最高金额。解题思路：确定dp数组含义：dp[i]遍历到房屋index为i时所能打劫到的

代码随想录算法训练营第四十八天| 198.打家劫舍，213.打家劫舍II，337.打家劫舍III

题目与题解 198.打家劫舍题目链接：198.打家劫舍代码随想录题解：198.打家劫舍视频讲解：动态规划，偷不偷这个房间呢？| LeetCode：198.打家劫舍_哔哩哔哩_bilibili 解题思路：这道还比较容易，设置dp[i]为偷到第i家的收益，那么，如果要偷第i家，就不偷第i-1家，收益为dp[i-2]+nums[i-1]；如果不偷第i家

【扩频通信】基于matlab扩频通信系统仿真【含Matlab源码 337期】

⛄一、获取代码方式获取代码方式1：完整代码已上传我的资源：【扩频通信】基于matlab扩频通信系统仿真【含Matlab源码 337期】点击上面蓝色字体，直接付费下载，即可。获取代码方式2：付费专栏Matlab信号处理（初级版）备注：点击上面蓝色字体付费专栏Matlab信号处理（初级版），扫描上面二维码，付费29.9元订阅海神之光博客付费专栏Matlab信号处理（初级版），凭支付

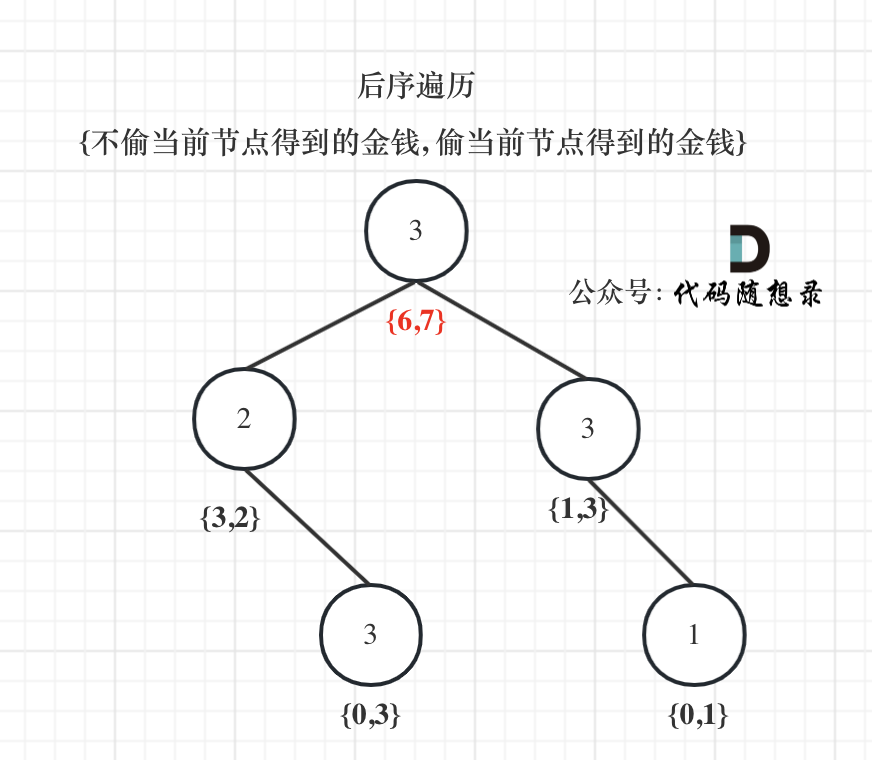
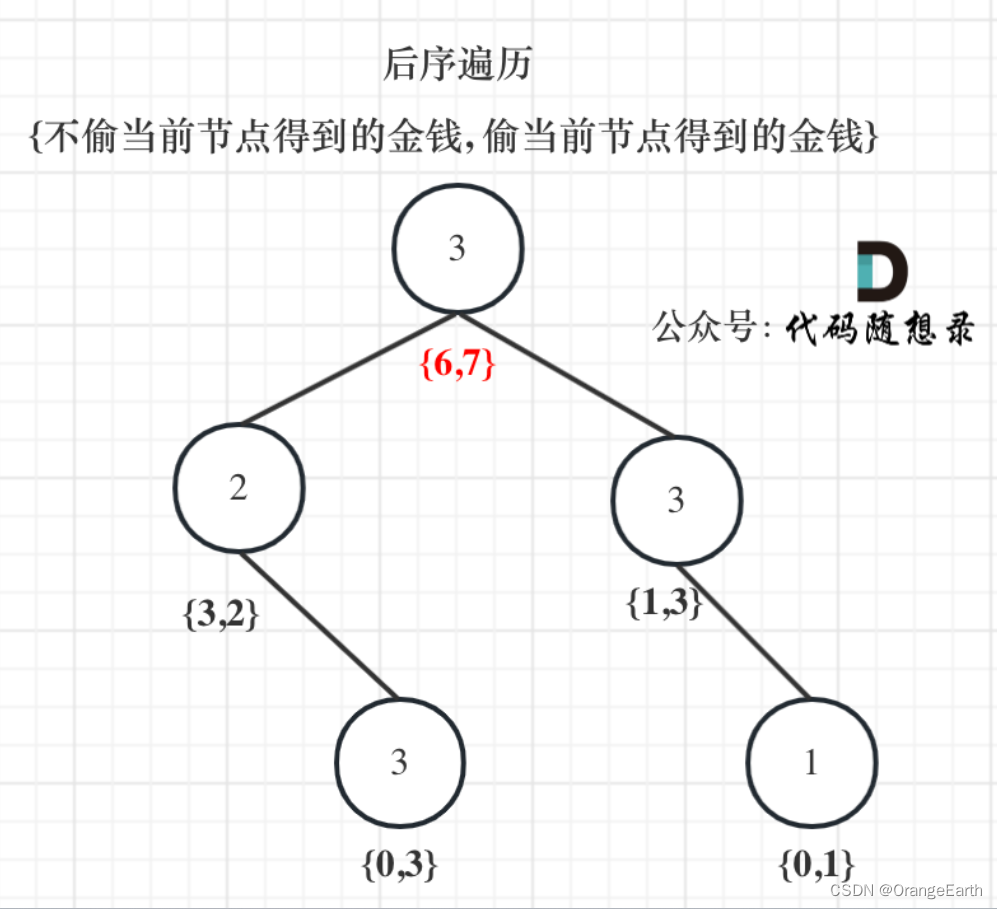
Leetcode 337 打家劫舍三 (树形dp)

// 经典树形dp// dp[i][0] 表示不抢i节点// dp[i][1] 表示抢i节点// dp[i][0] = max(dp[left][0], dp[left][1]) + max(dp[right][0], dp[right][1]);// dp[i][1] = nums[i] + dp[left][0] + dp[right][0];// 很好理解吧class Soluti

java算法day48 | 动态规划part09 ● 198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III

198.打家劫舍 class Solution {public int rob(int[] nums) {if(nums.length==0) return 0;if(nums.length==1) return nums[0];int[] dp=new int[nums.length];dp[0]=nums[0];dp[1]=Math.max(nums[1],nums[0]);for(i

【代码随想录算法训练营第四十八天 | LeetCode198.打家劫舍、213.打家劫舍II、337.打家劫舍III】

代码随想录算法训练营第四十八天 | LeetCode198.打家劫舍、213.打家劫舍II、337.打家劫舍III 一、198.打家劫舍解题代码C++： class Solution {public:int rob(vector<int>& nums) {if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[

刷题DAY48 | LeetCode 198-打家劫舍 213-打家劫舍II 337-打家劫舍III

198 打家劫舍（medium）你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你不触动警报装置的情况下，一夜之内能够偷窃到的最高金额。思路：动态规划法代码实现： class Solution

代码随想录算法训练营第四十七天|动态规划|198.打家劫舍、213.打家劫舍II、337.打家劫舍III

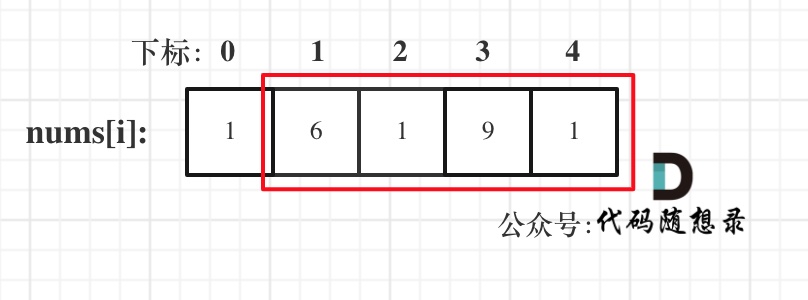
198.打家劫舍文章你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你不触动警报装置的情况下，一夜之内能够偷窃到的最高金额。示例 1：输入：[1,2,3,1] 输出：4 解释：偷窃 1 号房屋

代码随想录算法训练营day47|第九章动态规划part09：198.打家劫舍、213.打家劫舍II、337.打家劫舍III

目录打家劫舍是DP解决的经典题目，今天就是打家劫舍的一天，这个系列不算难，大家可以一口气拿下。 198.打家劫舍 213.打家劫舍II 337.打家劫舍III 198.打家劫舍视频讲解：动态规划，偷不偷这个房间呢？| LeetCode：198.打家劫舍_哔哩哔哩_bilibili 代码随想录首先，dp[i]表示考虑下标i（包括i）以内的房屋，最多可以偷窃的金额。如果

day48 ● 198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III

一遍过。当前房屋偷与不偷取决于前一个房屋和前两个房屋是否被偷了。所以这里就更感觉到，当前状态和前面状态会有一种依赖关系，那么这种依赖关系都是动规的递推公式。 class Solution {public:int rob(vector<int>& nums) {vector<vector<int>> dp(40001,vector<int>(2,0));for(int i=1;i<=n

代码随想录算法训练营第47天| 198.打家劫舍、213.打家劫舍II、337.打家劫舍III

198.打家劫舍完成思路：本题中，偷与不偷一个房间，与前两个房间的状态是相关的，可以用动态规划解题。 dp[i]代表能从0-i房间偷取的最大金额。对于每个房间而言，都有偷和不偷两种选择。如果偷这个房间，那么前一个房间就不能偷了，dp[i] = nums[i] + dp[i-2]；如果不偷这个房间，dp[i] = dp[i-1]。代码 class Solution {p

代码随想录算法训练营第52天（动态规划09 ● 198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III

动态规划part09 198.打家劫舍解题思路 213.打家劫舍II解题思路 337.打家劫舍III解题思路今天就是打家劫舍的一天，这个系列不算难，大家可以一口气拿下。 198.打家劫舍题目链接： 198.打家劫舍视频讲解： 198.打家劫舍文章讲解： 198.打家劫舍解题思路递归五部曲确定dp数组以及下标的含义 dp[i]：考虑下标i（包括

代码随想录算法训练营第52天 | 198.打家劫舍 213.打家劫舍II 337.打家劫舍 III

打家劫舍关键点在于当前的房屋偷不偷，这取决于前一个房子有没有被偷，在确保前一个房子不被偷可以偷一下当前的房子。 class Solution{public:int rob(vector<int>& nums) {if(nums.size() == 1) return nums[0];vector<int> dp(nums.size(), 0); // dp[i]表示偷下标i之前的房屋