代码随想录算法训练营第52天 | 198.打家劫舍 213.打家劫舍II 337.打家劫舍 III

本文主要是介绍代码随想录算法训练营第52天 | 198.打家劫舍 213.打家劫舍II 337.打家劫舍 III，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

打家劫舍

Alt
关键点在于当前的房屋偷不偷，这取决于前一个房子有没有被偷，在确保前一个房子不被偷可以偷一下当前的房子。

class Solution{
public:int rob(vector<int>& nums) {if(nums.size() == 1)  return nums[0];vector<int> dp(nums.size(), 0);  // dp[i]表示偷下标i之前的房屋能得到的最大价值dp[0] = nums[0];dp[1] = max(nums[0], nums[1]);for(int i = 2; i < nums.size(); i++) {// dp[i - 2]表示前一个房子不偷，那么就偷当前的房屋// dp[i - 1]表示可以偷前一个房子，不能偷当前的房屋dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);}return dp[nums.size() - 1];}
};

打家劫舍II

Alt
房子连成了环，偷第一个房间就不能偷最后一个房间。所以我们就可以从两个方面考虑问题，考虑不含最后一个房屋的序列与考虑不含第一个房屋的序列，取两种情况的最大值，就是最终的最高金额。

class Solution{
public:int robRange(vector<int>& nums, int start, int end){vector<int> dp(nums.size(), 0);  // 仍然创建nums.size()大小的dp数组dp[start] = nums[start];  // 注意这里dp的下标是start，不是0dp[start + 1] = max(nums[start], nums[start + 1]);for(int i = start + 2; i <= end; i++) {dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);}return dp[end];}int rob(vector<int>& nums) {if(nums.size() == 1)  return nums[0];if(nums.size() == 2)  return max(nums[0], nums[1]);int result1 = robRange(nums, 0, nums.size() - 2);int result2 = robRange(nums, 1, nums.size() - 1);return max(result1, result2);}
};

打家劫舍III

Alt
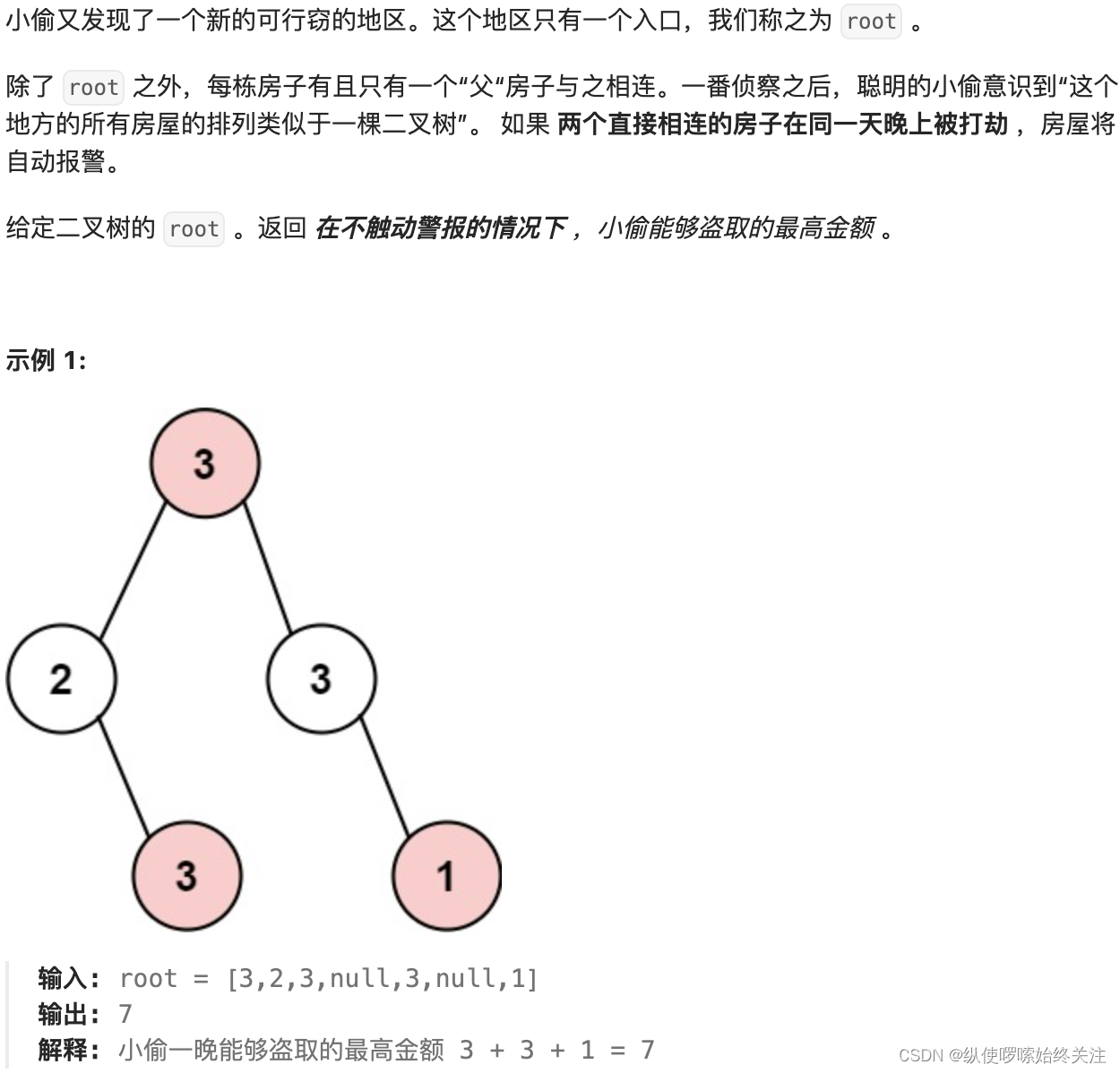
涉及到树的问题，确定遍历顺序是必要的，我们需要用递归的返回值来确定当前的节点的值。与前面的打家劫舍问题类似，就是偷不偷当前的节点，如果要偷当前的节点，左右孩子节点都不能偷；如果不偷当前的节点，那么就要考虑偷左右孩子节点。
记忆化递归：

class Solution{
public:unordered_map<TreeNode*, int> umap;int rob(TreeNode* root) {if(root == NULL)  return 0;  // 当前节点是空，偷不偷都只能得到0if(root->left == NULL && root->right == NULL)  return root->val;if(umap[root])  return umap[root];  // 如果不记忆化搜索，孙子节点会被反复计算int val1 = root->val;  // 偷当前的节点if(root->left)  val1 += rob(root->left->left) + rob(root->left->right);if(root->right)  val1 += rob(root->right->left) + rob(root->right->right);int val2 = rob(root->left) + rob(root->right);  // 不偷当前节点，考虑偷叶子节点umap[root] = max(val1, val2);return max(val1, val2);}
};

树形dp
设计dp数组的长度为2，第一维是不偷当前节点获得的金额，第二维是偷当前节点的金额。这里要注意二叉树的后序遍历与dp数组的状态转移。

class Solution {
public:int rob(TreeNode* root) {vector<int> result = robTree(root);return max(result[0], result[1]);}vector<int> robTree(TreeNode* cur) {if(cur == NULL)  return vector<int>{0, 0};vector<int> left = robTree(cur->left);vector<int> right = robTree(cur->right);vector<int> dp(2, 0);  // 0-不偷当前节点；1-偷当前节点dp[0] = max(left[0], left[1]) + max(right[0], right[1]);dp[1] = cur->val + left[0] + right[0];return dp;}
};