213专题

[LeetCode] 213. House Robber II

题：https://leetcode.com/problems/house-robber-ii/description/ 题目 You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at t

leetcode解题思路分析（二十九）207—213题

课程表你这个学期必须选修 numCourse 门课程，记为 0 到 numCourse-1 。在选修某些课程之前需要一些先修课程。例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们：[0,1] 给定课程总量以及它们的先决条件，请你判断是否可能完成所有课程的学习？本题可以采取DFS，如果找到了环路则证明不可以，否则可以 const int maxn=1000050

反射机制_提高反射效率_操作泛型_操作注解JAVA213

来源：http://www.bjsxt.com/ 一、S02E213反射机制_提高反射效率、操作泛型、操作注解反射机制性能问题 package com.test.reflection;import java.lang.reflect.InvocationTargetException;import java.lang.reflect.Method;import com.test.be

LeetCode讲解篇之213. 打家劫舍 II

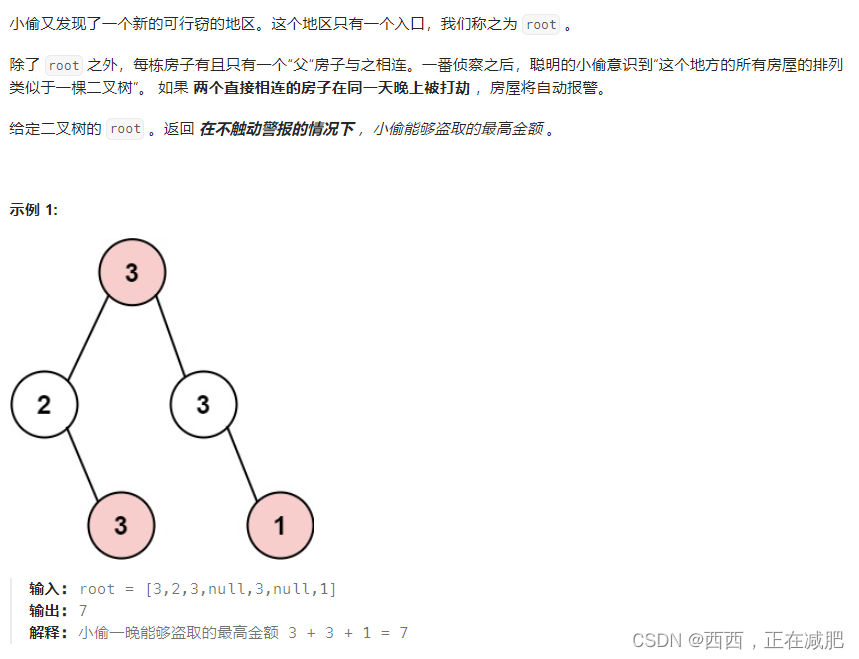
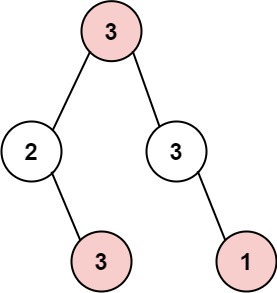
文章目录题目描述题解思路题解代码题目描述你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，今晚能够偷

HLS报错之：Export RTL报错 “ERROR: [IMPL 213-28] Failed to generate IP.“

原因：官方bug 解决办法：下载补丁（补丁适用于2014年至2021年的多个Vivado版本），并添加到对应路径下即可。注意：windows下该方法试用。补丁连接我这里下载到xilinx的目录下并解压：点进去找到该文件：复制到scripts路径下即可现在export RTL就正常了

基于STM32设计的智能饮水机_升级版(微信小程序)(213)

文章目录一、前言1.1 项目介绍【1】项目功能介绍【2】设计实现的功能【3】项目硬件模块组成 1.2 设计思路【1】整体设计思路【2】ESP8266工作模式配置 1.3 项目开发背景【1】选题的意义【2】可行性分析【3】参考文献【4】摘要【5】选题背景【6】国内外技术发展现状 1.4 开发工具的选择【1】设备端开发【2】上位机开发 1.5 系统框架图1.6 系统功能总结1.7 系统原理图1

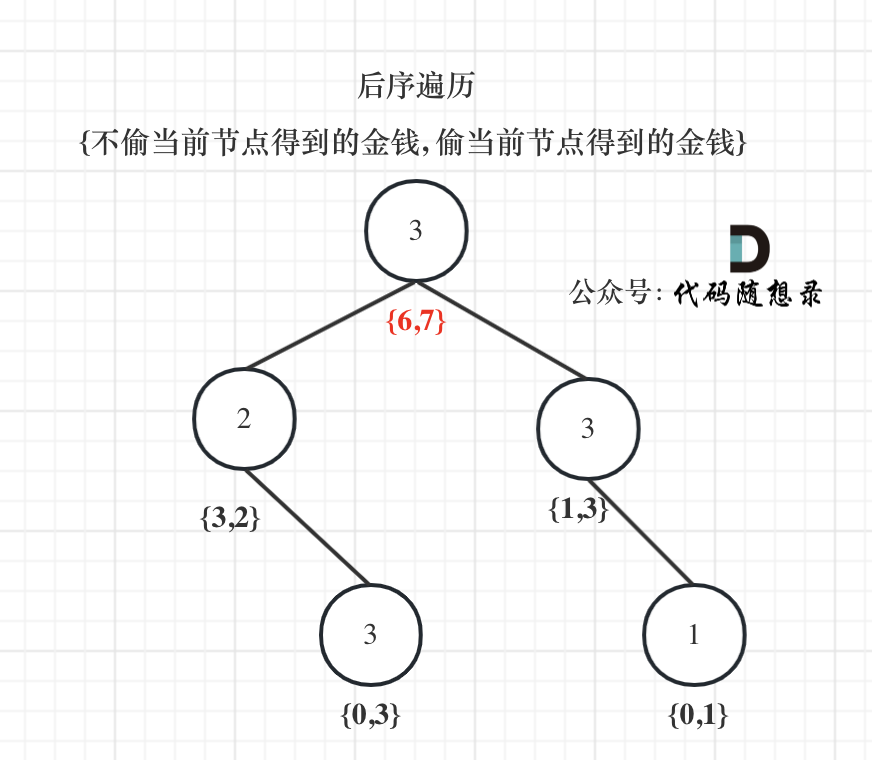
代码随想录Day39：198.打家劫舍、213.打家劫舍II、337.打家劫舍III

198. 打家劫舍题目链接：LeetCode198.打家劫舍文档讲解：代码随想录LeetCode198.打家劫舍题解 dp[i]偷或不偷，取决于dp[i-1]和dp[i-2]是否偷 class Solution {public:int rob(vector<int>& nums) {if (nums.size() == 1)return nums[0];vector<i

代码随想录算法训练营第三十九天 | 198.打家劫舍， 213.打家劫舍II ， 337.打家劫舍III

目录 198.打家劫舍思路 1.确定dp数组（dp table）以及下标的含义 2.确定递推公式 3.dp数组如何初始化 4.确定遍历顺序 5.举例推导dp数组方法一：动态规划-一维方法二：动态规划-二维方法三：动态规划-两个变量 213.打家劫舍II 思路方法一：动态规划- 方法二：动态规划-二维方法三：动态规划-不封装函数 337.打家劫舍III

【代码随想录训练营第42期 Day39打卡 - 打家劫舍问题 - LeetCode 198.打家劫舍 213.打家劫舍II 337.打家劫舍III

目录一、做题心得二、题目与题解题目一：198.打家劫舍题目链接题解：动态规划题目二：213.打家劫舍II 题目链接题解：动态规划题目三：337.打家劫舍III 题目链接题解：动态规划三、小结一、做题心得今天是打家劫舍的一天，来到了动态规划章节的Part7。打家劫舍问题是动态规划算法很经典的一个应用，今天将从三道题目对其进行探讨。

24暑假算法刷题 | Day39 | 动态规划 VII | LeetCode 198. 打家劫舍，213. 打家劫舍 II，337. 打家劫舍 III

目录 198. 打家劫舍题目描述题解 213. 打家劫舍 II题目描述题解 337. 打家劫舍 III题目描述题解打家劫舍的一天 😈 198. 打家劫舍点此跳转题目链接题目描述你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动

leetcode刷题（93）——213. 打家劫舍 II

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。示例 1: 输入: [2,3,2]输出: 3解释:

算法训练 | 动态规划Part7 | 198.打家劫舍、213.打家劫舍II、337.打家劫舍III

目录 198.打家劫舍（线性）动态规划法 213.打家劫舍II（环形）动态规划法 337.打家劫舍III（二叉树）动态规划法 198.打家劫舍（线性）题目链接：198. 打家劫舍 - 力扣（LeetCode）文章讲解：代码随想录动态规划法解题思路当前房屋偷与不偷取决于前一个房屋和前两个房屋是否被偷了。所以这里就更感觉到，当前状态和前面状态会有

代码随想录算法训练营第45天 [ 198.打家劫舍 213.打家劫舍II 337.打家劫舍III ]

代码随想录算法训练营第45天 [ 198.打家劫舍 213.打家劫舍II 337.打家劫舍III ] 一、198.打家劫舍链接: 代码随想录. 思路： dp[i]表示偷第i间房能获得的最大价值为dp[i] dp[0] = nums[0] dp[1] = max(nums[0],nums[1]) dp[i] = max(dp[i-2]+nums[i],dp[i-1]) 做题状态：看解析后

代码随想录算法训练营Day45|198.打家劫舍I、213.打家劫舍II、337.打家劫舍III

打家劫舍I 198. 打家劫舍 - 力扣（LeetCode）动态规划动态数组dp[i]表示在前i+1个房屋能偷到的最大金额。由于相邻不能偷的原则，dp[i] = max(dp[i-2]+nums[i],dp[i-1])，即为若要偷当前房屋，则比较前一个房屋dp[i-1]和不偷前一个房屋，但偷当前房屋的金额dp[i-2]+nums[i]的较大值。对dp数组的初始化，从dp数组的推导

代码随想录算法训练营第四十五天 | 198.打家劫舍、213.打家劫舍II、337.打家劫舍 III

198.打家劫舍题目链接：https://leetcode.cn/problems/house-robber/ 文档讲解：https://www.programmercarl.com/0198.%E6%89%93%E5%AE%B6%E5%8A%AB%E8%88%8D.html 视频讲解：https://www.bilibili.com/video/BV1Te411N7SX 思路确定

【代码随想录算法训练营第四十五天|198.打家劫舍、213.打家劫舍II、337.打家劫舍III】

文章目录 198.打家劫舍213.打家劫舍II337.打家劫舍III 198.打家劫舍 dp数组在这里是抢前i个房屋的最大受益，初始化头两个dp，推导的时候从前往后推，在前一位dp和前两位dp+现在的房子的受益中找最大值。（代码随想录里给了nums=[]，的判断其实不需要，leetcode上给出nums长度大于等于1了。 class Solution:def rob(self,

2024/06/18--代码随想录算法7/17|198.打家劫舍、213.打家劫舍II、337.打家劫舍III

198.打家劫舍力扣链接动态规划5步曲确定dp数组（dp table）以及下标的含义： dp[i]: 下标i内（包括i）的房屋，最多可以偷到的金额为dp[i]确定递推公式 dp[i] = max(dp[i-1], dp[i-2]+nums[i]）dp数组如何初始化 dp[0] = nums[0] dp[1]= max(nums[0], nums[1])确定遍历顺序:dp[i] 是根据

算法训练营第五十天 | LeetCode 198 打家劫舍、LeetCode 213 打家劫舍II、LeetCode 337 打家劫舍III

LeetCode 198 打家劫舍代码如下： class Solution {public:int rob(vector<int>& nums) {vector<int> dp(nums.size() + 1, 0);dp[1] = nums[0];for (int i = 2; i <= nums.size(); i++) {dp[i] = max(dp[i - 1] ,dp[i -

代码随想录训练营Day 50|力扣198.打家劫舍、213.打家劫舍II、337.打家劫舍III

1.打家劫舍视频讲解：动态规划，偷不偷这个房间呢？| LeetCode：198.打家劫舍_哔哩哔哩_bilibili 代码随想录代码： class Solution {public:int rob(vector<int>& nums) {if(nums.size() == 1) return nums[0];// dp数组定义及初始化vector<int> dp(nums

动态规划-leetcode#213 打家劫环形舍

这题与leetcode#198相似，只是升级为环形房屋，也就是第一个和最后一个也是相邻的。回顾一下简单版解决方案： class Solution {//leetcode#198代码public:int rob(vector<int>& nums) {if(nums.empty()) return 0;vector<int> dp(nums.size(),0);dp[0]=nums[0];for

LeetCode 题解(213) : Peeking Iterator

题目： Given an Iterator class interface with methods: next() and hasNext(), design and implement a PeekingIterator that support the peek() operation -- it essentially peek() at the element that will

hdu 4810 思维题+二进制位规律+异或规律 213南京现场赛题

http://acm.hdu.edu.cn/showproblem.php?pid=4810 以前做过一些涉及异或的题，化为二进制形式，然后统计0,1个数是一种很常见的处理方法，但是在做这个题的时候居然没尝试，脑残啊...... 一开始看5s时限，感觉稍微暴力一点应该可以，于是YY的O(n^3)算法但是没去实现，明显超时啊，大致就是通过C(n,1)的组合可以在O(n^2)内处理出C(n,2)的

代码随想录算法训练营DAY47|C++动态规划Part8|198.打家劫舍、213.打家劫舍II、198.打家劫舍III

文章目录 198.打家劫舍思路CPP代码 ⭐️213.打家劫舍II解决环的问题思路总结CPP代码 ⭐️198.打家劫舍III思路递归三部曲——确定参数和返回值递归三部曲——确定终止条件递归三部曲——确定单层遍历的逻辑打印dp数组CPP代码暴力递归记忆化递归 198.打家劫舍力扣题目链接文章讲解：198.打家劫舍视频讲解：动态规划，偷不偷这个房间呢？| LeetCode

代码随想录Day 41|Leetcode|Python|198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III

198.打家劫舍你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你不触动警报装置的情况下，一夜之内能够偷窃到的最高金额。解题思路：确定dp数组含义：dp[i]遍历到房屋index为i时所能打劫到的

每日一题(力扣213)：打家劫舍2--dp+分治

与打家劫舍1不同的是它最后一个和第一个会相邻，事实上，从结果思考，最后只会有三种：1 第一家不被抢最后一家被抢 2 第一家被抢最后一家不被抢 3 第一和最后一家都不被抢。那么，根据打家劫舍1中的算法我们能算出在i到j房子区间内能抢到的最大金额，那我们可以考虑计算两路 1 从1 到 n-1的结果和从 2 到 n的结果，最后取两者的最大即可。（第一家和最后一家都没被抢的情况实际

LeetCode 213 —— 打家劫舍 II

阅读目录 1. 题目2. 解题思路3. 代码实现 1. 题目 2. 解题思路此题是 LeetCode 198—— 打家劫舍的升级版，多了一个首尾相连的设定。因为首尾相连，所以第一个房屋和最后一个房屋只能偷窃其中一个。所以，第一种方案就是不偷窃最后一个房屋，那么我们从第一个房屋偷到倒数第二个房屋，看看这样能偷窃到的最大值是什么。第二种方案则是从最后一个房屋偷