随机变量专题
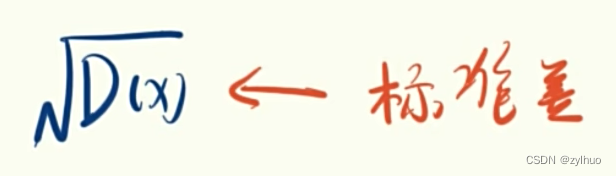
概率学 笔记一 - 概率 - 随机变量 - 期望 - 方差 - 标准差(也不知道会不会有二)
概率不用介绍,它的定义可以用一个公式写出: 事件发生的概率 = 事件可能发生的个数 结果的总数 事件发生的概率=\cfrac{事件可能发生的个数}{结果的总数} 事件发生的概率=结果的总数事件可能发生的个数 比如一副标准的 52 张的扑克牌,每张牌都是唯一的,所以,抽一张牌时,每张牌的概率都是 1/52。但是有人就会说了,A 点明明有四张,怎么会是 1/52 的概率。 这就需要精准的指出
概率论(三)-多维随机变量及其分布:n维随机变量、概率分布函数F(x1,x2,..xn)、联合分布律、联合概率密度、边缘分布律、边缘概率密度、条件分布律、条件概率密度、β函数、Γ函数、max{X,Y}
1 二维随机变量 2 边缘分布 3 条件分布 4 相互独立的随机变量 5 两个随机变量的函数的分布
概率论(二)-随机变量及其分布:分布函数F(x)、离散型随机变量【分布律:(0-1)分布、二项分布、泊松分布】、连续型随机变量【概率密度:均匀分布、指数分布、正态/高斯分布】、3σ法则、偏度、峰度
1 随机变量 2 离散型随机变量及其分布律 3 随机变量的分布函数 4 连续型随机变量及其概率密度 5 随机变量的函数的分布
随机变量和随机变量序列是什么关系
随机序列的定义 随机序列(random sequence),更确切 的,应该叫做,随机变量序列。随机变量序列,也就是随机变量形成的序列。有时候为了简称,省略了变量二字。 随机变量:表示随机现象(在一定条件下,并不总是出现相同结果的现象称为随机现象)各种结果的变量(一切可能的样本点)。随机序列:随机序列的产生为了形容随机变量形成的序列。 一般的,如果用X1,X2……Xn(表示n下标于X)代表随机变
[概率论]-离散型随机变量·二项分布
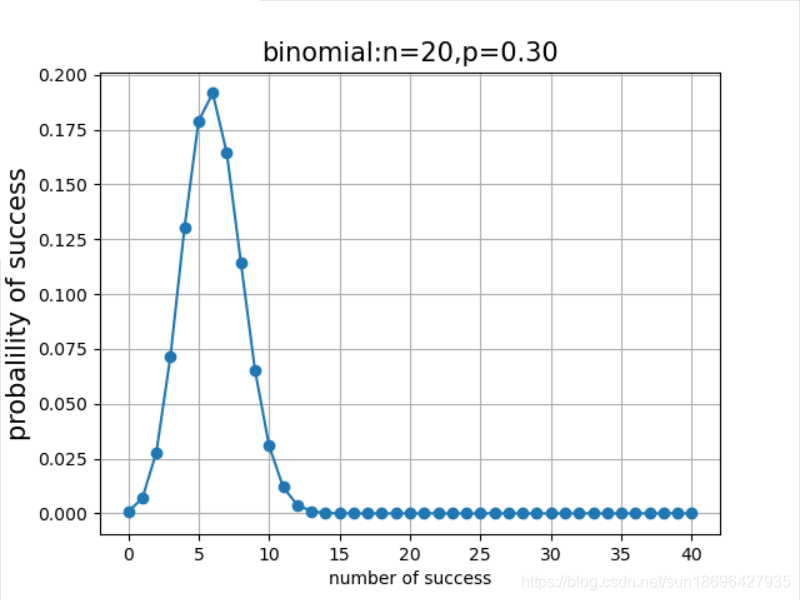
离散型随机变量 设X是一个随机变量,如果它全部可能的取值只有有限个或可数无穷个,则称X为一个离散型随机变量。 二项分布 伯努利实验 伯努利试验(Bernoulli experiment)是在同样的条件下重复地、相互独立地进行的一种随机试验,其特点是该随机试验只有两种可能结果:发生或者不发生。我们假设该项试验独立重复地进行了n次,那么就称这一系列重复独立的随机试验为n重伯努利试验,或称为伯努
概率统计Python计算:连续型随机变量分布(norm)
scipy.stats的norm对象表示正态分布,下表说明norm的几个常用函数。 函数名参数功能rvs(loc, scale, size)loc,scale:分布参数 μ \mu μ和 σ \sigma σ,缺省值分别为0和1,size:产生的随机数个数,缺省值为1产生size个随机数pdf(x, loc, scale)x:自变量取值,loc,scale:与上同概率密度函数 f ( x )
概率统计Python计算:连续型随机变量分布(uniform expon)
1. uniform分布(均匀分布) Python的scipy.stats包中的对象uniform表示连续型的均匀分布。下表展示了uniform分布的几个常用函数。 函数名参数功能rvs(loc, scale, size)loc:分布参数 a a a,缺省值为0, scale:分布参数差 b − a b-a b−a,缺省值为1,size:产生的随机数个数,缺省值为1产生size个随机数pd
概率统计Python计算:离散型随机变量分布(bernoulli geom)
Python的scipy.stats包中提供了各种随机变量的分布。每一种分布,其累积分布函数(分布函数)记为cdf。离散型变量分布的概率质量函数(分布律),记为pmf。除此之外,每个分布都有一个服从该分部变量发生器函数rvs,用来产生服从该分布的随机数。 1. bernoulli分布(0-1分布) Python的scipy.stats包中,bernoulli类就是用来表示伯努利分布的。常用的
概率统计Python计算:随机变量的分布函数
任何随机变量 X X X都有其分布函数(或称为累积分布函数) F ( x ) = P ( X ≤ x ) , x ∈ ( − ∞ , + ∞ ) . F(x)=P(X\leq x), x\in (-\infty,+\infty). F(x)=P(X≤x),x∈(−∞,+∞). 例1 向半径为 r r r的圆内任一投掷一个点,求此点到圆心的距离 X X X的分布函数,并计算 P ( X > r
引入分布函数和概率密度函数解释:三种常见连续型随机变量的分布(均匀、指数、正态)
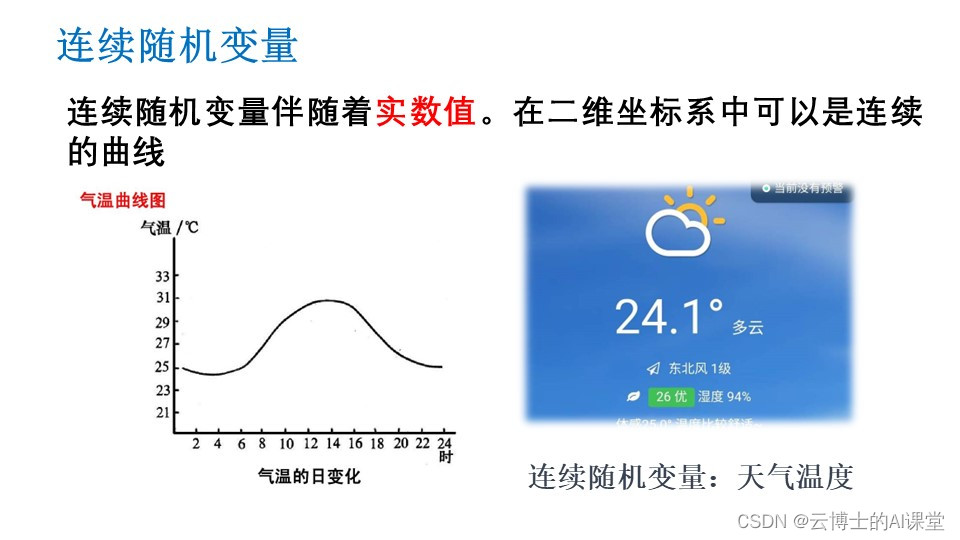
连续性随机变量及其分布 在概率论和统计学中,我们常常会接触到连续性随机变量及其分布。连续性随机变量的一个显著特征是其取值可以在一个连续的范围内变化,比如温度、身高、体重等。为了更好地理解和分析这些随机变量,我们需要使用分布函数和概率密度函数。 分布函数和概率密度函数 **分布函数(Cumulative Distribution Function, CDF)**是描述一个随机变量取值小于或等于
AI学习指南概率论篇-随机变量和随机过程
AI学习指南概率论篇-随机变量和随机过程 随机变量和随机过程是概率论中重要的概念,也是在人工智能领域中经常应用的概念。本文将介绍随机变量和随机过程的概述,它们在AI中的使用场景,定义和意义,以及相关的公式讲解,并提供详细的示例。 概述 随机变量是描述随机现象结果的变量,它可以是离散的也可以是连续的。在概率论和统计学中,我们常常用随机变量来描述事件的发生概率。 随机过程是一种随机现象随时间变
AI-数学-高中52-离散型随机变量概念及其分布列、两点分布
原作者视频:【随机变量】【一数辞典】2离散型随机变量及其分布列_哔哩哔哩_bilibili 离散型随机变量分布列:X表示离散型随机变量可能在取值,P:对应分布在概率,P括号里X=1表示事件的名称。 示例:
【概率论】4-1:随机变量的期望(The Expectation of a Random Variable Part II)
原文地址1:https://www.face2ai.com/Math-Probability-4-1-The-Expectation-of-a-Random-Variable-P2转载请标明出处 Abstract: 本篇介绍期望的第二部分,关于随机变量的函数的期望 Keywords: Expectation 随机变量的期望 本来这篇可以和前一篇合在一起的,但是看了下还是有点长,控制下篇幅来保证
【概率论】4-1:随机变量的期望(The Expectation of a Random Variable Part I)
原文地址1:https://www.face2ai.com/Math-Probability-4-1-The-Expectation-of-a-Random-Variable-P1转载请标明出处 Abstract: 本文主要介绍期望的基础之知识,第一部分介绍连续和离散随机变量的期望。 Keywords: Expectation 随机变量的期望 好像大家比较喜欢关于学习方面的废话,那么以后就不说
CDF与PDF(描述随机变量的分布情况)
一、概念解释 CDF(Cumulative Distribution Function)和PDF(Probability Density Function)是概率论和统计学中常用的两个评价指标,用于描述随机变量的分布情况。 1. CDF(累积分布函数): - CDF是描述随机变量在某个取值及其之前所有可能取值的概率的函数。它表示了累积概率,即随机变量取值小于或等于某一给定值的概率。 - 数
c语言随机变量输出,Arduino 如何输出变量 像c语言那样 printf(%d,n)这样在液晶屏上输出随机变...
满意答案 倚楼听雨_____ 2016.12.15 采纳率:44% 等级:8 已帮助:662人 不同接口类型的LCD屏需要不同的库,如我用IIC接口的1602,使用#include ,程序中定义 //使用IIC总线定义LCD地址0X27,16字符2行 LiquidCrystal_I2C lcd(0x27, 16, 2); 之后就可以 lcd.clear(); lcd.print("TS
MMSE估计(一):连续随机变量的估计
【本文内容摘自"Signals, Systems and Inferences"之"8.1-Estimation of a Continuous Random Variable", by Alan V.Oppenheim and George C.Verghese, 2010.】 连续随机变量的MMSE估计 首先,我们假定对随机变量 Y Y Y感兴趣想要估计它的值,但我们只知道它的概率密度函
离散型随机变量及其常见分布律
文章目录 1. 随机变量2. 离散型随机变量3. 离散型随机变量常见分布3.1 ( 0 − 1 ) (0-1) (0−1)分布3.2 二项分布3.3 泊松分布3.4 几何分布3.5 超几何分布 1. 随机变量 设随机试验的样本空间为 S = { e } S=\{e\} S={e}. X = X ( e ) X=X(e) X=X(e) 是定义在样本空间 S S S上的
概率论与数理统计————3.随机变量及其分布
一、随机变量 设E是一个随机试验,S为样本空间,样本空间的任意样本点e可以通过特定的对应法则X,使得每个样本点都有与之对应的数对应,则称X=X(e)为随机变量 二、分布函数 分布函数:设X为随机变量,x是任意实数,则事件{Xx}为随机变量X的分布函数,记为F(x) 即:F(x)=P(Xx) (1)几何意义: (2)某点处的概率:P(a)=P(Xa)-P(X<a) 性