随机事件与随机变量

本文主要是介绍随机事件与随机变量，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

⼀、随机事件

1、随机事件基本概念

事例引入：
现有一枚普通形状的骰子，将骰子连续投5次，每次投掷出的结果可能性是均等的
其中：
1、投掷骰子并得出均等结果的行为称作随机现象
2、投掷骰子所能得出所有结果的集合称为样本空间
3、投掷骰子所得出的每一个结果称为样本点
4、投掷骰子所得出的结果都在1-6之间，称为必然事件
5、投掷骰子所得出的结果不在1-6之间，则称为不可能事件
6、投掷骰子所得出的某个结果的可能性，则称为概率
其余必须了解的知识点：
1、随机试验需要满足三个条件
2、概率的定义与主要性质

2、古典概型

定义：每个样本点出现时等可能的，并且每次试验有且仅有一个样本点发生，则称这类现象为古典概型
重要知识点：排列组合公式的使用（重复或非重复行为）
例1：生日问题
假若一个班上共有40名学生，一年按365天计算的话，该班没有两人生日相同的概率

#我们采⽤用函数的递归的⽅方法计算阶乘：
def factorial(n):if n == 0:return 1else:return (n*factorial(n-1))
l_fac = factorial(365); #l的阶乘
l_k_fac = factorial(365-40) #l-k的阶乘
l_k_exp = 365**40 #l的k次⽅方
P_B = l_fac /(l_k_fac * l_k_exp) #P(B）
print("事件B的概率为：",P_B)
print("40个同学中⾄至少两个⼈人同⼀一天过⽣生⽇日的概率是：",1 - P_B)

3、条件概率

定义：设A和B是两个事件，且P(B)>0,称P(A|B)=P(AB)/P(B)为在事件B发生的条件下，事件A发生的概率。
3、全概率公式与贝叶斯公式

二、随机变量

1、随机变量及其分布
2、离散型随机变量
3、常见的离散型分布：伯努利二项分布
4、随机变量的数字特征：数学期望定义与主要性质、方差定义与主要性质

三、练习

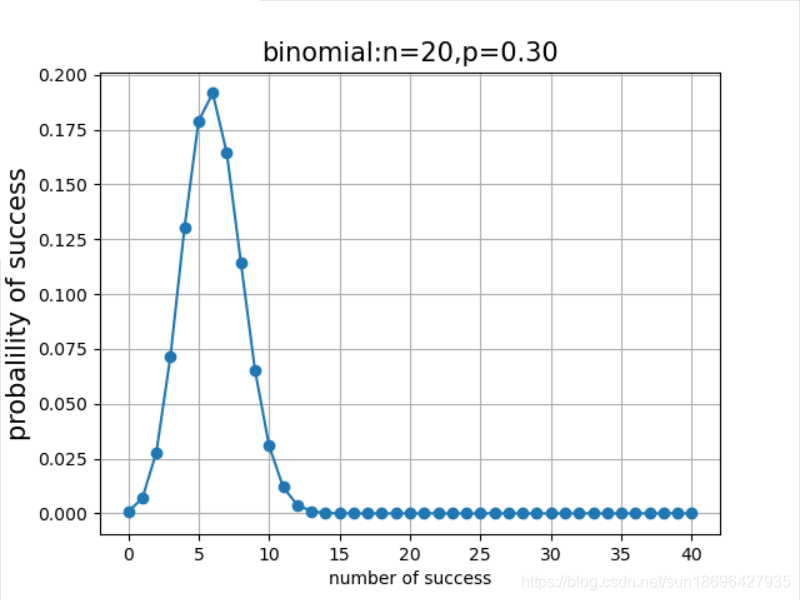
1、python实现二项分布

import numpy as np
import matplotlib.pyplot as plt
import math
from scipy import stats
n = 20
p = 0.3
k = np.arange(0,41)
print(k)
print("*"*20)
binomial = stats.binom.pmf(k,n,p)
print(binomial)
plt.plot(k, binomial, 'o-')
plt.title('binomial:n=%i,p=%.2f'%(n,p),fontsize=15)
plt.xlabel('number of success')
plt.ylabel('probalility of success', fontsize=15)
plt.grid(True)
plt.show()

2、表示出协方差和相关系数

#协方差
import numpy as np
arr = np.array([1,2,3,4])
print("Covariance: np.cov()", np.cov(arr))
#ndarray 变量的相关系数矩阵
import numpy as np
vc=[1,2,39,0,8]
vb=[1,2,38,0,8]
print(np.mean(np.multiply((vc-np.mean(vc)),(vb-np.mean(vb))))/(np.std(vb)*np.std(vc)))
#corrcoef得到相关系数矩阵（向量的相似程度）
print(np.corrcoef(vc,vb))

3、表示出“贝叶斯公式”运行逻辑

class Bayes(object):def __init__(self):self._container = dict()def Set(self,hypothis,prob):self._container[hypothis]=probdef Mult(self,hypothis,prob):old_prob = self._container[hypothis]self._container[hypothis] = old_prob*probdef Normalize(self):count = 0for hypothis in self._container.values():count=count+hypothisfor hypothis,prob in self._container.items():self._container[hypothis]=self._container[hypothis]/countdef Prob(self,hypothis):Prob = self._container[hypothis]return Prob
#实例化Bayes类
bayes = Bayes()#先验概率
bayes.Set('Bow_A',0.5)  #P(碗A)=1/2
bayes.Set('Bow_B',0.5)  #P(碗B)=1/2#后验概率
bayes.Mult('Bow_A',0.75)  #P(香草饼|碗A)=3/4
bayes.Mult('Bow_B',0.5)   #P(香草饼|碗B)=1/2bayes.Normalize()
prob = bayes.Prob('Bow_A')#P(碗A|香草饼)
print('从碗A渠道香草曲奇饼的概率:{}'.format(prob))

这篇关于随机事件与随机变量的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---